基于步进电机控制系统复杂动力学研究

姬清华

（新乡学院，新乡 453003）

0 引言

到目前为止，关于步进电机的动力学特性的一些问题尚未得到圆满解决，是因为力矩角度关系的非线性性制约着步进电机动力学的研究。本文根据实际情况采用近似方法,用折线代替步进电机的力矩相角曲线, 在此基础上作出其相迹图, 并根据相迹图提出当步进电机高于其极限频率时的最佳起动方式,并且找到其相应的控制电路和试验结果。

1 步进电机的等值结构图

我们用图1表示步进电机运行的输入和输出关系,其中g(t)表示的是输入量, x (t)表示的是输出量,θ(t)表示的是前两者的差值, 也就是步进电机的输入角度。根据图(1)我们可以写出下面所列的拉普拉斯变换方程式:

这里g0=θm, 一个步距的角度, T为脉冲周期。

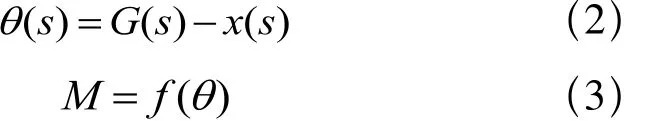
这是步进电机的力矩相角曲线,是一个非线性关系。

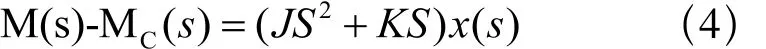
该运动方程式表示的是当步进电机的初始条件等于零时的状态方程[1], 式中MC表示的是静负载, J表示的是转动惯量，K表示的是阻尼系数。根据上面所列的关系式, 我们可以得到如图2所示的结构图 。

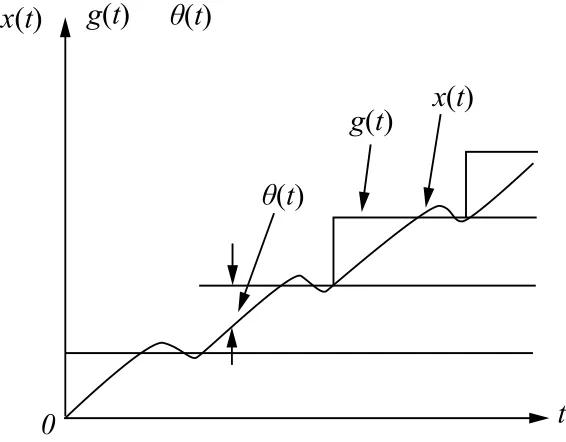
图1 步进电机运行时输入输出关系

图2 步进电机运动方程式结构图

2 步进电机的相迹图

图3表示的是步进电机的力矩相角曲线的非线性关系, 在分析这个问题时,我们用直线1与2来近似表示。在这样的近似的定量计算上我们可以用这种方法近似表示[2], 如果需要比较好的正确度和精确度, 我们近似用三条直线表示, 同样我们也可以推广且应用下面的讨论方法。

直线1与2的方程式如下:

直线2：

实际情况是阻尼系数K是很小的, 可以忽略不计,并且我们假设电流的增长是瞬间完成的, 于是分成下面两种情况讨分析讨论:

1）无干摩擦转矩MC时的情况。

此种情况下, (4)式可以改写成下式

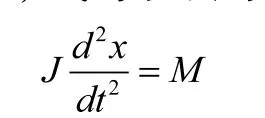
并由于第(2)式的关系, 可以得到

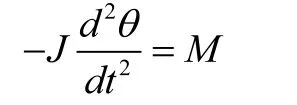
由于直线段l的作用, 可以得到下式

得到相迹方程式如下：

2）存在干摩擦转矩MC时的情况。

这种情况下的相迹方程式如下：

3 步进电机的控制

由上面得到的步进电机的相迹图, 我们就可以借助此来研究对步进电机的控制,控制要求做到下面两个方面：1）过渡过程中要做到不失步。2）快速达到稳定的状态[5]。

在这里我们用起动作为例子进行讨论。

在步进电机的控制过程中首先的是确定控制量,控制量包括脉冲周期T和电流,如果我们变换其中的任一个, 都可以进行控制。步进电机的起动首先是在以2θm为直径的圆上上升的，这个圆我们称之为基本圆, 现在如果假设MC=0 , 如果我们要步进电机稳定运行在这个基本圆上,只要算出脉冲周期T。

但假如输入的脉冲周期恰好是T,一步起动完毕就可以做到, 在第一步时我们使脉冲间隔时间T0可为:

从周期T1开始工作（即第二步）, 这样就可以达到一步起动完华的要求。假如脉冲周期不是T1,能一步起动完毕, 这是因为稳定工作时步进电机的相迹曲线不在基本圆上, 假如要求在这种情况下使其一步起动完毕, 我们可以改变a1, 使a1增加到a1',即变为基本圆, 这样就可以和上面一样达到一步起动完毕的目的。但是因为a1不可能没有限制的增长, 即也就是电流的增长不是无限制的, 其一是磁路饱和, 其二是电机允许发热限制, 也就是说, 电机额定电流以下的情况若要通过改变电流的方法来达到一步起动完毕是受限的, 假如超过了步进电机的额定电流, 以下几步可以帮我们达到稳定的状态，下面我们就讨论这种情况。为使步进电机起动相迹和最后稳定相迹吻合起来，我们可以用改变启动过程中的某些周期，这个方法通过改变电流实现，但是这种方法使的控制系统变得比较复杂。

求出步进电机的起动相迹之后, 我们就可以利用(11)(15)式算出各段时间tab, tch,…, 起动就可以按照这些时间的控制, 等运动到m后,系统就可以稳定的周期TC工作。我们也可以用同样方法处理其他状态过程。

4 实验系统

运用上面所述方法, 计算并试验了实际的步进电机系统，我们采用的是反应式步进电机,该电机有60齿, 他的转动惯量J=1.35克/分米秒2,TL=0.0008秒, 图3表示的是该电机的力矩相角曲线,其类似于直线1和直线2。可以算得a1=108，a2=202 , 当起动电流IC=1安作用在该步进电机上时, 步进电机在脉冲频率小于110时可以直接起动,但当脉冲频率大于110步进电机不能直接起动, 运用本文上面讨论的方法进行起动的话, 步进电机在脉冲频率高于110赫的情况下就可以起动，按照上节的方法, 先画出步进电机的起动相迹图, 起动过程需要四步,第五步步进电机就可以稳定运行。在起动过程中的每一步, 我们可以根据上述相迹图算出,例如电机稳定的工作频率,利用相迹图可以测得其弧度。

我们用x(t)所表示的是反应式步进电机的输出角度,图下部的波形是当时间为秒的标记,图上面表示的是步进电机的输入脉冲,当到达第五步后, 也就是步进电机稳定的频率fc=193赫兹。

图4 在fc=193赫兹时起动过程图

试验结果同时也可以告诉我们, 当频率即使高于193赫兹, 采用上述方法,步进电机也能够很好的起动。

[1] 李宁.运动控制系统[M].北京: 高等教育出版社, 2004.

[2] 潘新民.单片微型计算机使用系统设计[M].北京: 人民日报出版社, 1992.

[3] 沙占友.单片机外围电路设计[M].北京: 电子工业出版社, 2003.

[4] Choi B L, Park J M.An improved rotor model with equivalent dynamiceffects of the support structure.Journal of Sound and Vibration, 2001, 244(4): 569-581

[5] 孙保苍, 周传荣.轴承-转子系统的分岔与混沌特性研究[J].振动、测试与诊断, 2004, 24(3): 192-196.

[6] 童小忠, 吴文健, 林成.镇海发电厂1号汽轮发电机组振动的诊断与处理[J].动力工程, 2000, 20(4).