功率分流式混合驱动系统比较分析

温英科，赵 峰

(1.中国科学院电工研究所，北京 100190;2.中国科学院大学，北京 100080)

自20世纪六七十年代液力机械综合传动大规模应用后，在随后三四十年时间内车辆传动技术没有发生根本性改变.随着以信息化为代表的高新技术革命的发展，混合动力电传动系统的研究开始兴起.现在以信息化为主导、以混合动力电传动技术为基础、以综合电子技术和电气控制技术、主动悬挂技术等为支撑的高机动平台已成为未来混合动力车辆的发展方向.功率分流式混合动力传动系统是最早被提出且获得应用的混合动力车辆电传动系统之一.

1 功率分流式混合驱动系统概述

功率分流式混合驱动系统，是一种带有行星排的功率分流 (耦合)结构，它将发动机和2个发电/电动机通过1个或多个行星排连接 (耦合).它可以实现纯电驱动、混合驱动、机械驱动等多种工作模式，通过调节发电机和电动机的转速实现输出转速的无级变化.功率分流驱动系统以提高车辆燃油经济性为出发点，以电机功率最小为目标，通过机械和电力的有机复合，来降低系统对电机容量的需求，提高系统经济性.

功率分流混合驱动系统的优势有2点:1)发动机的能量可以直接传递给负载，避免了能量在中转过程中出现的能量损耗:2)发动机的转速和扭矩与车轮的转速和扭矩解耦后，发动机可以工作在较小范围的经济区内，使系统的燃油消耗达到最优[1].

比较有代表性的功率分流混合驱动系统有单模式混合驱动系统、双模式混合驱动系统和四模式混合驱动系统.

2 单模式功率分流混合驱动系统

图1为单模式功率分流混合驱动系统结构图[2].单模式混合动力系统包含2台电机 MC1、MC2和2个行星排PG1、PG2.

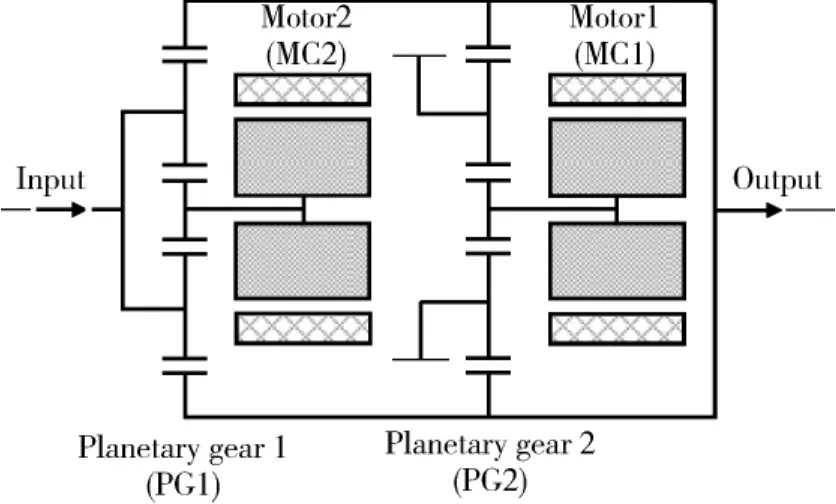
图1 单模式功率分流混合驱动系统

当系统工作时，发动机发出的功率经过PG1分流一部分通过纯机械路径直接传递到输出轴;另一部分通过电-机械路径，先流经发电机转化为电能再驱动电动机转化为机械能带动车辆工作，后者称为中转功率.电机MC1通过PG2与输出轴相连，不影响系统输出转速.系统输出转速由发动机转速和电机MC2转速决定，系统输出扭矩由2个电机输出扭矩共同决定.定义中转功率与发动机发出的总功率的比值为中转功率比PR，它反映了在满足系统动力输出的前提下，系统所需电机功率的大小.假定纯机械路径系统效率为100%，所有的能量损耗都发生在能量的转换过程中，因此PR还被用来表征系统的经济性.在设计中希望系统的PR越小越好，以降低系统对电机容量的需求，提高系统的效率.定义发动机转速与主减速器前的系统输出转速之比为系统速比SR.

列写2个行星排特征方程[3]:

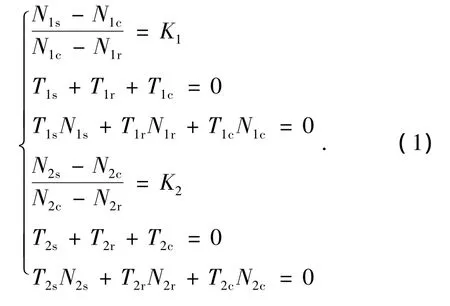
根据连接关系有:

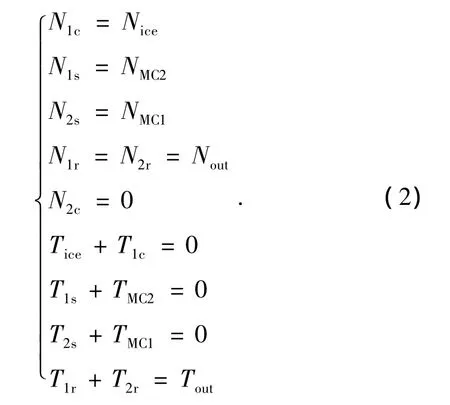
联立式(1)和式(2)，解得:

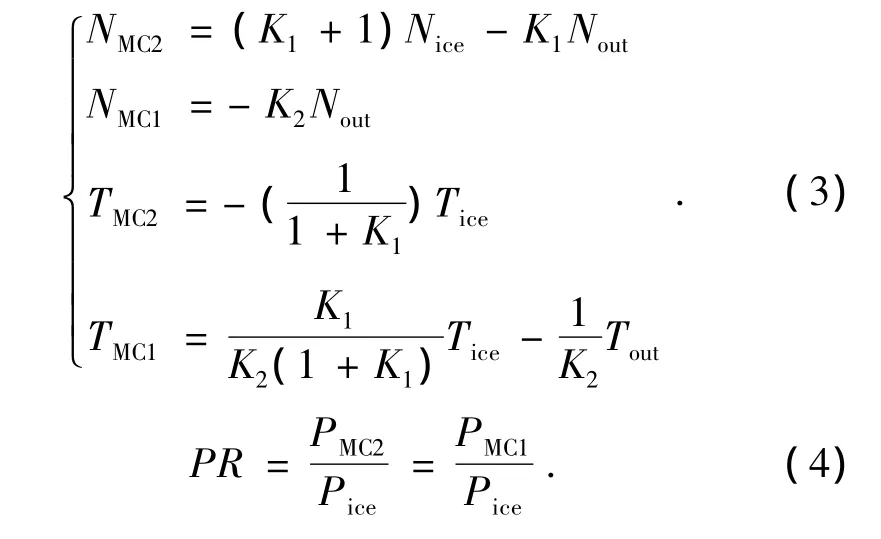
联立式(3)和式(4)，可得系统PR和SR有如下关系:

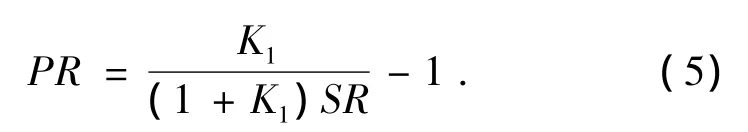
式中:Nix为第i个行星排太阳轮、行星架和外齿圈的转速;Tix为第i个行星排太阳轮、行星架和外齿圈的扭矩;Nice为发动机转速;Tice为发动机扭矩;NMCi为第i个电机的转速;TMCi为第i个电机的扭矩;Nout为系统输出转速;Tout为系统输出扭矩;Ki为第i个行星排特征参数，即行星排外齿圈与太阳轮的齿比;i=1，2;x=s，c，r.

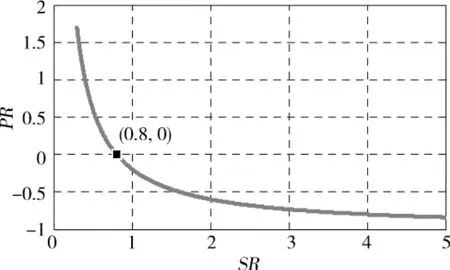
图2 单模式系统功率特性

给定K1=4时，将式(5)表示成曲线的形式如图2所示.当SR=0.8时，PR=0，此时所有发动机发出的功率都通过纯机械路径传递到输出轴，系统的效率最高，依据之前的假设可以认为这时的系统效率为1，定义系统效率为1的点为系统的机械点.在0.8的基础上，随着SR逐渐增大或减小，PR的绝对值逐渐增大，这时有越来越多的功率通过电-机械路径传递到输出轴，由于能量在中转过程中的损耗，随着PR绝对值的增大系统效率也逐渐降低.

混合驱动系统可达到的最大速比与最小速比之比称为系统的变比.对某一给定PR最大值 (绝对值最大)，可与图2所示曲线交于两点，两点横坐标之比，即在给定PR最大值下系统的变比.令PR=±a，则有:

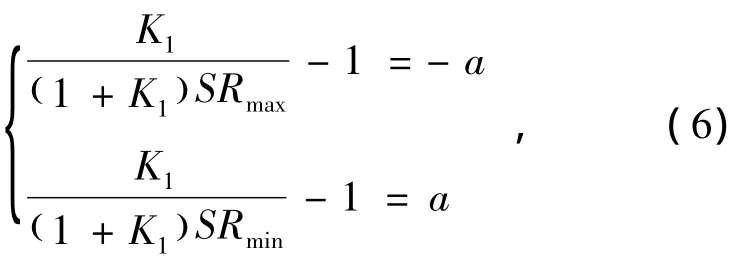
解得:

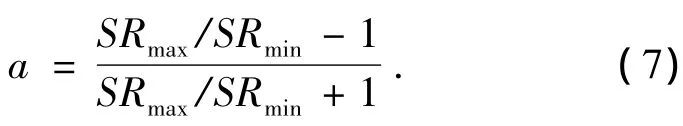
式中:SRmax为系统最大速比;SRmin为系统最小速比.

可见单模式系统PR的最大值，即系统对电机容量的需求，是系统变比的单值函数，随系统变比的增加而增大，变化趋势如图3所示.即当系统变比选定时系统需求的电机功率随之确定，与系统中行星齿轮特征参数无关，因此在设计时无需进行行星齿轮特征参数的优化.

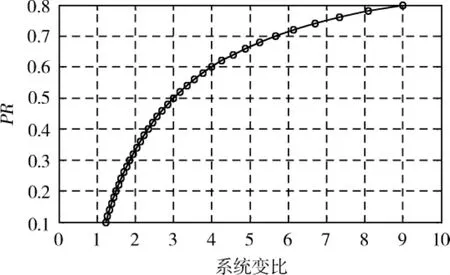
图3 单模式系统最大中转功率比随系统变比的变化

3 双模式功率分流混合驱动系统

图4为双模式功率分流混合驱动系统结构图[2]，包含 2台电机 MC1、MC2和 2个行星排PG1、PG2，与单模式系统的不同之处在于双模式系统增加了一个锁止器CL1和一个离合器CL2.系统通过CL1和CL2的开关动作实现2种不同模式的转变，如表1所示.

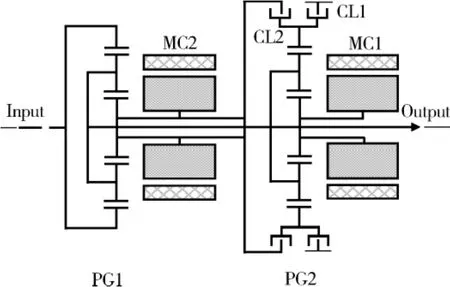
图4 双模式功率分流混合驱动系统

表1 双模式混合驱动系统工作模式

给定一组行星排特征参数可画出如图5所示的双模式混合驱动系统在各模式下PR随SR的变化规律.2种模式下的功率特性曲线大致相交于SR=1.7的位置.为使系统在整个速比范围内都保持较高的经济性，在各速比点系统应工作于PR相对较小的工作模式，因此，对于此双模式混合驱动系统而言，当系统速比大于1.7时，应当工作于MODE1;当系统速比小于1.7时，应当工作于MODE2.当系统速比连续变化时模式的变化以及系统整体功率特性如图6所示.可见相对于单模式混合驱动系统，双模式系统由于工作模式的增加，使系统PR在相对较宽的速比范围内保持在较低的数值，降低了系统对电机容量的需求，提高了系统的经济性.

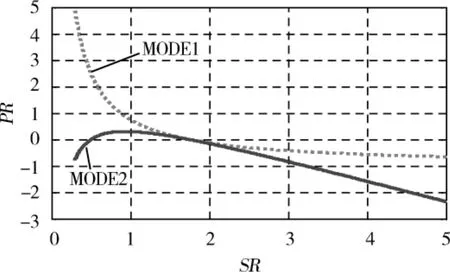
图5 双模式系统各模式功率特性

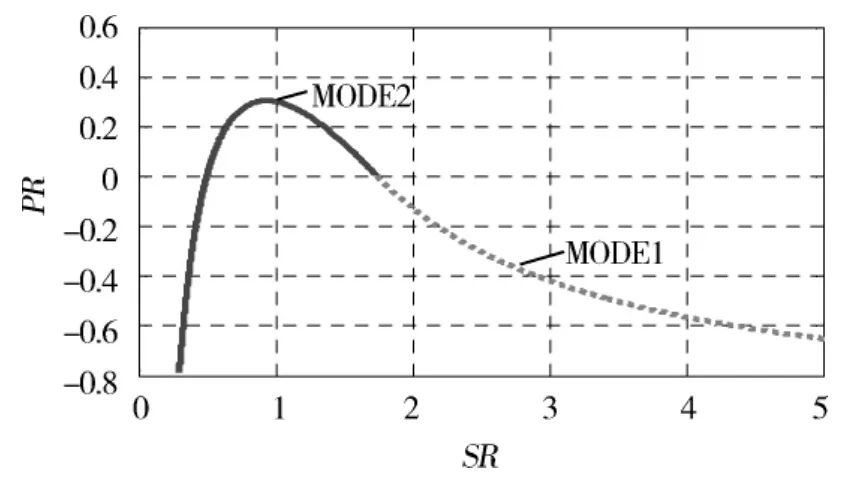
图6 双模式系统模式的变化

如图6所示，双模式混合动力系统PR随SR的变化是一条非单调曲线，在MODE2时达到极值点作为系统PR的最大值，记为a，相应地当PR=-a时，可与曲线交于两点，两点横坐标之比即系统变比.系统PR最大值以及变比都是K1，K2的函数.双模式混合动力系统对电机功率的需求由系统变比和系统中2个行星齿轮的特征参数共同决定.系统对电机功率的需求随系统变比的增加而增大，变化趋势如图7所示.当系统变比确定时总可以找到一组最优的K值使系统对电机功率需求最小，即在设计时需要进行系统行星齿轮特征参数的优化，这个过程可以借助于MATLAB中求解非线性约束最优化问题的fmincon函数进行求解.以系统最大PR值最小为优化目标，以给定的系统变比为约束条件，求解非线性约束最优化问题.当系统变比选定为6.5时，有:

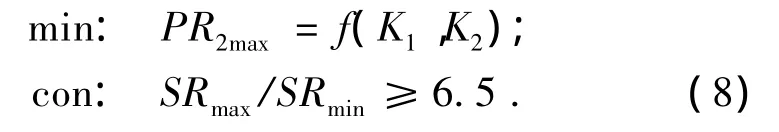
式中:PR2max为MODE2中转功率比的最大值.

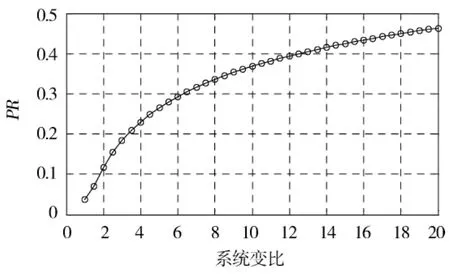
图7 双模式系统最大中转功率比随系统变比的变化

需要注意的是，当给定某一变比并完成K值优化后，需对车辆的输出能力进行校核，如不能够满足车辆动力性能指标，则需增大系统变比，重复上面的K值优化过程，此时系统电机的容量也会随之增大，系统整体经济性将会降低.

4 四模式功率分流混合驱动系统

图8为四模式功率分流混合驱动系统结构图[2]，包含 2个电机 MC1、MC2;3个行星排PG1、PG2、PG3，其中PG1、PG2为单级行星排，PG3为双级行星排[4];2个锁止器 CL1、CL3和2个离合器CL2、CL4.系统通过离合器和锁止器的开关动作来实现4种不同模式的转变，如表1所示.

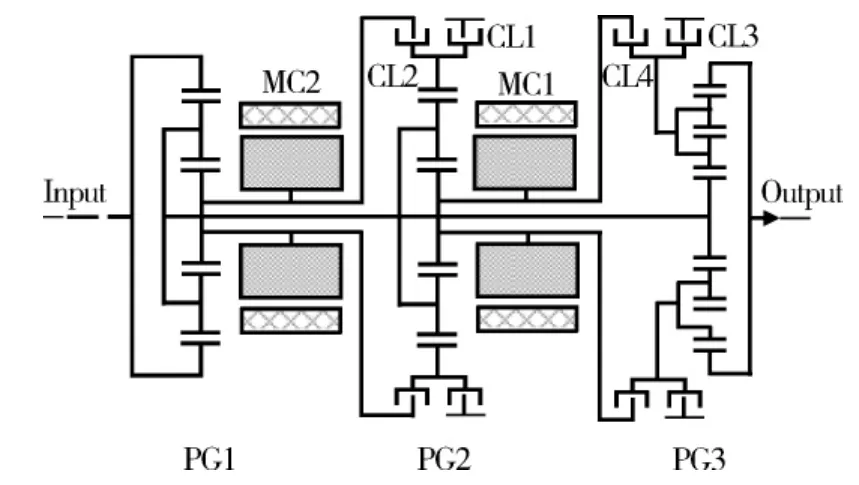
图8 四模式功率分流混合驱动系统

表2 四模式混合驱动系统工作模式

同双模式混合动力系统的原理相同，四模式混合驱动系统也是通过不同模式的转换使系统PR在较宽的速比范围内保持在较低水平，从而使尽可能多的能量通过纯机械路径传递到输出轴，降低能量损耗，提高系统的经济性.

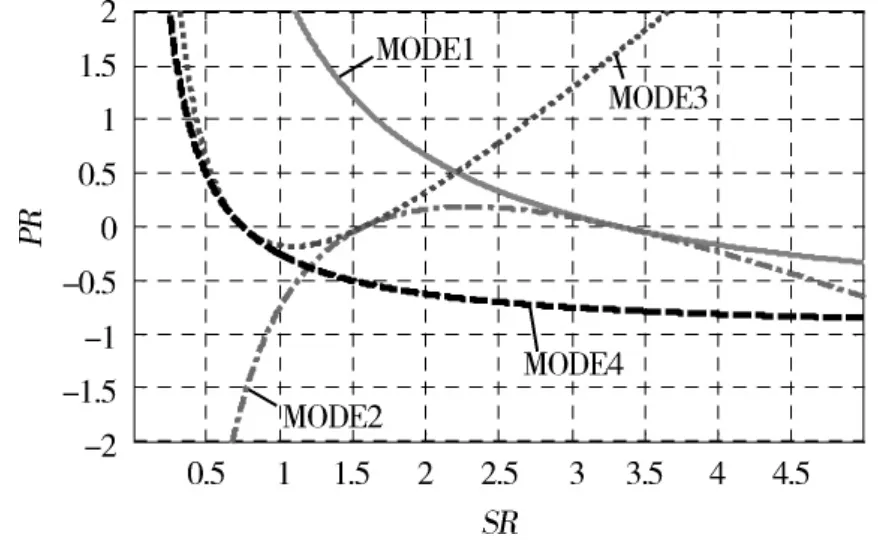
图9 四模式系统各模式功率特性

给定一组行星排特征参数可画出如图9所示的四模式混合驱动系统在各模式下PR随SR的变化规律.以MODE2为例，由图9可见:当系统SR在1.5～3.5之间变化时，系统PR值较小，此时系统大部分能量通过纯机械路径传递到输出轴;而当SR的数值小于1.5或者大于3.5时，系统PR值迅速增大，此时，发动机发出的很大一部分功率经过2个电机进行能量转换后传递给输出轴，这就造成能量的损耗，使系统经济性急剧降低.因此当SR的数值小于1.5或者大于3.5时，MODE2不再适用.对于其余3种工作模式都有相似的工作特性，即都是在一定的速比范围内能将系统效率维持在一个较高的水平，超出这一速比范围系统效率急剧降低.取各速比段中PR最小的模式为相应速比段的工作模式，可得到，随着速比的减小，由右向左系统应当依次工作于 MODE1、MODE2、MODE3和MODE4模式，4个模式的曲线彼此相连如图10所示.需要指明，由于MODE4的曲线随SR变化过于剧烈，经济性不佳，因此四模式混合动力系统很少工作于第4种模式.

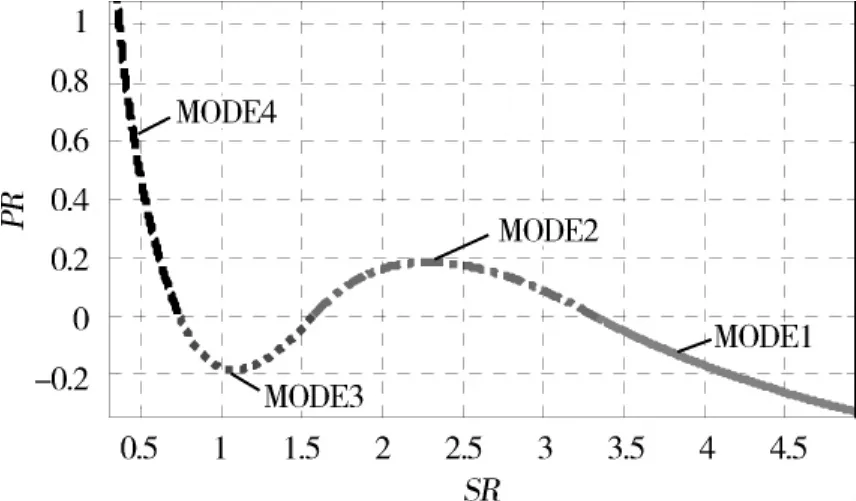
图10 四模式系统模式的变化

四模式混合动力系统PR随SR的变化也是一条非单调曲线，在MODE2、MODE3时达到极值点，分析时需讨论两极值点的大小.选定极值点后与MODE1、MODE4曲线交于两点，两点横坐标之比为系统变比.系统PR最大值以及变比都是K1，K2，K3的函数.系统对电机功率的需求由系统变比和系统中各行星齿轮的特征参数共同决定.系统对电机功率的需求随系统变比的增加而增大，变化趋势如图11所示.与双模式系统相同，当四模式系统变比确定时总可以找到一组最优的K值使系统对电机功率需求最小，四模式系统在设计时也需要进行系统行星齿轮特征参数的优化，同样借助fmincon函数进行求解.以系统PR值最小为优化目标，以选定的系统变比为约束条件，求解非线性约束最优化问题.

为满足车辆动力性能指标，给定系统变比后，同样需要对系统的动力输出性能进行校核.

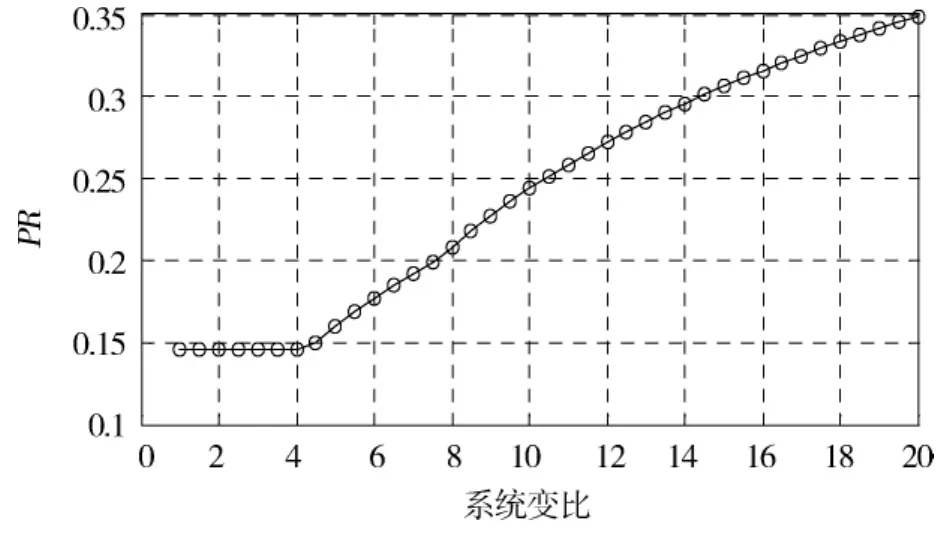
图11 四模式系统最大中转功率比随系统变比的变化

5 3种结构比较

为方便对3种结构的经济性和各自对电机功率的需求进行对比，将图3、图7、图11的曲线画于一张图内，如图12所示.

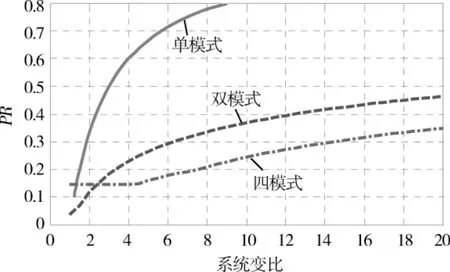
图12 3种结构PR最大值随系统变比变化趋势对比

从图中可以明显看出:当系统变比大于2.5时，在同一系统变比下单模式系统、双模式系统以及四模式系统PR最大值依次降低.可见随着工作模式的增加，系统对电机容量的需求逐渐降低，系统经济性逐步提高，但与此同时车辆传动系统的复杂性和控制的难度也随之增加.

在实际应用中，丰田Prius采用单模式混合驱动系统，第二代Prius动力系统由1.5 L、57 kW发动机和50 kW电动机构成，电动机功率为发动机功率的87.7%;第三代Prius动力系统由1.8 L、73 kW发动机和59 kW电动机构成，电动机功率为发动机功率的80.8%.GM采用的是双模式混合驱动系统，其推出的GMC Yukon混合动力车的动力系统采用6.0 L、237 kW汽油型发动机搭配60 kW电机，电机功率为发动机功率的25.3%.可见，通过增加模式可以大幅度降低电机的容量，从而减小系统体积，但是会增加离合器和锁止器，增加控制的复杂程度，在实际应用中需要根据实际情况选取.

6 结论

通过对单模式、双模式以及四模式功率分流混合驱动系统工作原理，及其结构的对比分析，得出如下结论:

单模式混合驱动系统结构简单，控制较容易，成本较低;但对电机功率要求高，系统电机体积大，且经济性不佳.适用于低功率、对系统变比和经济性要求不高的小型混合动力车辆，如丰田Prius采用的就是这种混合动力系统.

四模式混合驱动系统通过多种模式的转换，大幅降低了系统对电机功率的需求，实现了电机小型化，节约了空间，系统经济性好;但传动系统结构复杂，控制难度大，成本较高.适用于高功率、对系统变比要求较高的中重型车辆.如将四模式系统运用于低功率车辆，虽然可以适当降低电机系统的体积，但四模式系统本身增加的4个离合器同样占用了较大的空间，整个传动系统在体积上可能反而会增大，因此四模式系统对低功率小型车辆并不适用.

双模式混合驱动系统对电机功率的要求、系统经济性、控制的复杂程度以及成本介于单模式和四模式之间，适用于性能要求较高的混合动力车辆.现通用、宝马、戴克集团已联手开发了双模式混合驱动系统的车型，其电机系统体积只有普通单模式混合动力系统的一半左右，在保证车辆高性能的同时进一步优化了燃油经济性.

[1]项昌乐，韩立金，刘 辉，等.混联混合动力车辆功率分流耦合机构特性分析 [J].汽车工程，2010，32(3):183-187.

[2]Namdoo Kim，Jason Kwon，Aymeric Rousseau.Tradeoff between Multi-mode Powertrain Complexity and Fuel Consumption[C].//The 25th World Battery，Hybrid and Fuel Cell Electric Vehicle Symposium＆Exhibition.Shenzhen，China.2010.

[3]饶振纲.行星齿轮传动设计 [M].北京:化学工业出版社，2003.

[4]李兴华，黄宗益，张承航.三自由度行星变速器传动方案设计 [J].中国机械工程，2002，13(20):1727-1729.