ARV 路径跟踪控制算法研究

姚其昌，卢国轩，蓝 伟

(中国北方车辆研究所，北京 100072)

路径跟踪控制是指移动机器人沿着给定的与时间无关的几何路径进行移动控制的过程.路径跟踪控制的基本思想是先求出轨迹目标值和车体位姿的偏差，随后根据获得的偏差量，产生一个相应的控制命令，并发送给移动机器人的控制系统，使其偏差逐渐减小.路径跟踪问题有不同的数学描述方法，比较普遍并得到广泛认同的提法为:对于任意给定的几何路径 f(x，y)=0，寻找反馈控制律u=u(x，y，φ)，使受控移动机器人最终能沿着期望的几何路径运动，即对于任意给定的ε＞0，有f(x，y，φ)＜ ε[1].

早期移动机器人路径跟踪控制是使动力学模型在目标路径附近线性化，这种方法虽然计算简单，但由于局部线性化不能保证系统的全局稳定，而采用反馈线性化方法可完全补偿机器人的非线性.Kanayam YJ在文献[2]和[3]中将利用移动机器人的路径曲率的微分表示曲率、位置误差、姿态误差的线性组合形式，称为“操纵函数 (Steering Function)”，并取位置误差、位置误差的一次微分、位置误差的二次微分作为变量，使控制系统线性化[2-3];Zhong-Ping Jiang等利用链式系统采用反推技术实现跟踪[4];变结构控制不需要知道系统精确的数学模型，当系统进入滑动模态后，对系统干扰和参数变化具有完全的自适应性;文献[5]采用滑模控制，使路径跟踪控制具有很好鲁棒性的控制律[5].

本文研究的移动机器人为武装机器人车辆(Armed Robot Vehicle即ARV)，其路径跟踪控制属于非完整控制系统的范畴.为了达到良好的路径跟踪控制效果，首先利用ARV参考路径的曲率、车体相对于参考路径的偏航角以及位置偏移量等变量参数建立运动学模型，然后利用链式系统把非线性运动学模型线性化，从而实现与速度无关的路径跟踪控制.

1 ARV运动学模型

1.1 模型假设

为了推导可用于控制器设计的ARV运动学模型，需要做出如下的平衡:

1)模型必须能够很好地反映ARV的行为，但是其复杂程度要受到控制器设计要求的限制;

2)从控制器设计的角度建立的简单运动学模型能够较好地反映ARV的行为.

因此，模型在建立的过程中遵循以下假设:

ARV及其车载部件为单一的刚体，因此把其描述为双轮车模型 (即Ackermann’s模型):前中轴都用虚拟的单轮所代替，后轴作为车体刚体的一部分，其转向轮转角根据前轴转向轮的转角由几何关系换算获得，如图1所示，虚拟轮位于实际轮子的中间位置.在不考虑滑移的情况下，这个假设在移动机器人领域中普遍应用[6].

图1 车体简化模型

本研究的控制目标为路径跟踪，因此结合相对参考路径C而不是绝对参考路径描述车体构型.如图1所示.各参数的意义是:

C为所跟随的路径，定义在绝对坐标系XAAYA下;

O为车体虚拟中轮的中心 (即车体中轴的中心);

M为C上距离O点最近的点，假设点M是唯一的.实际上，一方面由于ARV总是接近C，另一方面路径C的曲率很小，因此这个假设是合理的;

s为点M沿路径C曲线的横坐标，c(s)为路径C在该点的曲率，θc(s)为C上该点的切线在坐标系XAAYA下的方位角;

θt为ARV的中心线在坐标系XAAYA下的方位角.因此θ=θt-θc(s)为ARV相对于路径C的偏转角;

y为ARV相对于路径C的横向偏移距离;

υ为ARV在点O的线性速度;

δ为前轮相对于ARV中心线的方位角;

l为中前轮轮距.

由于把ARV及其车载部件作为一个刚体，根据车体中心线的方位角以及车体上任意一点的位置(比如点O)便可以得出车体的总体构型.而这2个参数信息可以由(s，y)这一对参数和变量θ来代替，因此车辆的状态变量可以写成:

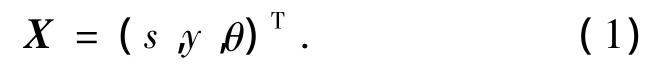
作为路径跟踪控制的运动学模型，ARV车辆控制状态变量为:

由式(1)、式(2)便得出了考虑两轮与地面持续相接触的车辆状态空间模型.

1.2 车辆运动学模型

假设ARV在运动过程中车轮只发生纯滚动而没有滑转，这说明车轮中心点线速度矢量在轮面上.把此假设应用于图1所示的双轮车模型，便可以得到双轮车模型中前两轮的速度以及前轮转向角度.

考虑到把整个车体作为一个刚体，在任意时刻，车体的运动分为两种:纯粹的平移运动和绕某一瞬时转向中心点IRC的转动.实际上，这两种情况可以归为一种情况，平移运动其实就是瞬时转向中心点在无穷远处的特殊转动.当车体做纯滚动时，IRC可以由车体任意两点线速度矢量垂线的交点确定;当车体做平移运动时，任意两点线速度矢量相互平行，IRC在无穷远处.如图2所示.

图2 车体角速度的示意图

图2中，IRC由点O和前轮中心点速度矢量垂线的交点确定.此处定义d为IRC和点O的距离.车体的绝对角速度˙θt便可以得出，即

d的值可以通过公式 (4)得出.

因此由式(3)和式(4)可以得出:

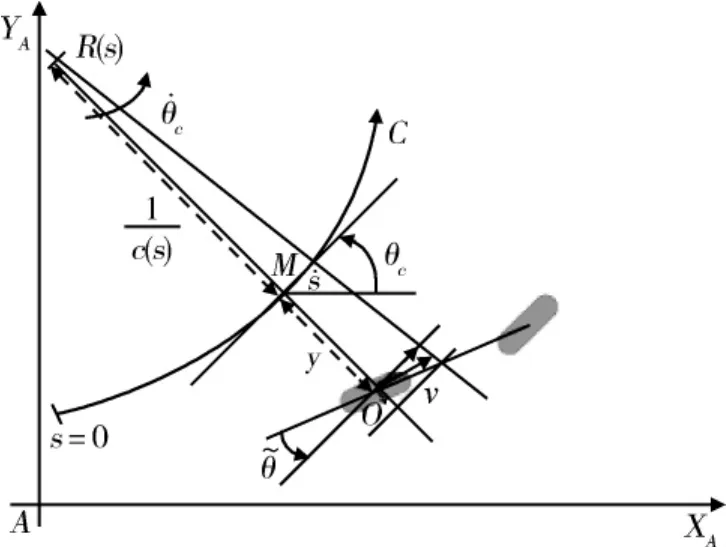
图3 车体偏移角速度的示意图

其中，y在图3中为负值，因此在式(6)中为减号.从式(6)中可以得出:

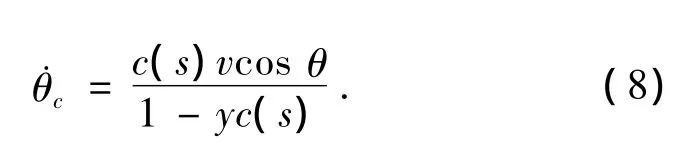
从图3中还可以得到:

注意到图3中θ为负值，式(9)中的符号与此相一致.当轮地接触符合纯滚动无滑转的假设时，式(5)、式(7)～式(9)为我们提供了最终的车辆运动学模型，即

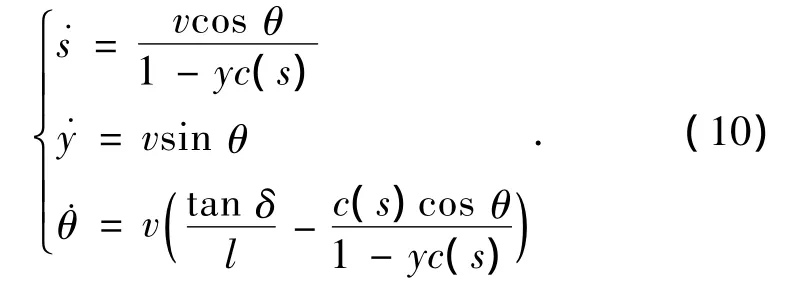
2 ARV控制算法

控制算法开发的目的是保证ARV能够较好地跟随路径C，即要求状态变量y=0，θ=0.y=0意味着ARV车辆在规划路径C上，θ=0意味着车辆方位角变化与路径C切线方向的变化相一致.在不考虑滑转的情况下，车辆运动模型可以由式(10)来描述，这个模型很明显为非线性模型.运用现代控制理论已经可以把移动机器人模型转换为线性模型，即链式模型[7]，具体细节见文献[7].这种方法可以把实际非线性车辆模型使用线性系统理论方法求解.

转换为两输入链式方程的非线性模型一般写成如下的形式[7]:

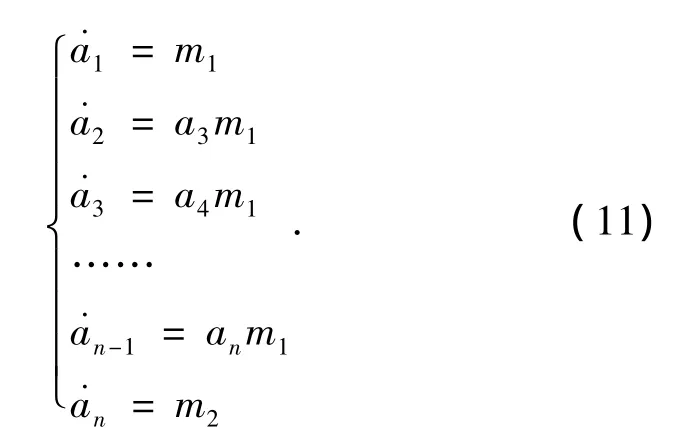
设 A=(a1，a2，…an)T和 M=(m1，m2)T分别为状态向量和控制向量.

为了保证链式方程基本上为线性系统，用各状态变量对a1的导数代替其对时间的导数，即:

则链式方程式(11)可以写成:

式(13)中前n-1个等式很明显为线性系统.

把ARV车辆模型式(10)转换为链式方程.当维数为3时，通用的链式系统式(11)和式(13)可以写成如下形式:

对时间的导数:

对a1的导数:

为了使所设计的控制器性能不受车速的影响，状态变量a1可以设为:

式(16)作为起始设定值，把其代入式(14)或式(15)即可把非线性车辆模型转换为链式方程.

为了符合式(14)的形式，新的控制量m1可以定义为:

为了简化模型，可以尝试a2=y，同时设定˙a2=vsin θ≜a3m1.

因而最后一个状态变量a3只能为

最终，可以得出最后一个控制变量m2为:

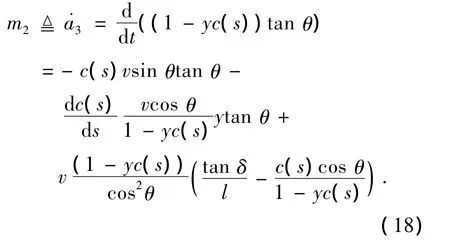
通过上面的变换，非线性ARV运动学模型式(10)转换为链式(14)或式(15)的形式，其状态变换为:

式中:Ψ(X)=(s，y，(1-yc(s))tan θ)T.

控制变量转换为:

3 ARV路径跟踪控制的实现

有了上面的链式模型，控制器便可以很容易地设计出来.由于链式系统式(15)为线性系统，虚拟控制律可以很自然地描述为:

实际上，把式(21)代入式(15)可以得到:

上式说明a2能够收敛于零，根据式(19)，y收敛于0就保证路径跟踪的目标得以实现.同时，a2收敛说明a3也收敛(可参见链式方程式(15)).状态变换式(19)也保证了角度偏差θ也收敛于0.

由于误差动态方程式(22)基于a1=s(Kd，Kp)为距离的增益量而不是时间的增益量，因而，对于给定的初始误差，不管车体的速度是多少或者车体速度是否随时间发生变化，车体的轨迹都是一样的.即从控制器设计的角度来看，路径跟踪的效果与速度无关，控制律增益与车速无关.实际上，理论结果或许有稍微的变化，这是由于θt(因而影响到θ)的测量值很明显受到车速的影响 (参见式(5));另一方面，车载传感器并不是完全线性的.但是，考虑到车体的速度范围为0～15 km/h，并限制控制增益(Kd，Kp)的值不至于高到使执行器饱和的程度.

通过变换得到的式(20)就是实际的控制律 (把式(12)、式(17)和式(18)代入式(21)):

可以看到，在控制器的设计过程中没有引入近似值，这就保证了非线性控制律式(23)能够获得精确的曲线路径跟随效果:非线性模型式(10)和参考路径曲率c(s)都在控制律中明确地表达出来.此外，非线性控制律式(23)的性能调节也非常容易，因为它仅仅依赖于线性误差方程式(22)，通过调节增益量(Kd，Kp)可以很直观地获得所期望的距离值.

在实际应用中，参考路径C通常为直线，即c(s)=0，因此控制律式(23)就变得非常简单.

最后，讨论一下执行器饱和的问题.在式(23)或者式(24)中，反正切函数的参数是无界的，而转向轮转向角度被限制在±45°的范围，因此可能发生执行器饱和的问题.处理这个问题的基本方法是调节控制器的性能 (如调节增益量Kd，Kp)，从而使预定的控制操作不会遇到饱和.需要指出的是，执行器饱和不会阻止车体收敛于参考路径C，即使从理论的角度上也可以看出:由于链式模型式(15)包含一个二重积分器，即使式(21)中的m3为任意数，都可以保证其渐进稳定性，参见文献[8].控制性能的唯一缺点就是当执行器饱和的时候，控制律就不再与速度无关.

实际上，转向执行器的最主要问题不是饱和，而是导航闭环控制中所引入的延迟问题.这种延迟所带来的影响在出现滑移的情况下可以很明显地感觉出来.

4 仿真分析

采用Matlab仿真环境分别仿真在不同车速下阶跃响应的控制效果、跟踪正弦曲线的控制效果.

4.1 不同速度下的阶跃响应

参考路径为2 m的阶跃响应，速度从2 km/h加速到14 km/h，每个档次提升2 km/h.在进行仿真的时候需要首先调节(Kd，Kp)的值以获得较好的性能，同时使转向电机不至于饱和 (实际仿真时，Kd=0.6，Kp=0.09).仿真结果如图4所示，可以看出所有不同速度下的阶跃响应曲线几乎全重合在一起，因此可以得出路径跟踪算法和车速无关.

同时还可以看出，除了两端的速度，即速度为2 km/h或14 km/h时路径跟踪的偏差稍微大一些之外，其它速度的路径跟踪效果非常好 (车体轨迹和参考路径之间的偏差小于2.7 cm).

图4 不同车速下的阶跃响应曲线

4.2 曲线路径跟踪仿真

此处选用正弦曲线作为路径跟踪的参考路径，虽然在ARV实际应用场合很少遇到正弦曲线路线，但由于正弦曲线明显不同于直线，因此用于验证路径跟踪控制律式(23)的性能具有很好的代表性.

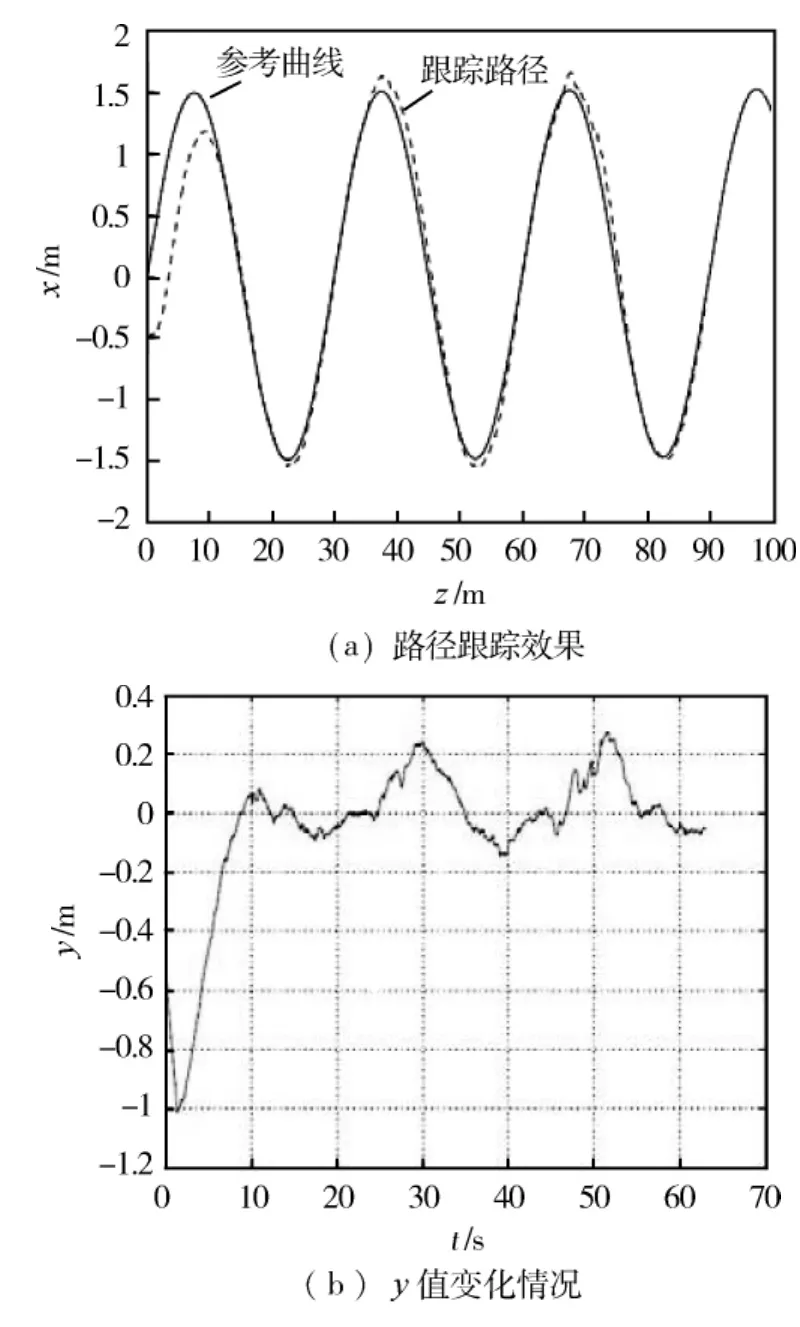
图5 参考路径为正弦曲线时的路径跟踪结果

参考正弦曲线路径的振幅为3 m，周期为30 m，初始时刻，车体距离参考曲线的距离为0.5 m，速度为6 km/h，路径跟踪效果如图5所示.图 (b)给出了侧向偏移y值的变化情况:从总体上来说，侧向偏移被控制在25 cm之内，较好地完成了控制器设计的目标;同时可以看到侧向偏移周期性地出现一个最大值 (大于20 cm).结合图 (a)可以看出，出现最大值的地方为正弦曲线的波峰处，这是由于正弦曲线波峰处，ARV运动学模型 (式(10))的非线性化更加厉害，而控制律 (式(23))从这个模型中演化过来，微小的模型变化或者标定错误都能降低控制器的性能.

5 结束语

推导出了适用于ARV无人车路径跟踪控制的运动学模型，并应用“链式系统”控制理论设计出与速度无关的控制律，通过仿真分析表明该控制律具有良好的控制效果.

在推导运动学模型时，采用了两轮车模型，而实际车辆的瞬时转向中心不一定落在中间车轮的法线上，考虑到滑移的影响，可以通过控制后轮的转向角度以减小滑转，同时本控制算法仅仅考虑了0～15 km/h的速度范围，如果车速进一步提高，就需要考虑侧滑及滑转的影响，甚至需要考虑动力学因素.

[1]王学先，霍 伟.移动机器人路径跟踪的控制研究[D].北京:北京航空航天大学，2002.

[2]Kannayama YJ，Fahroo f.A new line tracking method for nonholonomic vehicles[C].//IEEE International Conference on Rbotics and Autonation. 1997:2908-2913.

[3]Kannayama YJ，Fahroo f.A circle tracking method for nonholonomic vehicles [J].Robot Control，1997，(2)，531-538.

[4]Zhong-ping Jiang， Henk Nijmeijer. A recursive technique for tracking control of nonholonomic systems in chained form [J].IEEE Transactions on Automatic Control，1999，44(2):265-279.

[5]Shim H S，Kim J H，Koh K.Variable structure control of nonholonomic wheeled mobile robot[C].//IEEE International Conference on Robotics and Automation.1995:1694-1699.

[6]C.Canudas de Wit，B.Siciliano，G.Bastin editors.Theory of robot control [M]. Springer-Verlag，Berlin，1996.

[7]C.Samson.Control of chained systems application to path following and time varying point stabilization of mobile robots[J].IEEE Transactions on Automatic Control，1995，40(1):64-77.

[8]H.Sussmann，E.Sontag，and Y.Yang.A general result on the stabilization oflinearsystemsusing bounded controls[J].IEEE Transactions on Automatic Control，1994，39(12):2411-2425.