对图形学算法的改进

胡树杰

（沈阳理工大学 信息科学与工程学院，沈阳 110168）

0 引言

计算机图形学的基础算法一般在工具软件中会被无数次调用，其执行速度是至关重要的，所以它的生成算法的优劣对整个图形系统效率的影响非常大。因此，对一些基础算法的改进，使其进一步完善是必要的。

在计算机图形学的领域中，圆的生成算法比较成熟，经典的单点算法有多种，其中比较熟悉的有Bresenham算法等。本论文对圆的生成算法进行了研究和探索。首先，通过对Bresenham算法画圆算法进行分析，在像素点的选取上进行创新，通过新算法画出的圆比Bresenham画圆法画出的圆更接近真实的圆；其次，新算法的基础上，实现双步画圆，算法的效率的得到最大的提高；第三，对新算法与Bresenham在精度与速度上进行比较，结果显示新算法比Bresenham有很大的优势。

另外，在圆的生成过程中，仅需生成一个八分之一圆，那么圆的其它部分就可以通过一系列的简单反射变换得到。

1 基本思想

通过分析Bresenham画圆算法我们会发现，算法的主要计算量是在对判断变量△d的计算上。本文也定义变量△d为判断变量。

如图1所示，假设P0（x0，y0）点为当前点，为了最佳逼近该圆，根据圆弧的走向，下一点像素的取法只能是正右方像素和右下方像素两种选择，即下一点在 P1（x1，y1）和 P2（x2，y2）两个点中选取一个。P1点和P2点究竟选取哪个点作为下一步的主要取决于这两个点到圆周的距离更小。

2 算法推导

2.1 点的选取

以P1（x1，y1）为基准坐标，则P0的坐标为P0（x1-1, y1），P2的坐标为 P2（x1，y1-1），于是判断公式表示为：

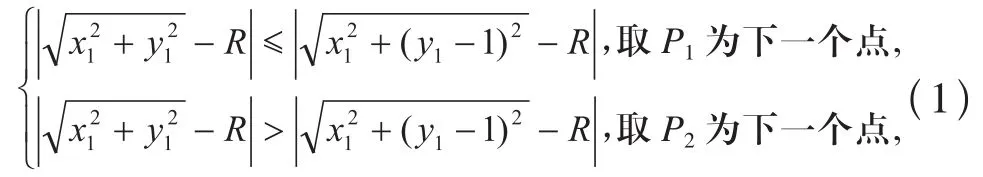
上面这个公式可以判断哪一点是离圆周最近的点，即应该选取的点。

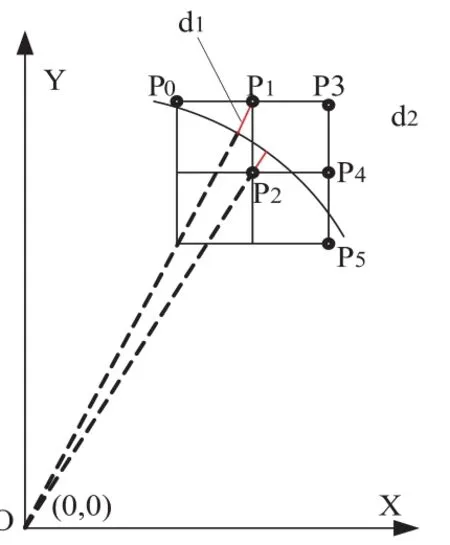
图1 算法示意图

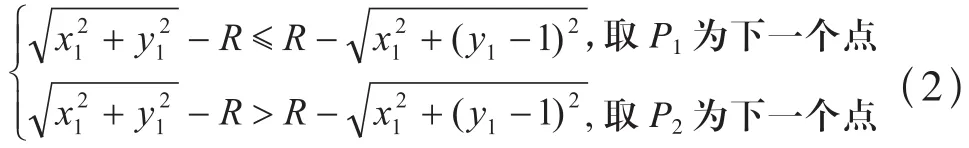
根据公式（2）可以进一步化简为：

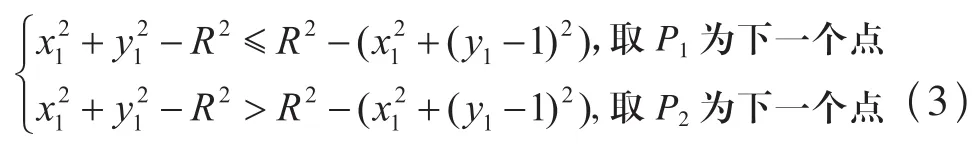
继续化简可得：

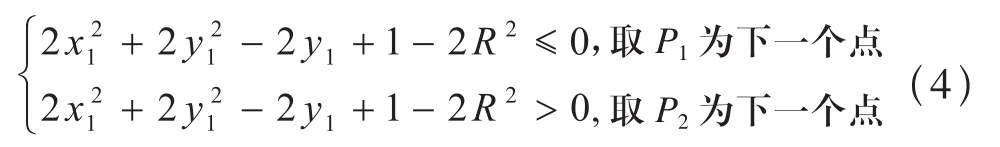
根据公式（4）可以判断出究竟下一点的选取是P1还是P2。令：

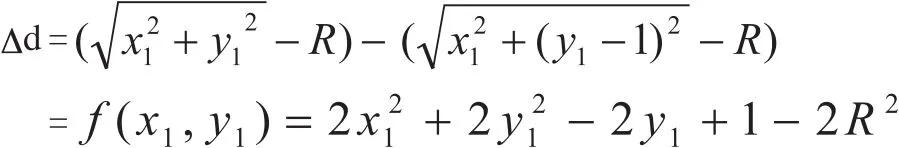
为了简化计算，可以归纳f (x, y)的递推公式。即根据待确定的两个点的上一个点就可以确定这两个点中到底选取哪个点作为所需要画的点。

即令

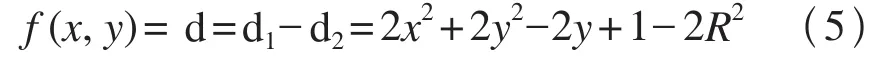
可得以下结论：

当f (x, y)＞0时，下一点取P2；

当f (x, y)＜0时，下一点取P1；

当f (x, y)＝0时，下一点取P1或P2。

则f (x, y)的符号，就可以判断横坐标x对应的点的选取。

若f (x, y)≤0取P1为下一个像素点，则再下一点为P3和P4中的一个，根据判别式可得

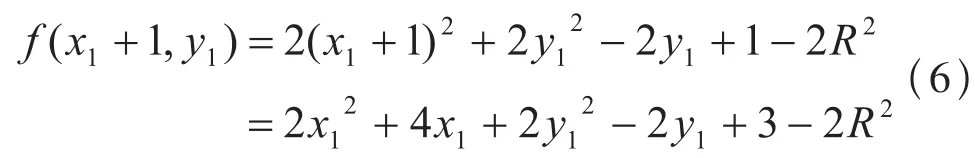
当则f (x1, y1)≤0时选定P1，再根据公式（6）判断出下一点是P3或是P4。

若f (x1, y1)＞0时选定P2，为x坐标对应的点，则下一点的选取在P4(x1+1, y1-1)和P5(x1+1, y1-2)中来选取一个。

再根据公式（5）导出公式（7），即已知选定P2后，继续在P4，P5中选取下一个像素点的公式：

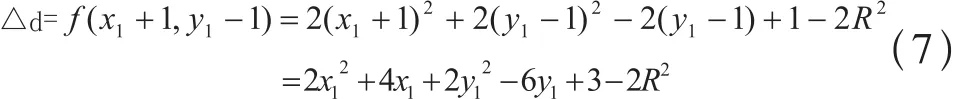
当 d＞0时，下一点取P5为画圆向下进行的像素点；

当 d＜0时，下一点取P4为画圆向下进行的像素点；

当 d＝0时，下一点取P4或P5为画圆向下进行的像素点。

通过以上推导，对Bresenham算法进行了改进。使计算避免了复杂的浮点数和平方等运算，计算过程只有简单的整数乘法和加法。

2.2 双步圆推导

目前图形学的双步生成算法也逐渐被人们所关注。所谓双步法就是算法每一次循环产生两个象素，且双步生成算法与单点生成算法在每次循环中具有相同的计算量，所以双步生成算法仅使用了单点生成算法一半的循环量，这意味着双步圆的生成速度大约可以提高一半，因而算法在运算速度上比单点算法要快。

本文结合双步算法的思想以及改变像素级选取点的方法，设计出一个基于改进的bresenham画圆算法的双步画圆算法。

利用改变像素级算法中公式（5）的方法判定下一点是P1或P2的算法来进一步推导双步画圆的算法。

当选定P1后，下一个像素点为P3或P4点，这时用P3到圆的距离与P4到圆的距离之差与P1到圆的距离与P2到圆的距离之差做以下推导：

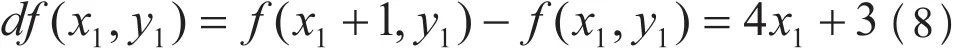
公式（8）中df (x1, y1)不是数学意义上的微分，而是用定义的距离之差的P1与P2的距离之差和P3与P4的距离之差的差值，即把这个差值推导成一种递推公式，等选下一点时可以根据P3与P4的距离之差向下推导，即当f (x, y)≤0时，df (x1, y1)表示P1，P2的距离之差与P3，P4的距离之差的差值，可以推导第二代与第三代的关系，以此类推。

1）若f (x0, y0)≤0时，根据公式（8）得出：

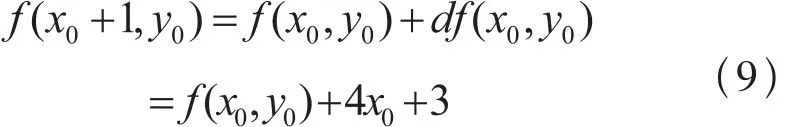
若f (x0+1, y0)≤0，取点P1(x0+1, y0),根据公式（9）得出：

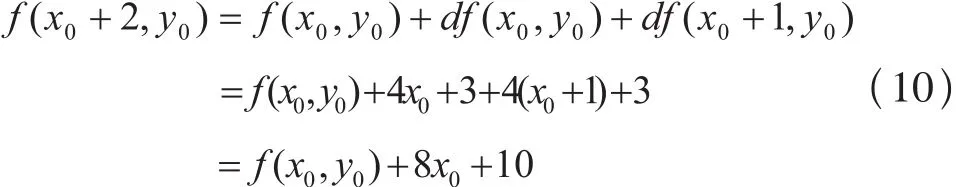
若f (x0+1, y0)＞0，取P2(x0+1, y0-1)，根据公式（9），（10）导出

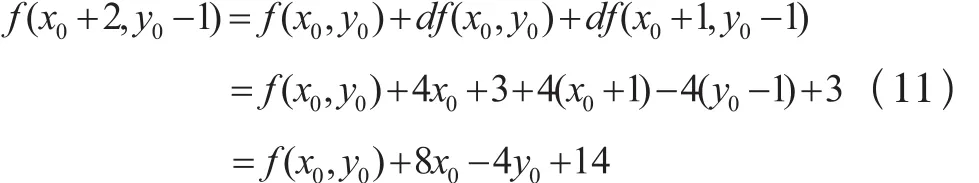
同f (x1, y1)≤0，导出当f (x1, y1)＞0时，

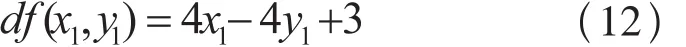
2）若f (x0, y0)＞0时，根据公式（12）导出：

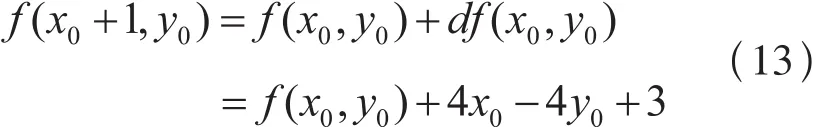
若f (x0+1, y0)≤0，取点P1(x0+1, y0)，根据公式（12），（13）导出：

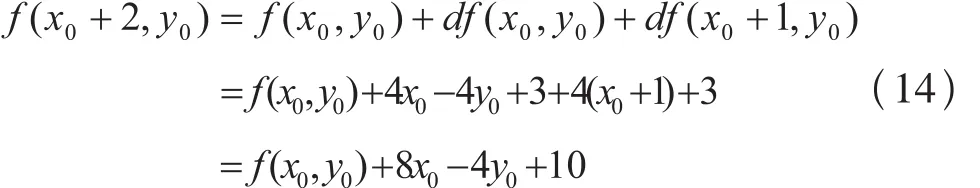
若f (x0+1, y0)＞0，取P2(x0+1, y0-1)，根据公式（12），（13）导出：

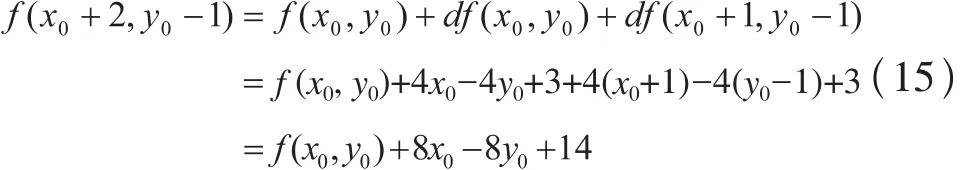
通过f (x0+2, y0)的符号就可以确定第二跳最接近圆弧的点。从而根据上一步中f (x0, y0)就可以确定下两个点的坐标，因此算法中每次循环可以确定两个点的坐标，实现双步画圆。

根据以上推导，生成基于改进的bresenham的双步画圆算法。

程序代码如下：

void DrawCircle(int x, int y, int r)

{ int m = 0,n = r;

int u,v;

long count = -2*r +1;

int i;

for (i=0; m＜n; i++)

{if (i＞0)

{ m += 1;

if(count＞0)

{count+=4*(m-n);

}

else

{count+=4*m+2;

}

if(count＞0)

{ n -= 1;

u=m;v=n;

m+=1;

count+=4*(m-n)-2;

if (count＞0)

{n-=1;

}

}

else

{ u=m;v=n;

m+=1;

count+=4*m+2;

if (count＞0)

{n-=1;

}

}

}

3 新算法与Bresenham算法的比较

3.1 新算法与Bresenham算法在速度比较

为了验证新算法的效率，本文对算法的执行速度进行了量化度量，并与Bresenham算法进行比较。对于算法速度通过分别用新算法与Bresenham算法测量画500个半径为200的圆所需要的时间来度量。在执行之前通过设置系统时钟函数clock()设定时钟，结束后通过此函数获取完成时间 。

运行结果： 用Bresenham算法画500圆需要的时间为3.131868秒；用新算法画500圆需要的时间为2.747253秒。结果表明，用新算法画圆的速度比Bresenham画圆算法速度要快。

3.2 新算法与Bresenham算法在精确度上的比较

对于算法精度比较，本文通过求画出圆上每一个点与实际圆的点的距离的平方差的平均值来进行新算法与Bresenham算法在精度上的比较。设目标圆弧点的坐标为法得出的对应的点的坐标为即通过以下公式来测量：

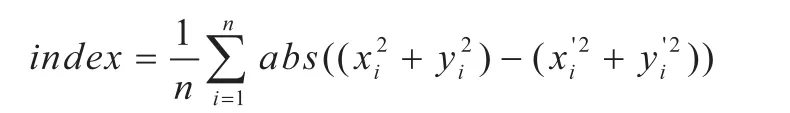
比较结果： Bresenham算法得出的方差为87.18881；而新算法得出的方差为68.433566。可以看出新的画圆算法比Bresenham画圆算法更接近真实，精确度更高。

4 结束语

通过以上的分析，改进的圆的算法无论在速度上还是精度上都要优于传统的Bresenham画圆算法。但是对于一些经典算法改进的余地已很有限，今后工作的重点应在对多步（多于双步）算法的开发上。多步算法结合圆的对称点方法将使圆的生成算法具有更快的速度。

[1] 孙家广, 杨长贵. 计算机图形学(新版)[M]. 北京: 清华大学出版社, 1995.

[2] 金廷赞. 计算机图形学[M]. 杭州: 浙江大学出版社,1988.

[3] 沈红.一个改进的象素级圆的单点生成算法[J].沈阳工业学院学报,2003, 22(2).

[4] 沈红. 一个圆的双步生成算法的提出[J]. 沈阳工业大学学报, 2002, 24(6).

[5] 王曙燕.C语言程序设计(第一版)[M].科学出版社,2008:23-58.