交联聚乙烯电力电缆电树枝生长的混沌特性分析

廖瑞金 周天春 刘 玲 周 湶 汪 可

（1. 重庆大学输配电装备及系统安全与新技术国家重点实验室 重庆 400044 2. 广州供电局 广州 510620）

1 引言

交联聚乙烯（Cross-Linked Polyethylene，XLPE）电力电缆由于其优越的绝缘性能在交流高压电力网中得到了广泛应用。运行经验表明[1]，XLPE电缆在电、热、机械和环境（水）等应力的长期作用下，会形成水树枝或局部弱区击穿，进而形成树枝状放电破坏通道，电树枝化产生以后很快就会发生完全或不完全的击穿[1,2]，因此电树枝化是制约XLPE电力电缆运行安全性和寿命的核心问题。

局部放电与电树枝生长过程密切相关，研究者们对电树枝产生局部放电的相位分布模式（Phase Resolved Partial Discharge，PRPD）特征[3-6]、单个波形特征[7,8]、趋势特征[9]和连续脉冲间的时间差特征[10]等进行了大量研究，期待找到合适的局部放电特征量，为电树枝的诊断服务，但是通常这些特征量缺乏相应物理机理的支撑。研究[11,12]认为电树枝的生长符合确定性混沌形成的条件，采用电树枝单位时间内局部放电次数（放电重复率）发展趋势作为观测对象，初步论证了电树枝生长的混沌特性；也有研究[13]将连续的局部放电脉冲间的时间、电压、和幅值差进行标准化后进行混沌分析，并认为它们的混沌特征可应用于XLPE电缆附件电树枝化的诊断。因此，有必要更深入地研究电树枝生长的混沌特性，以便更深入地了解电树枝生长的物理机理和找到能有效诊断电树枝的局部放电特征量。

本文采用实际的XLPE电缆作为试验样品，以针尖模拟电场应力的集中，在不同的电压和温度下得到了6个电树枝样品，引入了混沌理论分析电树枝生长的过程，并以电树枝局部放电单位时间内的最大放电量和总放电量作为分析对象，结合电树枝的生长的物理机理，提取并分析了电树枝生长的混沌特征。

2 混沌的基本原理与分析方法

2.1 相空间重构

时间序列被广泛应用于科学和工程技术领域，但由于时间序列是很多物理因子相互作用的综合反映，它蕴藏着参与运动的全部变量的痕迹，而把时间序列扩展到三维甚至更高维的相空间，能够充分显示时间序列蕴涵的信息，即时间序列的相空间重构。

在确定性的基础上，对系统动力学因素的分析，目前广泛采用的是延迟坐标状态空间重构法[14]，以便把时间序列中蕴藏的信息充分地显露出来。具体为：设{xn:n=1，2，…，N}是物理因子的时间序列，将其嵌入到 m维欧氏空间 Rm中，得到一个点（或向量）集J(m)，其元素记作

式中，τ 为时间延迟；m为嵌入维数；相点总数k=N-(m-1)τ，Xi为重构相空间相点，i=1,2,…,k。

2.2 时间序列的混沌检验

混沌的本质是系统内部的非线性作用机制，但并非任何非线性系统都会产生混沌，因此需要进行混沌检验。常用的混沌判别方法有 Lyapunov指数法、功率谱法、Poincare截面法和主分量分析法等方法。

Poincare映射能很好地刻画混沌的往复非周期特性，当Poincare截面上有且仅有一个不动点或少数几个离散点时，运动是周期的；当Poincare截面上是一封闭曲线，该运动是准周期的；如果Poincare截面上既不是有限点集也不是封闭曲线，则对应的运动就可能是混沌，更进一步，如果系统没有外部噪声扰动又有一定阻尼，Poincare映射的结果将是具有某种细致结构的点集。

2.3 时间序列的混沌特征提取

在初步确定时间序列具有确定性混沌特性的基础上，需要进一步地分析其特征，通常采用奇怪吸引子的统计特征，如 Lyapunov指数、分形维数、Kolmogorov熵来表征系统的宏观特征。

根据Takens定理[15]，需要找到一个合适的时间延迟τ和嵌入维数 m重构出系统在相空间的演化轨迹，即奇怪吸引子。在实际操作中最佳延迟时间的选取方法主要有以下几种：①互信息法；②其他信息论的方法，如冗余度法、信息熵等方法；③自相关法和复自相关法；④预报效果法等；其中自相关法和复自相关法的应用比较成熟，互信息应用比较广泛。求取最佳嵌入维数的方法主要有以下几种:①关联指数饱和法；②奇异值分解(SVD)；③伪最邻近点；④改进的伪最邻近点法；⑤预测效果法等。

3 XLPE电缆电树枝化试验及结果

3.1 试验样品

试验采用型号为 YJV22—3×95，8.7/15kV XLPE电缆作为试验样品，样品结构如图 1所示，电缆线芯直径11.5mm，内半导体屏蔽层厚0.5mm，XLPE绝缘层厚4.8mm，外半导体屏蔽层厚0.55mm，铜带紧贴外屏蔽层，以针尖模拟电场应力的集中,针尖到内半导体屏蔽层的距离为2.8mm。

3.2 试验线路

试验通过检测局部放电来监测电缆中的电树枝发展，因此采用数字化的局部放电检测方法，试验线路如图3所示，调压器、变压器、10kΩ保护电阻和1000pF的耦合电容组成一个50kV/50kVA无晕局部放电电源系统，传感器为铁氧体罗柯夫斯基线圈（带宽 50kHz～15MHz），局放信号经过 10～100倍的程控放大和 100kHz的高通滤波后，利用LeCroy Wavepro7100示波器（带宽1GHz，最高采样率20GS/s）进行观测和采集存储。

图1 XLPE样品结构Fig.1 Structure of the XLPE sample

图2 局部放电试验接线图Fig.2 Partial discharge testing circuit

加压结束的XLPE电缆样品，利用切片机将电缆切成1～3mm的薄片后，利用带摄像头的数码体式显微镜（最大放大倍数300倍）进行拍照观测。

3.3 试验结果

基于针-板电极系统的研究结果表明[8-10]：电树枝生长过程很复杂，受到多因素的影响，如针电极结构（曲率半径）、材料、电压、温度、频率以及试样的处理等等。对于实际运行中的XLPE电力电缆，电压频率是固定的工频，电场应力集中的形式是未知的，但是额定运行的温度达90℃，所以对于实际XLPE电力电缆电树枝化最主要的坏境影响因素为电压和温度。

因此制作了6组电缆样品进行试验，样品a、b、c、d在常温下分别以 1kV/s的升压速度升压至12kV、15kV、18kV和21kV后稳定，样品e、f分别在50和70℃下以1kV/s的升压速度升压15kV后稳定，观测并记录局部放电数据，为了数据对照的方便，在最大放电量达到1500pC左右时结束加压，切片并观测电树枝。

试验结果见表1和图3所示，其中D1为横截面切片观测的树枝宽度，D2为纵截面切片观测的树枝宽度。

表1 不同电树枝试验结果Tab.1 Results of different electrical trees

图3 不同电压下的电树枝照片Fig.3 Photos of electrical trees under different voltages

4 电树枝生长的局部放电混沌特性分析

4.1 混沌时间序列选择

混沌描述的是一个过程，而不是一种状态，为研究电树枝生长的混沌特性，必须首先确定一种可测变量，它的数值将反应出能控制生长随机涨落的局部参数。可通过局部放电的数值来测量电树枝的生长随机涨落，主要包括放电次数和放电量，Dissado[12]对单位时间内的放电次数的时间序列进行了混沌研究。然而，放电次数的统计受测量系统灵敏度的影响较大，即较小的局部放电脉冲可能会被忽略掉，因此本文选取局部放电放电量的时间序列作为混沌研究的时间序列。

和放电次数时间序列一样，首先需要得到等时间距离观测的放电量时间序列，即需要选择一个合适的时间距离。结合已有的研究经验和混沌分析样本量的需求，每0.3s统计一次数据，a、b、c、d、e和f样品 6组电树枝的时间序列如图4和图5所示，总样本点数 N 分别为 2 400、2 000、2 000、5 000、2 000和2 000。

图4 最大放电量时间序列Fig.4 The time series of maximal PD magnitude of electrical trees propagation

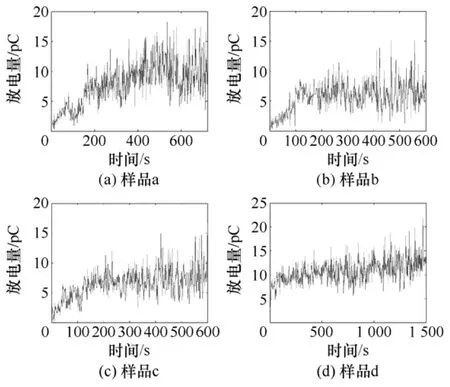
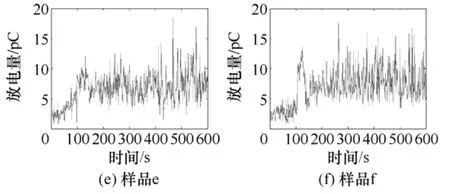
图5 总放电量时间序列Fig.5 The time series of total PD magnitude of electrical trees propagation

为了消除伪数据与干扰的影响，在混沌分析之前对序列进行标准化处理，已知时间序列{yk：k=1，…，N}是等时间距离观测得到的放电量时间序列，对该序列进行标准化处理，见式（2）。

式中，ymin=min{yj，j=1，2，…，N}，ymax=max(yj，j=1，2，…，N)

4.2 混沌时间序列初步检验

采用Poincare截面法进行初步检验，得到15kV常温下的电树枝样品b的最大放电量和总放电量的时间序列的Poincare截面如图6所示。图6a中，x(n)和 x(n+τ)表示相空间重构后的最大放电量和延迟时间τ 得到的最大放大量；图 6b中，x(n)和 x(n+τ)表示相空间重构后最大放电量和延迟时间τ得到的总放电量。

图6 PD时间序列的Poincare截面Fig.6 Poincare sections of the time series of PD

结果显示所有序列的Poincare截面上均是一片具有分形结构的密集点，因此初步分析的结果表明最大放电量qmax和总放电量qn的时间序列具有确定性混沌特征。

4.3 混沌特征提取

采用互信息法[14]计算得到τ =3时可较好地消除人为相关，然后采用Cao氏方法计算嵌入维数m=10。

Laypunovr指数采用适合于小数据量的方法，即小数据量法[17]进行计算。具体步骤如下：

（1）根据以上延迟时间τ和嵌入维数m的计算结果，进行相空间重构

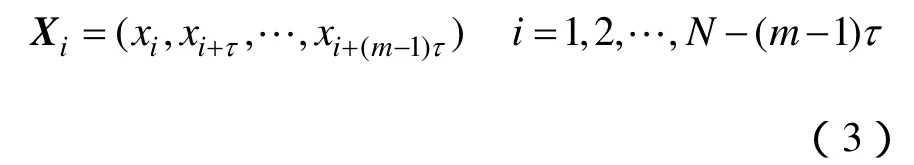
（2）从X1开始计算每个相点Xi的最近邻点Xj，并限制短暂分离，即

在此之前，收敛了昂扬姿态的王树林在看电视。他在等辛娜的出浴。眼睃着屏幕，耳朵一直在浴室的响动中。他的手里拿着手机若有所思。很快浴室的水声停止了，他收起手机，快步来到浴室门外。略一迟疑，伸手拧开了浴室的门，一股香波味儿扑鼻弥香，淡薄的水汽里辛娜正抬腿擦拭，晶莹的水珠在光洁丰腴的后腰闪耀着诱人的光点。不假思索，王树林躬身抱起了出水芙蓉，惊得辛娜哎呀一声一下子揽住了王树林的脖子。两条修长白皙的大腿不停在半空踢踏，别有一番情调。

（3）对相空间中的每一对最近邻点计算k个离散时间步后的距离di(k)，即

式中，n=N-(m-1)τ为重构相空间相点总数。

（4）求出所有di(k)不为零的对数ln(di(k))，并对每一个k，计算基于i的平均值y(k)，即

式中，M是针对某个k值的非零di(k)的数目。

（5）运用最小二乘法计算曲线的斜率，该斜率值即为最大Lyapunov指数λ1。

运用上述方法求得 6组样品的最大放电量和总数电量时间序列的最大Lyapunov指数λ1结果见表 2。

表2 最大Lyapunov指数Tab.2 The maximal Lyapunov exponent

6组样品 qmax和 qn时间序列的最大 Lyapunov指数λ1均为正数，这也证实了电树枝局部放电放电量的时间序列具有确定性混沌特性。

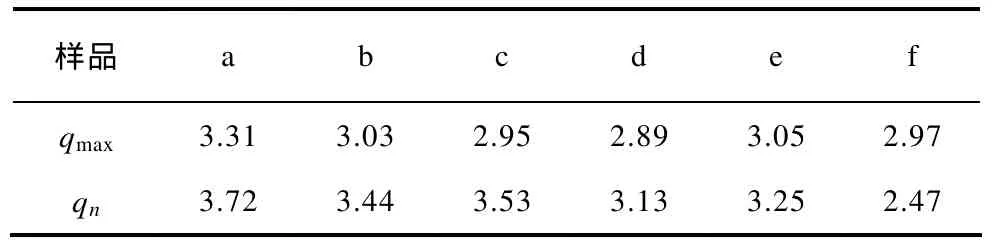
表3 关联维数Tab.3 Correlation dimension

4.4 讨论

电树枝形态可将电树枝分为枝状、丛林状、枝丛混合状，纯枝状电树枝一般迅速连续生长，丛林状电树枝生长过程一般存在较长时间的停滞期，生长速度较慢，因此通常枝状电树枝的危害要大于丛状电树枝[2]。分形维是表征电树枝形状特征的重要参数，枝状电树枝的分形维数小，丛林状电树枝分形维数大。通过改变覆盖图形的正方形的边长r来分别求取不同边长r下覆盖图形的方格数，可计算电树枝的二维分形维数D，具体计算公式如下[17]：

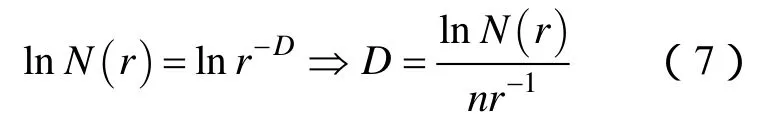
奇怪吸引子的最大 Lyapunov指数和关联分形维数定量表征了系统的混沌度，最大 Lyapunov指数表征系统的不稳定性，关联维数表征系统变化的复杂性。试验得到的电树枝分形维与最大Lyapunov指数、关联分形维数的关联分别如图7和图8所示。从图上可以看到最大 Lyapunov指数、关联分形维数均有随着树枝分形维数的增大而减小的趋势，但是很明显总放电量时间序列得到的混沌特征的分散性比较大，分析认为越大的局部放电在树枝管道中扩展的距离越远，也更容易到达树枝尖端[18]，因此较大的局部放电脉冲是诱发电树枝生长的重要因素，且环境噪声及检测系统的灵敏度对较大局部放电的测量结果影响比总放电量要小，即抗噪声能力要强，所以最大放电量发展的时间序列比总放电量的时间序列更好地表征了电树枝局部电场的涨落。

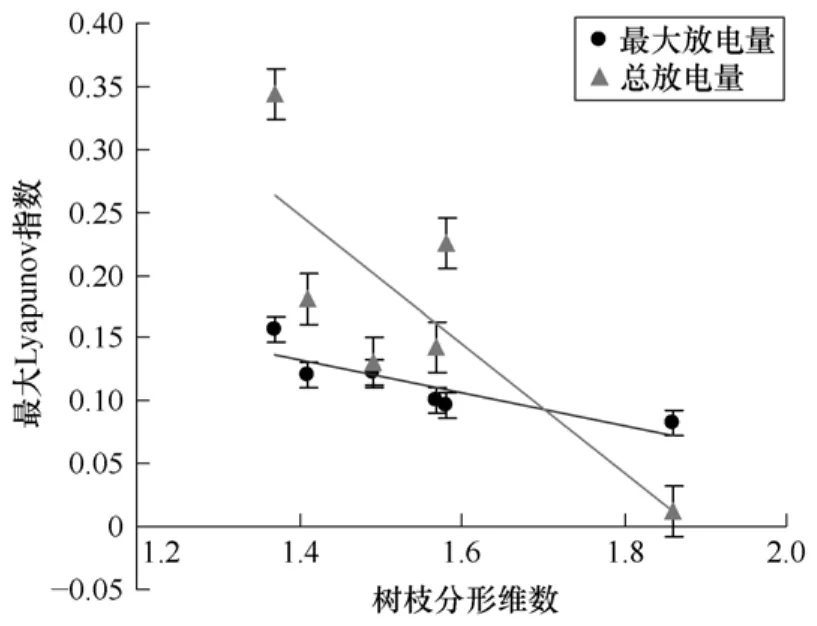
图7 电树枝分形维与最大Lyapunov指数关系Fig.7 Relationship of fractal correlation dimension and the maximal Lyapunov exponent

图8 电树枝分形维数与关联分形维数关系Fig.8 Relationship of the electrical tree fractal dimensions and correlation dimensions

电树枝分形维数的增大，最大 Lyapunov指数和关联维数均减小，这说明丛状电树枝的生长过程比较平稳，随机性较小。分析认为丛状电树枝具有更密的树枝通道，且通道电导更高[17]，空间电荷的转移会比较容易，这促使电树枝通道附近的局部电场涨落比较均匀，不容易积累起较多电荷，形成较大的局部放电，而通常较小的局部放电不容易传播到树枝末端[18]，从而发展比较平稳，这也是通常丛状电树枝生长速度比枝状电树枝发展慢的重要原因，电树枝的混沌特征与其生长机理可以相互印证。

同时，升压速度对电树枝生长的影响也进一步的证实了枝状电树枝对初始条件的敏感性比丛状电树枝要强，即最大Lyapunov指数要大。图9为12kV和21kV，0.1kV/s和1kV/s升压速度下电树枝样品的形态（横截面）的对照，在 12kV下由于升压速度的改变，电树枝分形维数由 1.22变成 1.37，而21kV下变化较小，由1.83变成1.86，即12kV下枝状电树枝对初始条件的敏感性要强于 21kV下的丛状电树枝。

图9 0.1kV/s和1kV/s升压速度的电树枝照片Fig.9 Photos of the electrical trees under different boost speed stressing

综上所述，局部放电的混沌度与电树枝的形态相关，奇怪吸引子的最大 Lyapunov指数和关联分形维数随着树枝分形维数的增加而减小。

5 结论

（1）XLPE电力电缆电树枝化试验结果显示电树枝生长存在确定性混沌机理的可能，Poincare截面、最大 Lyapunov指数和关联分形维数的结果均显示电树枝局部放电时间序列具有确定性混沌特征，证实了XLPE电缆电树枝的生长过程具有确定性混沌特性。

（2）最大放电量和总放电量时间序列的最大Lyapunov指数和关联分形维数值均表现出随树枝分形维数的增大而减小的趋势，与枝状和丛状电树枝对升压速度影响敏感性的结果相符。

（3）局部放电时间序列的混沌特征可以作为判断电树枝形态特征的参考量，且最大放电量时间序列的表征效果要优于总放电量的时间序列。

[1](日)速水敏幸. 电力设备的绝缘诊断[M]. 刘晓萱,译. 北京: 科学出版社, 2003.

[2]李盛涛, 郑晓泉. 聚合物电树枝化[M]. 北京: 机械工业出版社, 2006.

[3]J Y Koo, J S Lee, J T Kim. Study on the correlation between the PD pattern and the aspect of electrical trees propagation in the XLPE insulation of the underground power transmission cable[C]. Proceedings of the IEEE 6th International Conference on Properties and Applications of Dielectric Materials,2000,1: 161-164.

[4]S H Park, K J Lim, S H Kang. Characteristic analysis of electrical tree initiation using PD distribution and statistical parameters in variable defected models in solid insulator[C]. Proceedings of the IEEE 8th International Conference on Properties and Applications of Dielectric Materials, 2006, 3: 579-582.

[5]G L Wu , X W Jiang. Experimental study on tree growth in XLPE using 3D PD patterns[C].Proceedings of the IEEE International Conference on Properties and Applications of Dielectric Materials,2000, 1: 558-561.

[6]F Guastavino, B Cerutti. Tree growth monitoring by means of digital partial discharge measurements[J].IEEE Dielectrics and Electrical Insulation, 2003,10(1): 65-72 .

[7]T Kalicki, J M Braun. Pulse-shape characteristics of partial discharge within electrical trees in polymeric materials[C]. IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), 1995,11: 380-383.

[8]J Densley, T Kalicki, Z Nadolny. Characteristics of PD pulses in electrical trees and interfaces in extruded cables[J]. IEEE Dielectrics and Electrical Insulation,2001, 8(1): 48-57.

[9]G C Montanari. Aging and life models for insulation systems based on PD detection[J]. IEEE Dielectrics and Electrical Insulation, 1995, 2(4): 667-675.

[10]A Cavallini, G C Montanari, F Puletti. A fuzzy logic algorithm to detect electrical trees in polymeric insulation systems[J]. IEEE Dielectrics and Electrical Insulation, 2005, 12(6): 1134-1144.

[11]L A Dissado. Deterministic chaos in breakdown does it occur and what can it tell us?[J]. IEEE Dielectrics and Electrical Insulation, 2002, 9(5): 752-762.

[12]L A Dissado. Understanding electrical trees in solids:from experiment to theory[J]. IEEE Dielectrics and Electrical Insulation, 2002, 9(4): 483-497.

[13]J Y Koo, J S Lee, J T Kim, et al. Comparison of diagnostic method for pattern analysis due to artificial defects introduced at the interface in XLPE cable joint using laboratory model[C]. Proceedings of the IEEE Power Engineering Society Transmission and Distribution Conference, 2002, 2: 1426-1431.

[14]吕金虎，陆君安，陈士华. 混沌时间序列分析及其应用[M]. 武汉: 武汉大学出版社, 2002.

[15]F Takens. Determing strange attrange attractors in turbulerce[J]. Lecture Notes in Math, 1981, 898:366-381.

[16]M T Rosenstein, J J Collins, C J De Luca. A practical method for calculating largest Lyapunov exponents from small data sets[J]. Physica D, 1993, 65(1-2):117-134.

[17]张济忠. 分形[M]. 北京: 清华大学出版社, 1995.

[18]H Kaneiwa, Y Suzuoki, T Mizutani. Characteristics of PD pulse sequence and single-pulse light emission in artificially-simulated tree channel[C]. IEEE Conference on Electrical Insulation and Dielectric Phenomena(CEIDP), 1999, 2: 601-604.