基于小波变换的导线绝缘故障定位方法
张俊民 周小猛 魏 娟 曹大树 姚红宇
(1. 北京航空航天大学自动化科学与电气工程学院 北京 100191 2. 中国民用航空总局航空安全技术中心 北京 100028)
1 引言
飞机导线系统是飞机的重要组成部分,为飞机各部件提供动力电源、控制信号和数据信息。随着飞机机龄的增长,导线长期在化学、冷热、电、振动、摩擦、外力、污染和辐射等复杂环境下工作以及由于维护不当等原因,会产生绝缘磨损、老化、腐蚀和变形等故障(又称软故障),并最终造成导线的断路或短路(又称硬故障)。目前,已经有许多种检测导线故障的方法,如目测法、电阻法、闪测法和声测法等。但这些方法或者所用电压太高、或者只能有效定位硬故障,均不能用于连接有大量精密仪器且对可靠性要求极高的飞机导线上。时域反射法[1](TDR)是一种无损检测方法,它向导线注入上升时间较短的低压脉冲或矩形波,通过分析接收到反射信号中包含的导线特征阻抗变化信息,确定导线是否存在绝缘故障;通过测算入射波形和故障处反射波形起始点的时间差,确定故障位置。为此,国内外已经开始了将 TDR用于飞机导线故障检测的初步研究[2-4]。
在TDR中,反射波包含的大量噪声,有可能湮没较小的故障信息,同时影响起始点的测定。用传统的 Fourier去噪方法不能同时满足滤掉噪声和保留信号突变部分的要求。小波方法具有自适应的时频局部化功能[5-8],它根据高频信号和噪声在不同变换尺度下的相异表现,有效地消除噪声;利用突变部分在连续小波变换下的模极大值,精确定位反射波形的转折点。
本文基于 TDR建立航空导线绝缘故障的数学模型,并以此构建检测信号在有损耗故障导线中传播的仿真模型;搭建TDR试验平台,检测小尺寸的绝缘故障;对反射波形运用小波方法去除噪声并确定故障处尖峰的起始点,精确地测定故障位置,为TDR的实际应用提供一定的实验基础。
2 航空导线绝缘故障的数学模型
飞机导线的结构形式为有屏蔽的单芯电缆和多根电缆以及无屏蔽的单芯电缆和多根电缆的导线束,故导线绝缘故障的表现形式会多样化。为了方便研究导线绝缘变化后,其特征阻抗的变化对入射电磁波传播过程的影响,以图1所示导线绝缘层对称减小时的故障情况为代表进行TDR的分析。其他的绝缘变化情况下,如非对称的绝缘层减小,特征阻抗的变化对电磁波传播过程的影响是相似的。

图1 导线绝缘损坏模型Fig.1 Frayed wire insulation model
TDR的理论依据是传输线理论。假定图1中导线的电气参数在完整处和故障处是各自不变的,只在交界点发生突变,则可以把完整处和故障处导线看作两种参数不同的传输线,是由沿线均匀分布的等效电阻、电导、电感和电容构成的电路。若始端入射电压为u0,则在完整段或故障段,任意时刻任意位置的电压、电流方程为[9]

式中,R为导线单位长度的电阻,Ω/m;L为导线单位长度的电感,H/m;G为导线单位长度的电导,S/m;C为导线单位长度的电容,F/m;u、i分别为距离始端x处的电压、电流。
若导线始端的电压是角频率为ω 的正弦时间函数,则沿线的电压、电流是同一频率的正弦时间函数,用相量法求解式(1)得到任意位置的电压、电流为
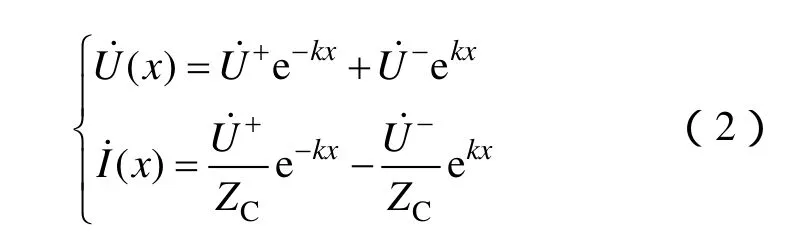
式中,k,ZC分别为导线的传播常数和特征阻抗
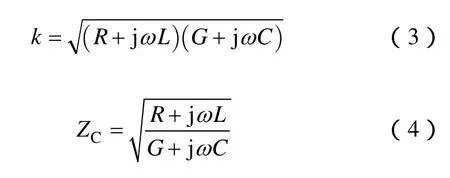
式(2)所表示的暂态解可分为入射波和反射波两个分量,入射波在阻抗不匹配处发生反射和透射。如果导线中某处出现故障,则故障处几何参数的变化引起特征阻抗的改变,从而在该处发生波的反射和透射。对于图1所示的导线绝缘故障,输入信号沿导线传播,经过延时衰减到达故障界面1时,由于阻抗不匹配,会产生一个继续向前传播的透射脉冲 U˙12和一个向始端传播的反射脉冲 U˙11。设导线的故障处距离始端的长度为l1,则由式(2)可得在故障处的反射波和透射波分别为

式中,ρ1为沿入射信号方向界面1的反射系数

τ1为透射系数,ρ1≠1时,τ1=ρ1+1;ρ1=1时,τ1=0;k1为完好处导线的传播常数;ZC和ZL分别为完好处和故障处导线的特征阻抗。
考虑多次反射后,对于图1的单个绝缘故障,导线中信号的传播过程可用如图2所示的数学模型来描述。

图2 波在故障导线中传播的数学模型Fig.2 Mathematical model of wave transmitting process in fault wire
图2中,ρ1~ρ3分别为界面 1、界面 2及终端从入射信号方向看过去的反射系数;τ1和τ2分别为界面1和界面2的透射系数;k1与k2分别为完好处导线与有绝缘故障处导线的传播常数;l1~l3为导线各部分的长度;U0为入射电压,U1~U5分别为导线特征阻抗变化处入射波、反射波的电压,其值随反射次数的不同而不同。另外,该模型可以推广至多个故障时的情况,只需要依据式(2)建立起完好导线与故障导线的联系即可。
3 有损耗故障导线的TDR仿真
根据图2的数学模型,便可以在Matlab中建立相应的仿真模型。文献[3]在仿真时忽略了导线的电阻和电导,这样反射系数为一个-1~1的实数,给计算带来了很大的方便。但为了使仿真模型能更精确地反映实际导线,下面考虑在模型中加入电阻和电导的情形。
图1所示导线的电阻和电导值可以通过相关公式求得[10],它们均和入射信号频率有关。由式(3)、式(4)和式(7)可知,传播常数、特征阻抗以及反射系数也都是频率的函数。为此,在仿真时先对入射信号进行高次傅里叶分解,确定其频谱,将得到的各次谐波替代入射信号送入导线;再计算对应频率下导线的二次参数及故障处的反射系数,并根据图2算出反射信号;最后将不同频率下的反射信号叠加,便得出对应于入射信号的反射信号。
在计算各个频率下的反射信号时,可以将图 2的数学模型转化为如图3所示的信号流图模型。其中,X为入射信号,Y为反射信号;ρ1~ρ3、τ1和τ2的含义和图 2中的相同;G1~G3分别为信号在导线l1~l3段传播的增益,可由各段的传播常数k表示为
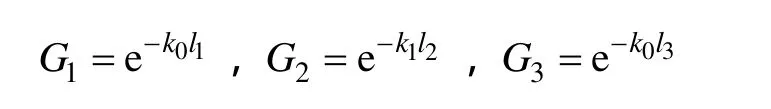

图3 波在故障导线中传播的信号流图Fig.3 Signal flow graph of wave transmitting process in fault wire
图3中,点划线框包围部分为导线末端和一段绝缘故障的信号流图,3和 4之间代表导线末端。若需要构造两段故障的信号流图,只须先将图3中的点划线框中部分复制,再去掉原图中3和4间的方框,并把断开处3和4分别与复制虚线框的端口1和2相连。多个故障时的信号流图依此类推。
将图3所示的信号流图化简,算出各次谐波从故障导线的发送端到接收端的总增益,再将由此计算出的Y叠加,便得到最终结果。
由于矩形波的故障检测效果优于脉冲波,且波形的上升时间与所能发现故障的最小长度有很大的关系[3]。故在仿真时,使用上升时间 tr分别为10ns和5ns、幅值均为5V的方波作为入射信号,检测两种图1所示的故障。终端开路,完好段导线长度l1和l3都为10m,聚四氟乙烯绝缘层厚0.6mm;故障段长度 l2分别为 0.1m 和 0.05m,绝缘层厚0.2mm;铜芯直径2mm。一个周期的接收端波形如图4所示。

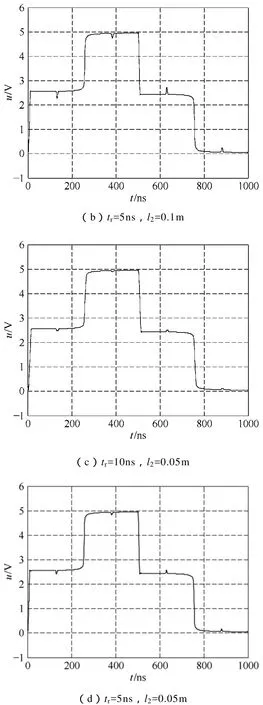
图4 不同条件下故障导线的TDR仿真结果Fig.4 TDR simulated results of fault wire in different conditions
从图4中可以看出,尽管入射波的上升时间很短,但传播时高次谐波的大量衰减,使得TDR波形的转折平缓了许多,较难准确测定其起始点。相同的故障长度下,入射波的上升时间越短,接收端波形上对应故障处的峰值越高,特征越明显,但同时尖峰变得更窄,不易被采样到;相同的入射波的上升时间下,故障越短,对应的幅值越低,短至一定程度,尖峰会因太小而湮没在噪声之下,难以被发现。
实际检测时,被检导线通常较长,而故障一般很短,反射信号受噪声干扰严重,影响着对故障的诊断和准确定位。为此,需要先消除其噪声。另外,反射波形的转折比较平滑,传统的确定反射波起始点的目视法误差较大,因此需要运用小波方法精确测定起始点。
4 模拟故障导线的TDR试验
利用信号发生器和示波器、采样单元以及导线建立TDR试验平台,如图5所示。自制的信号发生器产生周期 240Hz、上升时间约 5ns的矩形波;采样和示波单元采用数字示波器Tektronix TDS5032B;导线采用双绞线和同轴电缆等不同特征阻抗的导线组合连接,与仿真中将导线绝缘层变薄的目的类似,都是为了降低导线某一处的特征阻抗。

图5 TDR试验平台构成原理图Fig.5 Principle diagram of TDR test setup
在试验中,由于输入信号的周期远大于其在导线中的传播时间,所以对于被试导线,输入信号的每个周期都相当于输入一个阶跃信号,得到各个周期内的波形均相同,因此只需分析一个周期内的信号波在导线中的传播情况即可。
在两根长度分别为4.28m和3.7m的双绞线(特征阻抗100Ω)之间串联一根0.1m长的同轴电缆(特征阻抗50Ω)。向导线的一端注入TDR检测信号,测得的发射端电压波形如图6所示。

图6 特征阻抗变化的TDR波形Fig.6 TDR waveform of characteristic impedance change
图6为反射波形的上升沿部分,前端有较小的振荡,这是由信号发生器和导线的阻抗不匹配引起的。在阶梯的中部,可以看到小幅度的负尖峰(圆圈处),说明导线在该处的特征阻抗变小,对应着0.1m的同轴电缆。与仿真结果相比,尖峰持续时间更长,变化更平缓,原因应该在于噪声的干扰和连接处反射透射的损耗。其后波形的再次上升是由导线末端的全反射造成的。
为了定位故障,观测到图6中入射波、故障处尖峰和末端反射波的起始时刻分别为20ns、62ns和97ns,再利用导线的总长 l=4.28+3.7+0.1=8.08 m,算出波速度

由此得到故障起始点到发送端的距离
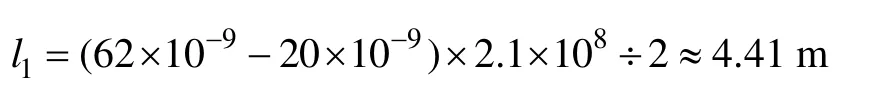
与实际值4.28m相差0.13m。噪声的干扰、起始点波形的平缓变化以及目测的不准确,是造成比较大的定位误差的主要原因。
故障缩短后,其在TDR波形上的特征将会难以直接分辨。例如,将上述串联的同轴电缆换至5cm长,测得的TDR波形如图7所示,可以观察到波形的细微负尖峰(圆圈处),代表连接处的阻抗减小。尖峰的幅值与噪声水平相当,不易被发现。和测定图6所示故障位置的方法一样,算出故障点距离发送端 4.43m,超过实际值 0.15m,定位仍然不够精确。

图7 故障缩短后的TDR波形Fig.7 TDR waveform of shortened fault
5 TDR波形的小波去噪和故障点定位
实际中,导线的绝缘故障部分通常都很短,至多几厘米。从上节的TDR试验波形上来看,较短故障的特征并不明显,容易被噪声掩盖;同时,目测确定尖峰起始点的方法,容易造成比较大的定位误差。为此,本文先利用小波方法去除试验波形的噪声,再通过不同尺度下的连续小波变换定位故障。
小波去噪的方法有许多种,如相关法、模极大值法和阈值法等。由于TDR波形的噪声幅值较低,故选用不需要估计噪声方差且不会产生伪极值点的阈值去噪法。对于图7的小范围故障波形,经试验,利用db4小波对其作5层分解,选择启发式软阈值,去噪效果较好,结果如图8所示。虽然起始处的振荡仍很明显,但去除了原始波形中的大部分噪声,同时保留了起始点和故障点信息,易于分辨故障特征。

图8 去噪后的TDR波形Fig.8 De-noised TDR waveform
由于 TDR波形的转折点与对应小波变换的模极大值密切相关。因此,对去噪后的波形进行连续小波变换,寻找模极大值点,可以确定入射波、故障处和反射波的起始点。
对于图8去噪后的波形,故障处变化较为平缓,故选择对称性好且阶数较高的 sym6小波,进行尺度为20的连续小波变换,结果如图9所示。
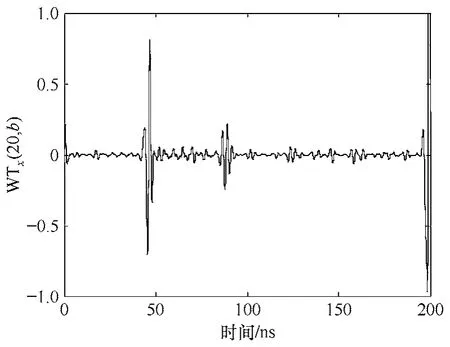
图9 去噪后经过连续小波变换的波形Fig.9 Continuous wavelet transform of de-noised waveform
由图8和图9分析可知,小波变换的模极大值在3个地方较大,分别对应着入射波、故障处的起始点以及波形的末端。末端的模极大值最高,是由对末端以外的数据直接取零产生的突变造成的。反射波的起始点在约120ns处,经过末端的反射以及导线的损耗,波形变得平缓,因而其模极大值较小。
图8中入射波和反射波起始处波形都是凹的,故取模极大值处的第一个极小值作为其起始时刻;相应地,故障处的波形是凸的,取第一个极大值。由此测得所需的波形起始时刻分别为 45.62ns、86.43ns和122.4ns,与导线的总长度8.03m一起,算出故障距离始端 4.27m,十分接近于实际值,与上节的测量结果相比精度提高了很多。
为了进一步验证该方法的有效性,选取不同长度和规格的导线进行TDR测试及故障定位,结果见下表所示。

表 小波方法定位不同故障的精度Tab. Precision of locating different faults in wavelet
可以看到,对于不同的导线,小波方法的绝缘故障定位精度均比较高,但故障处到始端的距离增加后,定位精度有所下降,这可能是由于信号在未屏蔽导线中传播时,波速度的不稳定造成的。
6 结论
本文基于 TDR建立了航空导线绝缘故障的数学模型,并在考虑导线电阻和电导的情况下,使用方波作为检测信号,进行了绝缘故障导线的TDR仿真。由于传播时高次谐波的衰减,使得接收波形的转折变得平滑,起始点不易被精确测定;为了探测小尺寸的绝缘故障,需要有陡峭上升沿的入射波和高速度的采样仪器,并对接收到的波形进行消噪处理。
搭建了TDR试验平台检测导线的绝缘故障,实际波形与仿真结果相吻合,但传统的目测确定起始点的方法有较大的误差。为此,对接收到的波形用小波方法去除噪声并确定转折点。结果表明,该方法有助于识别细微的绝缘故障,并提高故障定位精度。
[1]Auzanneau F, Olivas M, Ravot N. A simple and accurate model for wire diagnosis using reflectometry[AC]. Proceedings of Progress in Electromagnetics Research Symposium, Prague,2007.
[2]张俊民, 谢华博, 魏娟, 等. 飞机电缆绝缘缺陷与故障的检测技术及分析[J]. 航空维修与工程, 2008,10(1): 26-29.Zhang Junmin, Xie Huabo, Wei Juan, et al. Aircraft cable fault detection technology and its analysis[J].Aviation Maintenance & Engineering, 2008, 10(1):26-29.
[3]张俊民, 魏娟, 谢华博, 等. 基于时域反射法的航空导线绝缘故障检测与分析[J]. 航空学报, 2009,30(4): 706-712.Zhang Junmin, Wei Juan, Xie Huabo, et al. Detection and analysis of aerospace wire insulation faults based on TDR[J]. Acta Aeronouticaet Astronautica Sinica,2009, 30(4): 706-712.
[4]Griffiths L, Parakh R, Furse C, et al. The invisible fray: a critical analysis of the use of reflectometry for fray location[J]. IEEE Sensors Journal, 2006, 6(3):697-706.
[5]胡光书. 现代信号处理教程[M]. 北京: 清华大学出版社, 2004.
[6]徐长发, 李国宽. 实用小波方法[M]. 武汉: 华中科技大学出版社, 2004.
[7]周伟. MATLAB小波分析高级技术[M]. 西安: 西安电子科技大学出版社, 2006.
[8]张炳达, 瞿敏, 陈伟乐. 软阈值消噪法在电缆故障测距中的应用[J]. 仪器仪表学报, 2003, 24(4):506-507.Zhang Bingda, Qu Min, Chen Weile. The application of soft-threshold de-noising in cable fault location[J].Chinese Journal of Scientific Instrument, 2003, 24(4):506-507.
[9]邱关源. 电路[M]. 4版. 北京: 高等教育出版社,2001.
[10]P. 格里维. 高频传输线的物理基础[M]. 黄鹤松,译. 上海: 上海科学技术出版社, 1984.

