缓解交通拥挤的多目标优化模型和算法研究
吴中,何群
(河海大学 土木与交通学院,江苏 南京 210098)*
0 引言
随着我国社会经济和城市化水平的发展与提高,交通拥挤成为困扰许多大城市的难题,单纯的增加交通供给已被证明不能解决拥挤问题,征收“拥挤费”作为交通需求管理的一种形式,成为大城市缓解拥堵的备选方案.交通拥挤收费的理论最初由Pigou于上个世纪20年代提出,之后Waters和 Vickery继承并发展发展了 Beckman[1](1965)的理论,提出出行者支付费用使用拥挤道路,可以平衡边际社会成本与边际个人成本之间的差值,达到系统最优的目的.征收“拥挤费”在国外已经成功施行多年,新加坡的成果最为显著[2].从1975年开始的人工收费系统(ALS)发展到现在的电子收费系统(ERP),收费使常年日交通量减少15%,上午7:30~9:30高峰小时交通量减少16%,多次进入限制区的交通量减少到34%.国外经验表明,拥挤收费是缓解交通拥挤行之有效的管理手段.
国内对拥挤收费的研究起步较晚,李志纯等[3](2001)利用双层规划模型与步长加速法和罚函数法组合的启发式算法对弹性需求下的道路收费问题进行了研究,给出了不同路段的收费费率,以求达到网络交通流的平衡,但其方法复杂、费率变化,难以推广应用.郭瑞军、王晚香等[4](2008)运用定量和定性方法探讨了交通拥挤中社会和个体成本的组成,以及两者之间的关系,但未给出应用于实际的计算模型.张琳琪、宋瑞等[5](2008)基于UE均衡原则,分析交通收费条件下的用户和系统的关系,从而确定拥挤收费费率,但其方法主要考虑交通平衡,未计社会总成本的损失.本文在综合考虑流量与成本的关系基础上,构建了合理阻抗函数,以个体成本总量和社会总成本最小化为目标建立多目标模型,并给出相应的算法,分析不同拥挤费对交通配流的影响,以达到多路径选择下个体与社会总成本最优的目的.
1 建立模型
1.1 目标函数的确定
出行者路径选择不当会造成自身出行费用的增加,这种自身承担的损失成本叫做内部成本.不当路径选择还会造成其他道路使用者、交通资源与社会环境乃至生活中无直接联系的第三方的损失,由于自身车辆的加入而使道路更加拥挤,导致其他各方增加的成本叫做外部成本.
个体成本是指个体出行者在出行过程中的行驶时间、车辆折旧、油耗费、拥挤等内部成本.社会总成本包括所有个人成本,交通设施设备的消耗成本,还包括大气污染、道路公司流量损失等外部成本.
个体成本小说明出行者选择了利于自己的出行路径;社会总成本小说明交通管理组织有效.仅凭个人成本总量最优或是社会总成本最优还不能很好地确定拥挤费取值,以个人成本总量和社会总成本最小为目标构建规划方程,通过协调控制两者的大小,可以兼顾各方利益,合理地确定交通拥挤费率.
1.2 阻抗函数的构建
单个出行者往往只考虑内部成本,选择路线阻抗函数较小的路线,忽视给他方带来的不便与损失,致使某些道路资源在特定时段出现使用紧张或过度闲置的现象,造成社会外部成本增加.道路阻抗函数和行驶时间、距离、通过费用等内部成本有关.其中影响阻抗大小的主要因素是行程时间和通过费用,由于交通能源消耗、舒适性、安全性等因素都与行程时间和通过费用有关,本文只考虑行程时间、通过费用这两个主要因素,形成包括行程时间费用和通过费用的广义费用,即
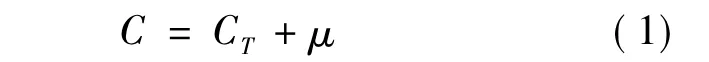
式中,C为广义费用;CT为行程时间费用;μ为道路通过费用,交通“拥挤费”也应计入在内.
在式(1)中,CTi是车流量为xi时车辆通过路段i所需的时间费用.显然,随着车流量的增加,时间费用不断增加,当车流密度达到临界时,车流量不增反降,但时间费用仍然呈现增加趋势.具体如图1所示.μ的取值范围要考虑当地的经济、文化和时间价值以及出行者接受水平.

图1 交通量与行程时间费用的关系图
设路段i的交通容量为pi,零流量情况下车辆通过的行程时间费用为Ai,参考美国BPR公式,利用时间价值系数γ同质化行程时间函数转换成费用有:

式中,xi为路段i的当量标准车流量;pi为路段i的基本通过能力.行程时间费用CTi右端第一项为正常行驶行程时间费用,第二项ε是由于行程时间易受天气、交通事故影响而考虑的随机应变量,服从正态分布.
1.3 多目标非线性规划模型
出行者选择主观上的最优路径,不支付因为自身给系统带来的额外延误,受益大于支出,为了缓解管理方与出行者之间的这一矛盾,充分发挥道路网络的多路连通效用,使交通网络上的交通流达到基本均衡状态[6],有必要将部分交通外部成本内部化.引入交通“拥挤费”、增大通过费用μ,可以直接缓解外部成本相对过高的问题.依据出行者与管理方利益共赢的理念,使个体成本总量与社会总成本在交通“拥挤费”费率约束下达到相对差值最小,建立规划模型(3)如下.
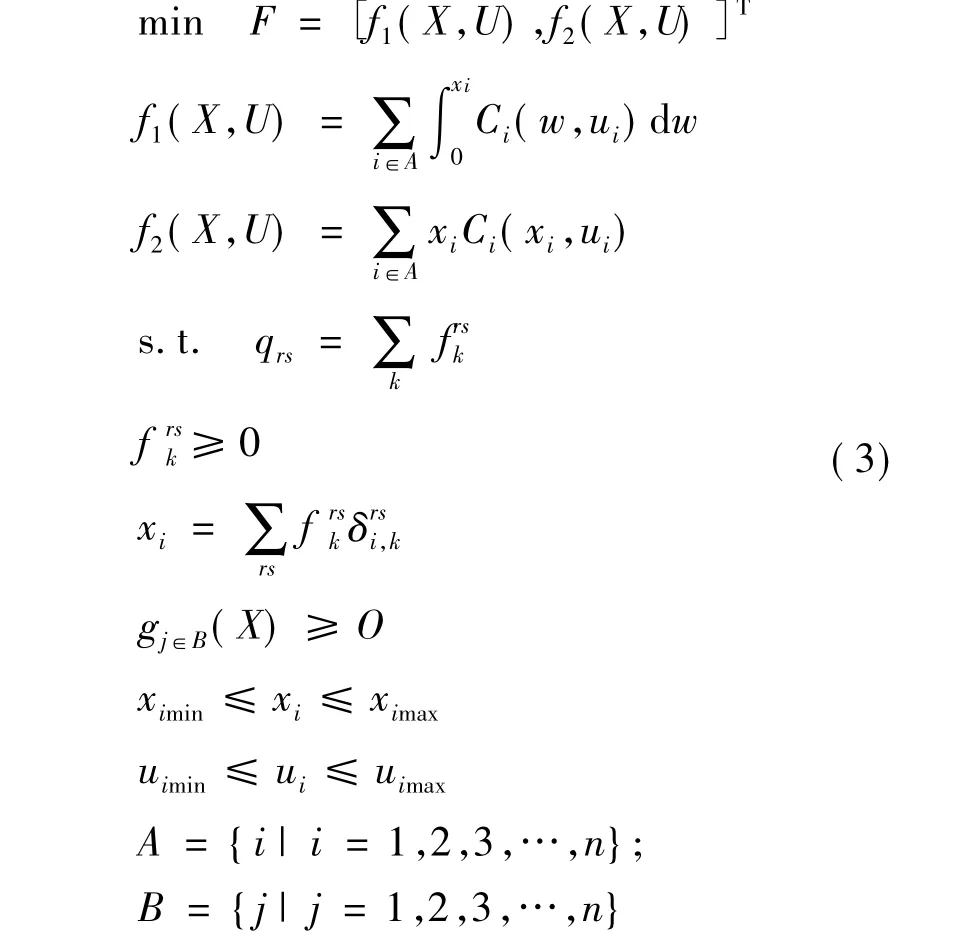
式中,xi为路段i的交通量;ximin为路段i的最小服务交通量;ximax为路段i的最大服务交通量;ui为路段i的拥挤费;uimin为路段i道路管理者所能接受的最小拥挤费;uimax为路段i道路使用者所能接受的最大拥挤费;Ci(xi,ui)为是路段i关于交通量和拥挤费的费用函数,可用交通阻抗函数表示;f1(X,U)为建立在道路使用者主观路线选择行为基础上的个体成本总量;f2(X,U)为建立在管理者系统最优基础上的社会总成本;qrs为OD对(r,s)之间总交通量;为OD对(r,s)之问路径k上的总交通量;为如果路段 i在连接OD对 (r,s)之间路径上,其值为1,否则为0;gj(X)为变量 x1,x2,…,xn之间的联系
2 非线性规划模型算法
由模型(3)可以看出,两个目标函数相互影响、相互制约,出行者的内部成本总量变化趋势并不总与社会出行总成本相一致.为不造成资源浪费、同时保证通过效率,交通网络及其它的交通量分布信息也被列入约束条件之中,模型(3)实际上成为交通网络结构及其交通流量流向分布条件下的、考虑系统与用户利益均衡的交通“拥挤费”决策优化模型.式(2)中的费用转化随机量ε,可由实际情况与环境调查数据的方差决定,亦可按收敛与否、人为试算、合理性判别确定.ε的不同选值,效果上影响到交通“拥挤费”征收的高低,可作为“拥挤费”的调节参数使用.模型可采用增量系数法[7]计算出最佳交通量分配下的个人成本总量和社会总成本.
算法具体步骤如下:
Step 1 确定精确精度ε=0.1,初始化目标函数个数m=1,路段i=0,迭代次数s=1.转step1;
Step 2 对于双目标优化函数优化问题(1),计算第m个目标函数fm(X)的最优解和最优值.令(X)为第m个目标函数在约束集合R内的最优值,=(xm,1,xm,2,…,xm,n)是第 m 个目标函数的最优解.令m=m+1,得到下一个目标函数的最优解和最优值,分别表示为=(xm+1,1,xm+2,1,…,xm+1,n)和(X).转step 3;
3 案例
路网结构如图2所示,由2个节点,一个 OD对,2条路段组成.路线为单向,其中路径1道路等级高,行程距离长,路段2道路等级低,行程距离短.其中已知总交通流量为20 pcu/h,路径1最大服务交通量18 pcu/h,路径2最大服务交通量15 pcu/h.不考虑随机因子,取ε=0(不影响问题说明).正常情况下,行程时间C1(x1,u1)=4x1+u1,C2(x2,u2)=(2x2+u2)2.试采用在路径2 征收拥堵费u重新分配交通量.

图2 OD网络图
路径1和路径2的阻抗都是随着交通量的增大而增大,但OD对间的交通量相对比较稳定.显然随着路径2交通量的增加,路径1的交通量会减少,路径2的阻抗小于路径1.协调控制既不能让路径1的通过能力过度空置,也不能因为2的行程距离短造成拥堵.本例给出的阻抗函数是单调递增的,不考虑拥堵时流量减小的情况,为缓解路径2的交通拥堵并发挥路段2最大交通效益,欲为路径2设一收费站,具体规划模型如下.
建立模型:

利用增量系数法求解多目标优化问题,得到如表1所示的计算结果.不难看出,不收拥堵费时外部成本较高,社会总成本远大于个人成本总量.拥堵费征收增加,个人成本总量也随之上升,但相对于个人成本总量,社会总成本增长缓慢.这表明在一般情况下,社会总成本的变化率总是小于个人成本总量的变化率,社会总成本与个人成本总量完全可以通过不太高的交通收费达到平衡.图3表达了不同拥挤收费率情况下的个人成本总量与社会总成本间的变化关系.当拥堵费征收较少时(小于图中A点坐标),社会总成本高于个人成本总量,出行者欠付交通平衡费,当拥挤费较高时,个人成本总量高于社会总成本,出行者超额支付,个人成本总量与社会总成本增长曲线的交点A即为收费平衡点.拥堵费的征收缓解了外部成本的过大偏置,当社会总成本与个人成本总量相等时,外部成本为零.

表1 相同流量不同路径对于征收不同拥堵费的敏感度分析
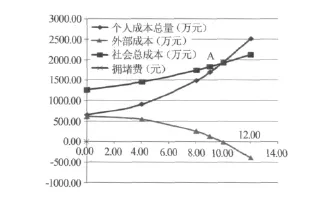
图3 不同拥挤费下目标函数值的变化图
考查本文模型的优化水平,与其他优化方式进行比较.选择方案一为用户均衡UE优化的交通配流模型;方案二为用户和系统共同优化,不考虑收费措施的配流模型;方案三为本文用户系统共同优化的收费模型,其比较结果见表2.对应三种方案,计算外部成本分别为 1 533.33,610.94和0.9,方案三最小.表明与对照的两个方案比较,本文模型较好地平衡了个人内部成本总量与外部总成本,基本达到了合理征收交通“拥挤费”的目标.在合理收费条件下,交通流量的分配也依据道路的实际状况更加趋于合理.

表2 各方案优化效果对比图
4 结论
拥挤收费是一项十分有效的交通需求管理措施,本文所提出的模型考虑到用户与系统的需求,收费率的确定同时依赖于交通网络的状况和交通需求的状况,个人与社会成本的计算也对模型结果有影响.交通拥挤收费除了可以抑制交通的不必要需求外,验证算例还表明,合理的交通拥挤收费可以较好地分配交通资源,促使交通网络达到更好的平衡.由于社会的巨大容量,社会成本的变化大大低于个人成本变化的速率,这使得征收较少量额的交通拥挤费就可以达到外部成本为零的目标成为可能.模型计算对比结果还表明,一项好的交通政策不仅仅只须满足Wordrop第一原理或第二原理,还需要兼顾管理者(社会)与用户(个人)双方的利益.正确地描述和表达各方权益才能取得良好的效果,交通拥挤费率的确定也是如此.
[1]MARTIN J,BECKMANN C B,MCGUIRE,et al.Studies in the Economics of Transportation[M].City of New Haven:Yale university press,1956.
[2]李斌,黄海军.新加坡道路收费系统的实践和经验[J].公路交通科技,2000,6(3):59-62.
[3]李志纯,谷强,史峰.弹性需求下拥挤道路收费的模型与算法研究[J].交通运输工程,2001,1(3):81-85.
[4]郭瑞军,王晚香.城市交通拥挤的社会成本分析初探[J].城市公共交通,2008(4):26-29.
[5]张琳琪,宋瑞,许旺土.拥挤收费对用户均衡交通配流的影响分析[C].2008第四届中国智能交通年会论文集,2008:559-562.
[6]杨兆升.交通运输系统规划[M].北京:人民交通出版社,1998.
[7]余俊,廖道训.最优化及其应用[M].武汉:华中工学院出版社,1983.

