磁悬浮陀螺寻北仪信号去噪方法

王 亮，谭立龙，仲启媛

(第二炮兵工程大学 二系，西安 710025)

采集到的磁浮寻北仪信号受到陀螺漂移、采样电路噪声等污染，需要在信号去噪后才可用来北向解算，从而提高寻北精度。基于傅里叶变换的传统滤波器对广义平稳信号去噪有较好的效果，但它是完全在频域对信号进行分析，不适用于非平稳信号的去噪。小波分析思想的基础是傅里叶变换，它克服傅里叶变换缺少时域分析的不足，是一种窗口大小可改变的时频局部分析方法［1-4］，其显著特点是具备多分辨分析的特性，因此，小波分析素有“数学显微镜”［5］的美誉。

1 Mallat 算法

小波分析依据Mallat［6］分解与重构算法将含噪信号分解成主要部分(低频)和细节部分(高频)。

分解算法:

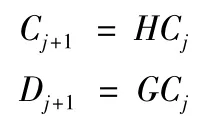
其中:Cj和Dj分别是尺度j 上的逼近系数和小波系数的列阵形式;H 和G 称为滤波器系数矩阵。将低频信号Cj分解成低频信号Cj+1和高频信号Dj+1，并且每次分解过程可以看成是对低频信号的分解。相应的重构算法是分解的逆运算。

重构过程:

其中H*和G*分别是H 和G 的共轭转置矩阵，有

只有正交小波才满足上述重构公式，对于其他非正交小波而言，重构公式为

其中Hl和Gl为综合滤波器，且满足

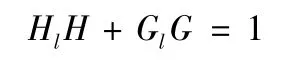
分解与重构过程(k 为分解层次)如图1、2 所示。

2 阈值去噪

在对含噪的寻北仪信号作小波分解后，对小波系数(高频部分)设置阈值。大于该阈值的小波系数表明是真实信号，予以保留;小于该阈值的小波系数是噪声信号，置零后予以去除。

2.1 阈值选取

软阈值去噪和硬阈值去噪是阈值去噪最简单的2 种方法，主要适用于信号中混有白噪声的情况［7-8］。采用软阈值处理的数据没有不连续点，处理后的信号较平滑，在小波去噪方法中最常用。软阈值函数(图3)为

小波阈值去噪方法阈值函数选取后，需要选择合适的阈值大小才能去除噪声，提高信噪比。如果阈值太小，噪声不能完全消除;如果阈值太大，有用信号则被过多的消除。常用的经典阈值法中:Visushrink 阈值法适应多维独立正态变量联合分布，信号的长度决定阈值选取，实际效果不好;SUREShink 阈值估计方法是均方差准则的无偏估计，是专门针对软阈值函数得出的，是理想阈值方法;GCV 阈值也是软阈值函数的去噪方法，是渐近最优阈值，不需要估计噪声的方差，可以获得较好的去噪效果。

2.2 信号处理

在实际的消噪处理过程中，阈值往往可以通过经验公式获得，但在陀螺寻北仪数据处理中没有经验公式可供参考，无法获得给定的阈值，只有采用实验室环境下采集的信号［9-10］。用db10 小波基在不同分解层次上进行软硬阈值消噪法，并与傅里叶变换消噪的效果进行对比，可以看出傅里叶变换消噪的效果不理想，阈值去噪效果优于傅里叶变换去噪。图5 是加汉宁窗的去噪效果。图6 采用db20 小波6 层分解和Bior3 .7 小波6 层分解软或硬阈值消噪后的信号对比。图7 中粗线为软阈值消噪，细线为硬阈值消噪。通过对比，用硬阈值处理后的信号更为粗糙，而软阈值处理的信号很光滑.实践证明，软阈值能较好的消除信号中的噪声，适用于处理磁悬浮寻北仪的信号去噪。

3 模极大值去噪

模极大值法寻找每级尺度上小波变换系数对应的模极大值点。若随着分解尺度j 的增大，对应的模极大值也增大，则此模极大值是由信号点的小波系数得到的，应保留;若随着分解尺度j 的增大，对应的模极大值减小，则此模极大值是由噪声点的小波系数得到的，应该滤除。

采用分段三次样条插值算法［7］进行小波系数的重构，并在插值之前先对模极大值进行预处理，由此得到了一组新的伪模极大值序列，保证通过这些伪模极大值点模拟出来的小波变换函数在给定处且仅在这些点具有模极大值。

在检测陀螺仪输出信号突变时，短的小波通常比长的小波更有效。通过最小的小波辨识不连续性的形状比用最长的小波做同样的处理更为简单。因此，由于辨识信号的不连续性，只使用harr 小波就足够了。辨识j 阶导数的不连续性，需选择至少具有j 阶消失矩的正则小波。

图8 是一次采样数据采用db3 小波进行在不同尺度下的模极大值。图9 是模极大值消噪效果。从图中可以看出，绝大部分噪声被消除，而干扰的信号特征得到有效保留。图8 中还可看出小波分析相对傅里叶分析的一个很重要的优势，如果用傅里叶变换处理这个信号，就不能精确地定位故障发生的位置，因为在傅里叶分析中不可能同时看到频率的变化和时域变化发生的位置。

4 结束语

阈值去噪和模极大值的去噪效果优于基于傅里叶变换的数字滤波。阈值去噪是小波去噪中常用的方法，对磁悬浮寻北仪信号的去噪效果理想。在实际应用中，可以依据不同的信号形式和不同的噪声强度，选取相应的小波在不同的分解层次进行去噪。阈值去噪既改善了信噪比，又不引起波形的较大失真，有很强的抗干扰性。

模极大值去噪依据真实信号的小波系数模极大值随着分解层次的增加而增大，噪声信号的小波系数模极大值随着分解层增大而减小，这一特性可以有效去除寻北仪噪声信号。在利用小波模极值去噪时，小波分解尺度过小，小波系数受噪声影响非常大，产生许多伪极值点，而尺度过大会使信号丢失某些重要的局部奇异性，因此需要选择合适的尺度。如何针对信噪比自适应地确定小波分解层数，进一步提高寻北仪信号消噪的效率是下一步研究的方向。

［1］成礼智，王红霞，罗永，等. 小波的理论与应用［M］. 北京:科学出版社，2006.

［2］司祯祯.傅里叶变换与小波在信号去噪中的应用［J］.电子设计工程，2011，19(4):155-157.

［3］赵松.基于改进小波阈值函数的雷达信号去噪［J］.兵工自动化，2011(7):1-3.

［4］杜林，周新明，李征，等.一种基于小波变换的自适应阈值图像去噪方法［J］.数字通信，2010(2):55-57.

［5］杨福生. 小波分析算法与应用［M］. 北京:科学出版社，2000.

［6］Mallat S.A theory of multire solution signal decomposition:the wavelet representation［J］.IEEE Trans On PAMI，1989，11(7):674-691.

［7］边威.小波基的选取与构造方法讨论［D］.长春:东北师范大学，2007.

［8］陈慧慧，郑宾.基于小波模极大值的自动机信号降噪方法［J］.机械工程与自动化，2010(5):36-37.

［9］汪小梅，朱华.一种改进的小波变换阈值去噪法［J］.重庆理工大学学报:自然科学版，2010(6):48-51.

［10］夏敏华.3 mm 波段脉冲雷达系统研究和小波去噪分析［D］.南京:南京理工大学，2004.