航空弹药随机存储策略模型
朱来辉,曹 炜,张 珏
(1.桂林空军学院 广州训练大队,广州 510000;2.广空装备部军通处,广州 510071)
航空弹药的消耗量是影响航空弹药订货的重要因素,在和平时期,航空弹药的消耗量是可预见和可计划的,因此,在本文中应用航空弹药随机存贮策略采用(s,S)策略,其中s是航空弹药的最佳库存控制水平,S 是最大消耗水平的上限,若无法确定最大消耗上限,则S 应该确定为大于s 的某个具体值。建立本模型的目标是满足军事要求的情况下使总相关费用最小[1-6]。
1 模型假设
模型假设[6,7]:
1)在本模型中,考虑订货费、贮存费和每种航空弹药的进货价格、缺货损失等。为衡量航空弹药的供应情况,引入供应信度、失供概率等概念。
2)一般来说某种弹药的单位贮存费与贮存时间有关,为简化计算,假设在一个存储周期内,某种弹药的单位贮存费用不变。
3)每次使用的都是贮存时间最长的弹药,保证存储的都是较新的弹药;且消耗满足一定的概率分布。
2 模型建立与求解
(s,S)储存策略,即采用连续盘点的库存检查方式,当库存水平高于s 时,不进行订货;当库存水平低于s 时,进行订货,并将库存水平补充至S。
2.1 模型符号说明:
Y 表示所有航空弹药仓库总费用;
Yij表示第i 个航空弹药仓库第j 种弹药在一个周期内的总费用;
Tij表示存储周期;
Zij表示第i 个航空弹药仓库第j 种弹药在一个存储周期内可能的战役需求量与训练需求量之和;
rij表示第i 个航空弹药仓库第j 种弹药在一个周期内的需求量;
f(rij)表示第i 个航空弹药仓库第j 种弹药在一个周期内的需求概率密度;
cij表示第i 个航空弹药仓库第j 种弹药订货的单位价格;
lij表示第i 个航空弹药仓库第j 种弹药每次的订货费用;
qij表示第i 个航空弹药仓库第j 种弹药在一个周期内的单位存贮费用;
Qij表示第i 个航空弹药仓库第j 种弹药在一个存贮周期的总费用;
xij表示第i 个航空弹药仓库第j 种弹药在一个周期内的订货量;
m 表示总仓库数;
n 表示总弹药种类;
sij表示第i 个航空弹药仓库第j 种弹药库存水平下限;
Sij表示第i 个航空弹药仓库第j 种弹药库存水平上限;
uij表示第i 个航空弹药仓库第j 种弹药的供应信度;
kij表示在盘点时第i 个航空弹药仓库第j 种弹药的剩余量;
uij表示第i 个航空弹药仓库第j 种弹药单位缺货损失费用。
2.2 模型建立
目标函数:
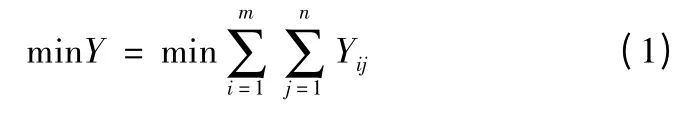
其中
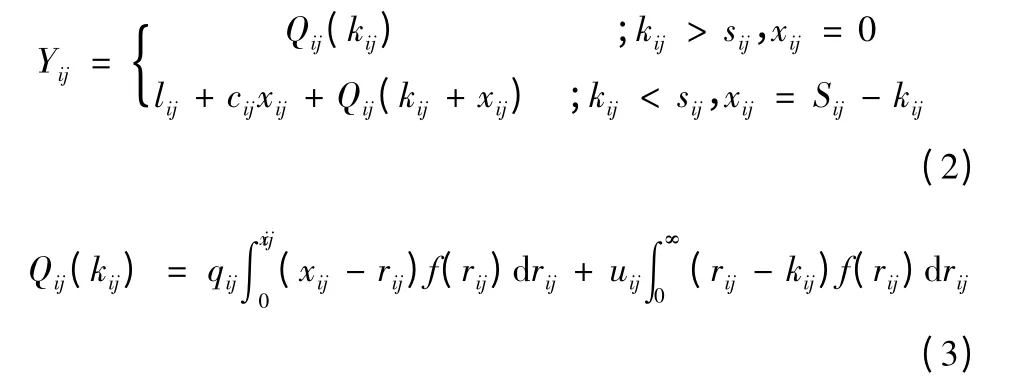
约束条件:

0.95是一般取值[7]。

2.3 模型求解
本模型中,最重要的是确定Sij和sij。
2.3.1 Sij的确定
当kij<sij时,求xij使Yij达到最小值,由此就可确定Sij。
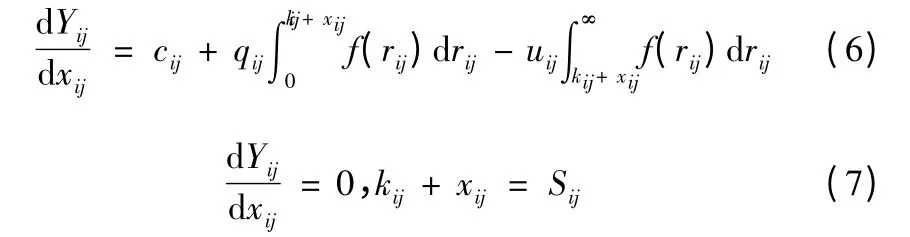
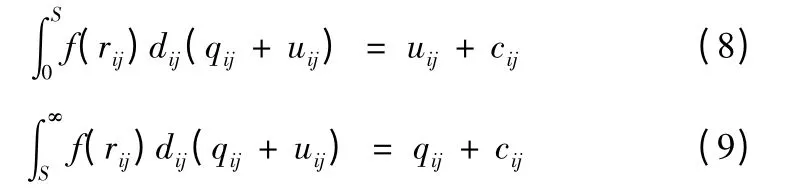
综合以上公式,得
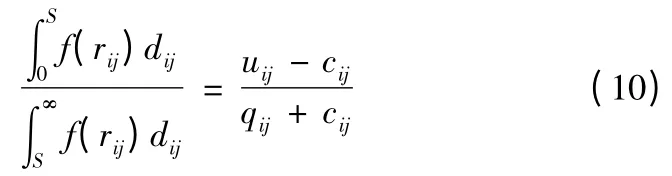
由以上模型可得,当每种航空弹药的单位价格cij一定时,贮存费qij越小,缺货费用越大,则Sij应越大。根据航空弹药实际情况,综合约束条件,就可确定Sij的实际值。
2.3.2 sij的确定
当第i 个航空弹药仓库第j 种弹药存货量为kij时,如果订货,则将航空弹药的存储水平补充至Sij。因此可得此种航空弹药在一个存储周期的平均花费为
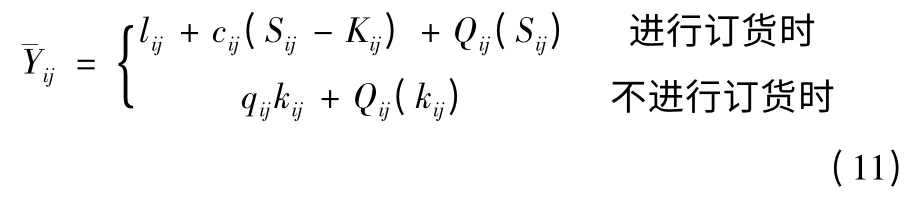
不进行订货时与订货时的花费相比较,应满足
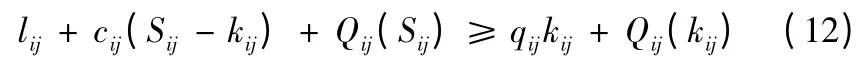
令M(x)=qijxij+Qij(xij),则有
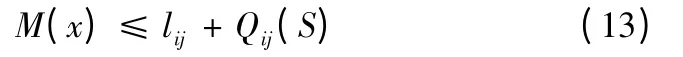
因此s 应为方程M(x)=lij+Qij(S)最小正根。利用图形求解得,在xij=S 时M(x)取得最小值,在极小值上叠加lij,对应的xij值即是s 值,如图1 所示。
综合各方程可得,当cij,f(rij),lij,qij,uij确定后,就可确定s,S 的值。在实际计算时,可用计算机编程,采用如智能优化算法、进化策略[7,8]等对模型进行求解。以上得出的仅仅是满足数学意义上的s,S 值,在实际应用中,还应满足约束条件
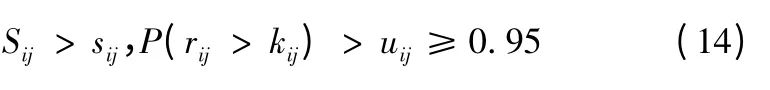
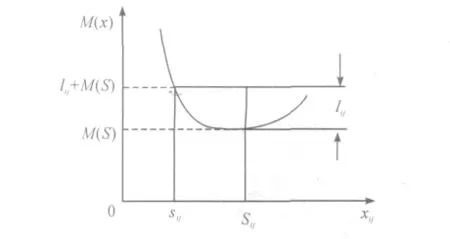
图1 求s 的图解法
3 结束语
本模型从实际出发,通过确定s、S 值,使总相关费用最小,对航空弹药的存储决策有一定的参考作用。特别说明的是,本模型建立的前提是允许缺货,但是把弹药的供应信度设定的较高(0.95)。战时情况特殊,如不允许缺货时,则uij将变为无穷大,则S 值也变为无穷大,由于库容有限,这是不可能的。应根据实际情况,将各个评定的航空弹药仓库储存尽可能多的弹药,这是战时的存储策略。
[1]邢世忠,陈达植,张伟业,等.军事装备学[M].北京:国防大学出版社,2000.
[2]空军装备部.航空弹药订货与储备结构预测方法研究[Z].北京:空军装备部,2005.
[3]龚传信.装备勤务学[M].石家庄:军械工程学院,2001.
[4]陈学广,徐维江.弹药保障决策模型的研究[J].军械工程学院学报,2001,13(3):52-55.
[5]邱鹞荀,烨孙志,刚马妍.军队战备物资储备结构优化模型研究[J].军事交通学院学报,2009,11(2):73-76.
[6]付向红.交货时间为随机变量的存储模型[J].重庆文理学院学报:自然科学版,2009,28(2):41- 43.
[7]刘金梅.航空弹药供应保障决策支持系统研究[D].南京:南京理工大学,2006.
[8]瞿高峰,陈淑燕. 基于进化策略的随机存储模型求解[J].东北师大学报:自然科学版,2003,35(4):14-18.

