新型弯张换能器——欧米伽换能器频率特性与形状参数关系

王雨虹

(海军工程大学 兵器工程系，武汉 430033)

在水声探测领域，为了达到探测更远、占用载体空间更小、质量更小的目的，声呐换能器需要向低频、小尺寸和小质量的方向发展，人们在换能器材料、致声机理［1-2］、换能器结构等方面进行了不懈的探索。弯张换能器就是其中的一类，弯张换能器目前已经发展出7 种，分别侧重于满足某一项或几项需求，钹式换能器就是其中的一种，钹式换能器最初用来作为高灵敏度的水听器和微执行器［3-5］。钹式换能器为了克服Moonie 换能器端帽上的轴向位移量不均匀，且在粘结层上的较厚的端帽中有较大的应力聚集的缺点而出现，钹式换能器具有体积小、重量轻，能产生较大的位移、速度、加速度，并具有较大的动态范围等优点［6-8］。经过发展改进，它还可作为水声发射换能器、动态压力传感器和加速度传感器使用［9-11］。作者设计了一种新型弯张换能器—欧米伽换能器，在相同大小的情况下，发现它比钹式换能器具有更好的低频性能和接收灵敏度。本文主要从欧米伽换能器的空腔底部半径、空腔顶部半径、空腔高度、陶瓷片厚度和金属片厚度与欧米伽换能器的基频、频带宽度、机械品质因数和接收灵敏度之间的对应关系进行研究。

1 欧米伽换能器结构与原理

图1 是欧米伽换能器的结构原理图。其中Tp指压电陶瓷片厚度，Tc指金属片厚度，Rc指换能器空腔顶部半径，Rp指空腔底部半径，H 指换能器空腔高度，R 指换能器压电陶瓷片半径。如图1 所示，该新型换能器是一种将金属帽、压电陶瓷圆片用环氧树脂粘结复合制成弯张换能器。从外形上看，该换能器的上下两半部分均像希腊大写字母“Ω”而被本文作者命名。与钹式换能器一样，该换能器的金属帽与压电陶瓷片通过耦合改变压电陶瓷的应力分布，并将径向应力转变为轴向应力，具有较大的位移放大作用，该换能器的压电响应与相同尺寸PZT 压电陶资片相比也有较大提高。与钹式换能器不同的是，此设计的一个明显优点是压电陶瓷片和金属端帽同相振动，消除了辐射场中的所有反相分量，而钹式换能器的陶瓷片和金属端帽则呈反相振动。其次，欧米伽换能器的制作工艺要比钹式换能器要复杂，这是该换能器的缺点之一。

本文采用ANSYS 软件对欧米伽换能器进行分析，所需的基本方程有［12］:

其中，式(1)是结构分析方程，式(2)是压电分析方程，式(3)是流固耦合方程。在方程(1)中，［M］、［C］和［K］分别是系统的质量矩阵、阻尼矩阵和刚度矩阵。通过施加载荷力向量{F} ，计算出位移向量{u}便是结构问题的解。方程(2)将压电体节点电势向量{V} 与位移向量{u} 组合成广义的位移向量，将节点电量向量{Q}和载荷力向量和{F} 组合成广义载荷向量;广义质量阵与广义阻尼矩阵中以［0］扩充，在广义刚度阵中加入机电耦合分量［Kds］和介电矩阵分量［Kd］。方程(3)在流体—结构界面上直接进行流固耦合，将节点声压向量{p}与结构位移向量{u}组合成，而在广义质量阵、广义刚度阵中加入流体—结构耦合分量［Kfs］与［Mfs］，分别用脚标f 和s 代表流体与结构。

图1 欧米伽换能器的结构原理

接收灵敏度［12］:

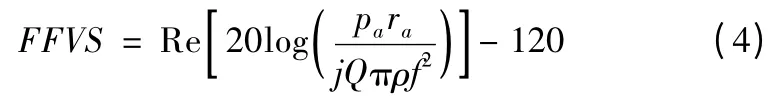
其中:pa指距离换能器中心ra处的声压;Q 指ANSYS 后处理器中在正电极电压耦合部中选取节点序号最低节点的电荷值;Re［］指取实部运算。需要说明的是，计算结果中的频带宽度指接收灵敏度的-3 dB 带宽，机械品质因数也用该带宽计算。采用PZT5H 材料，金属端帽为黄铜，并采用参考文献［13］与［14］的相关参数。

2 欧米伽换能器频率特性与形状参数关系

2.1 频率特性与空腔顶部半径的关系

本节除空腔顶部半径Rc外，其余参数为:空腔高度H=3.4 mm，压电陶瓷片半径R=12 mm，空腔底部半径Rp=9.6 mm，金属片厚度Tc=0.2 mm，压电陶瓷片厚度Tp=1 mm。随着空腔顶部半径Rc从10.5 mm 增加到23 mm:从图2(a)可以看出，第1 阶谐振频率即基频f 从1 224 Hz 下降到184 Hz，且下降趋势渐趋平缓。从图2(b)可以看出，频带宽度Δf 从164.9 Hz 逐渐下降到17.2 Hz，下降趋势也越来越平缓。从图2(c)可知，机械品质因数Qm为上升趋势，在10 mm 到12 mm 之间起始阶段的上升趋势非常明显，以后的上升趋势较为缓慢，中间略有起伏，起伏幅度小于0.3，起伏的原因主要是:计算所取的频率间隔较大和网格划分不够精细，导致频带宽度Δf 和基频f 计算的不准确，引起一定程度的起伏。从图2(d)可以看出，它的接收灵敏度FFVS 类似抛物线式单调增加，最后达到-160 dB 左右。从整体来看，空腔顶部半径Rc的变化对基频f、频带宽度Δf、机械品质因数Qm和接收灵敏度FFVS 的影响均较为显著。

图2 欧米伽换能器频率特性与空腔顶部半径Rc 之间的关系

2.2 频率特性与空腔高度的关系

本节除空腔高度H 外，其余参数为:空腔顶部半径Rc=17 mm，压电陶瓷片半径R =12 mm，空腔底部半径Rp=9.6 mm，金属片厚度Tc=0.2 mm，压电陶瓷片厚度Tp=1 mm。随着空腔高度H 从1.3 mm 增加到5.3 mm:由图3(a)可知，基频f 也逐渐从360 Hz 升高到395 Hz，增加35 Hz。由图3(b)可知，频带宽度Δf 从33.6 Hz 增加到37.5 Hz，增加不到4 Hz。由图3(c)可知，机械品质因数Qm在10.53 和10.71 之间变化，且整个变化趋势不明显。由图3(d)可知，接收灵敏度FFVS 从-158.0 dB 下降到-171.7 dB。因此，从整体上来讲，随着空腔高度H 的增加，接收灵敏度FFVS 有显著的减小趋势，而空腔高度H 的变化对基频f、频带宽度Δf 和机械品质因数Qm的影响较小，对应关系相对较弱。

2.3 频率特性与空腔底部半径的关系

本节除空腔底部半径Rp外，其余参数为:空腔高度H=3.4 mm，空腔顶部半径Rc=17 mm，金属片厚度Tc=0.2 mm，压电陶瓷片厚度Tp=1 mm，随着空腔底部半径Rp的变化，压电陶瓷片半径R 也随着调整，且满足关系式R -Rp=2.4 mm。随着空腔底部半径Rp从2 mm 增加到11.7 mm:由图4(a)可知，基频f 从510 Hz 增加到530 Hz，增加20 Hz，增加幅度较小，说明空腔底部半径Rp对基频f 的影响有限。由图4(b)可知，频带宽度Δf 在49.3 Hz 和51.9 Hz 之间不到3 Hz 的范围内变化，可见，频带宽度Δf 与空腔底部半径Rp的对应关系不明显。由图4(c)可知，机械品质因数Qm在10.3 到10.4 之间不到0.1 的范围内变化，也说明机械品质因数Qm与空腔底部半径Rp的对应关系较弱。由图4(d)可知，接收灵敏度H 在空腔底部半径Rp=6 mm 时达到最大值，变化规律与开口向下的抛物线形状类似。总体上来说，空腔底部半径Rp对接收灵敏度Rp的影响较大，且有极值存在，对基频Tc、频带宽度Δf、和机械品质因数Qm的影响较小。

2.4 频率特性与陶瓷片厚度的关系

本节除压电陶瓷片的厚度Tp外，其余参数为:空腔高度H=3.4 mm，空腔顶部半径Rc=17 mm，压电陶瓷片半径R=12 mm，金属片厚度Tc=0. 2 mm，空腔底部半径Rp=9. 6 mm。随着陶瓷片厚度Tp从0.4 mm 增加到3 mm:由图5(a)可知，基频f 基本保持在388 Hz 的频率点上不变化，或者说变化很小。由图5(b)可知，频带宽度Δf 在36.6 Hz 与36.8 Hz 之间0.2 Hz 的范围内变化。由图5(c)可知，机械品质因数Qm在10.55 与10.61 之间0.06 Hz 的范围内变化。由图由图5(d)可知，在陶瓷片厚度Tp=1.8 mm 时，接收灵敏度FFVS 达到最大值-165.6 dB，在陶瓷片厚度Tp从0.4 mm增加到1.8 mm 时，接收灵敏度FFVS 增加速度较快，以后则较为缓慢地下降。总体上来讲，陶瓷片厚度Rp对基频f、频带宽度Δf 和机械品质因数Qm的影响微弱，而对接收灵敏度FFVS 的影响较为显著，且有极大值存在。

2.5 频率特性与金属片厚度的关系

本节除金属片厚度Tc外，其余参数如为:空腔高度H =3.8 mm，空腔顶部半径Rc=17 mm，压电陶瓷片半径R =12.4 mm，压电陶瓷片厚度Tp=1 mm，空腔底部半径Rp=9.6 mm。随着金属片厚度Tc从0.1 mm 增加到1 mm:由图6(a)可知，基频f 从152 Hz 增加到2 944 Hz，基本上成线性增加。由图6(b)可知，频带宽度Δf 从14 Hz 以抛物线方式增加到400 Hz。由图6(c)可知，机械品质因数Qm在7.3 与11.2 的范围内逐渐减小。由图6(d)可知，在金属片厚度Tc=0.2 mm 时，接收灵敏度FFVS 达到最大值-167.2 dB，接收灵敏度的变化类似于抛物线形。总体上来讲，金属片厚度Tc对基频f、频带宽度Δf 和机械品质因数Qm和接收灵敏度FFVS的影响均较大，且接收灵敏度FFVS 有极大值存在。

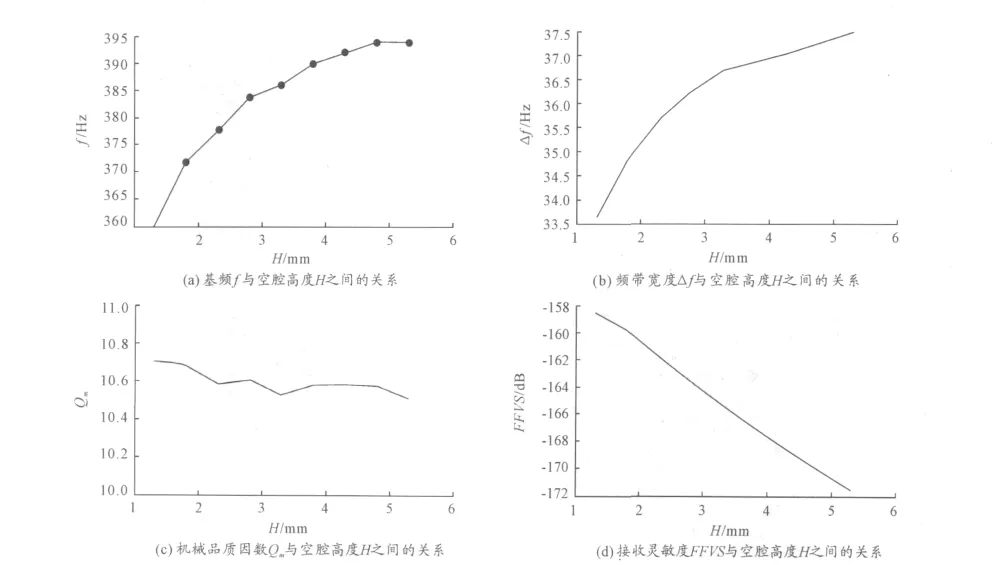
图3 欧米伽换能器频率特性与空腔高度H 之间的关系

图6 欧米伽换能器频率特性与金属片厚度Tc 之间的关系

3 结论

欧米伽换能器形状参数的任何一项发生变化，它的频率特性就会产生相应的变化，一种指标的变好，可能意味着另外一种指标的变差，需要进行综合考虑以满足不同的需求。对基频影响显著的参数主要是欧米伽换能器的空腔顶部半径和金属片厚度，因此，如果需要得到较低基频的欧米伽换能器，最方便的办法是增加空腔顶部半径或者减小金属片厚度，或者两者综合运用。接收灵敏度受空腔顶部半径、空腔高度、空腔底部半径、金属片厚度的影响均较大，且有极大值存在。在满足频率要求的情况下，可以通过减小空腔高度、选择合适的陶瓷片厚度和空腔底部半径等综合措施提高接收灵敏度。频带宽度会随着基频的增加而增加，而机械品质因数则会出现减小的趋势。

［1］王雨虹，王江安，宗思光，等.激光致声声呐换能器设计［J］.声学学报，2008，33(6):562-565.

［2］王雨虹，王江安，吴荣华.透明液体中激光致声特性［J］.计算物理，2010，27(2):257-262.

［3］Tressler J F，Cao W W，Uchino K，Newnham R E.Finite Element Analysis of the Cymbal-Type Flextensional Transducer［J］. IEEE transactions on ultrasonics，ferroelectrics，and frequency control，2000，45(5):1363-1369.

［4］Xu Q C，Yoshikawa S，Belsick J R，Newnham R E.Piezoelectric composites with high sensitivity and high capacitance for use at high pressures［J］.IEEE transactions on ultrasonics，ferroelectrics，and frequency control，1991，38(6):634-639.

［5］Dogan A，Uchino K，Newnham R E.Composite piezoelectric transducer with truncated conical endcaps“cymbal”［J］.IEEE transactions on ultrasonics，ferroelectrics，and frequency control，1997，44(3):597-605.

［6］王suka K，Dogan A，Tressler J F.Metal-Ceramic Composite Transducer:the‘Moonie’［J］.Journal of Intelligent Material Systems and Structrues，1995，6(4):447-455.

［8］Zhang J D，Hughes W J，Meyer R J，et al.A Class V Flextensional Transducer:the Cymbal［J］. Ultrasonics，1999，37(6):387-393.

［9］林书玉，许龙.一种新型Cymbal 换能器的研究［J］.声学学报，2011，36(1):27-36.

［10］Newnham R E，Dogen A.Metal-electroactive ceramic composite transducer.U.S.Patent 5，729，077 (1998).

［11］Fernfindez J F，Dogan A，Fielding J T . Tailoring the performance of ceramic-metal piezocomposite actuators‘cymbals’［J］. Sensors and Actuators，1998，65(2 -3):228-237.

［12］莫喜平.ANSYS 软件在模拟分析声学换能器中的应用［J］.声学技术，2007，26(6):1279-1290.

［13］栾桂东，张金铎，王仁乾.压电换能器和换能器阵［M］.北京:北京大学出版社，2005:93-95.

［14］王荣津.水声材料手册［M］.北京:科学出版社，1983:86-147.