导弹控制系统仿真基本方法
杨育荣,王建琦,2
(1.中国空空导弹研究院,河南 洛阳 471009;2.航空制导武器航空科技重点实验室,河南 洛阳 471009)
数字仿真是将实际系统中的各组成部分全部用数学模型代替,并把数学模型转换成数字仿真模型,在数字计算机上对实际系统进行仿真研究的过程。它具有如下特点:①经济性,不需要实物的参与,是最经济的研究方法;②灵活性,控制系统的研制是不断完善的过程,如果对产品硬件进行修改,无疑费时费力,而利用数字仿真,通过对数学模型进行修改,可方便地对制导系统的每一部分进行迭代设计和参数优化,更具灵活性,并大大缩短研制周期[1-2];③通用性,既往型号数学仿真中建立的数学模型经过少许的改进和开发,可以适用于后续型号或派生型号的研究。
本文主要介绍用泰勒级数对导弹控制系统数字仿真的模型化方法,对导弹控制系统数字仿真的方法、步骤、内容以及仿真试验的设计等进行详细描述,给出了评价仿真结果的方法。
1 导弹运动方程线性化原理
导弹空间运动通常由一个非线性系数的微分方程组来描述。分析导弹的动态特性,可以采用泰勒级数的线性化方法[3]。假设导弹运动方程为一般形式的微分方程组,即:

式中:f1,f2,…,fn,F1,F2,…,Fn都是关于导弹运动参数x1,x2,…xn的函数。
由理想弹道计算可得其特解为
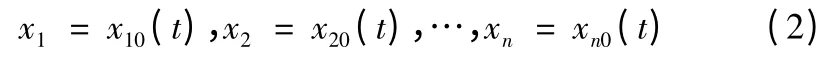
式中下标0 表示基准弹道的参数。将特解式(2)代入式(1)可得

对一般形式的微分方程组(1)进行线性化,为不失代表性,任取一个方程,并省略其下标,有

式中:x 可以代表含扰动作用飞行的任一运动参数,在基准运动中有
一个运动参数在扰动运动和未扰动运动中之差称为运动参数的偏量(或增量),其形式为

令Δx=x-x0,Δf=f-f0,ΔF=F-F0,因此,式(5)可改写为

式(6)又可以改写成

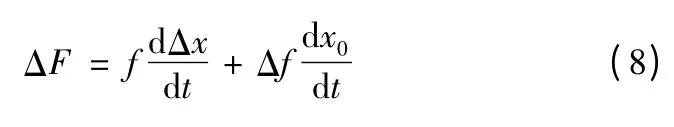
式中:ΔF 和Δf 是函数增量,可由以下方法计算。
将f 在x10,x20,…xn0点附近展开为泰勒级数,且定义f00=f0(x10,x20,…xn0),则有

式中Rf是所有高于二阶以上各项之和。增量函数Δf 为

同理可以求得增量函数ΔF 的表达式为
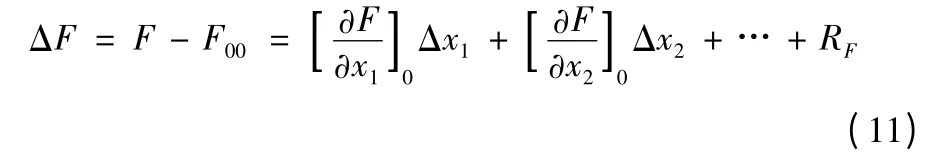
略去高阶小量之和,式(8)可以写为

可得任一运动参数的偏量的线性微分方程式

显然,式(13)中的自变量是运动参数偏量Δx,可以是Δx1,Δx2,…Δxn,偏量在方程式中仅有1 次幂,没有偏量间的乘积,所以微分方程式(12)是线性的。式中,函数f0以及偏导数等,均是已知的基准弹道运动参数的函数。
2 导弹仿真模型的建立
2.1 弹体纵向运动小扰动模型
利用导弹质心动力学、绕质心转动动力学、姿态运动学等方程[4],采用小扰动线性化,忽略二阶以上微量以及导弹气动力、气动力矩的次要因素时,可使方程实现线性化,得到导弹运动的简化方程。由导弹弹体纵向运动方程,采用上述线性化方法,可以得到小扰动模型为:

式中:ϑ 为俯仰角;θ 为弹道倾角;α 为攻角;δ 为舵偏角;a1~a5为弹体动力系数,其计算公式为

其中:q 为动压;Sref为参考面积;m 为质量;V 为速度;Lref为参考长度;Jz为转动惯量为气动偏导数。
2.2 纵向运动传递函数
导弹纵向运动传递函数为:
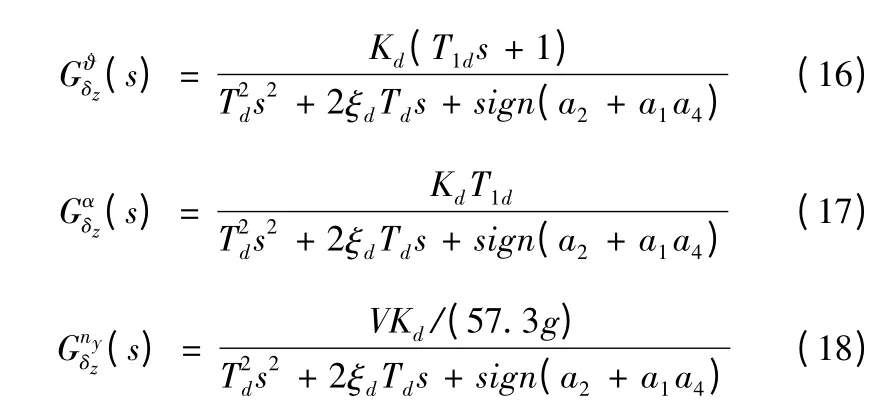
式中传递函数系数计算公式为:

3 导弹控制系统数字仿真
导弹控制系统仿真包括线性化仿真和非线性仿真。线性化仿真是在导弹的飞行空域中,选取特征点,利用固定导弹的飞行高度、马赫数、攻角、发动机燃烧时间等,利用传统的控制理论,来研究导弹的闭环时域特性和开环频域特性[5-6]。
非线性仿真在导弹飞行空域内选取一条特定的弹道进行,其实质为求解高阶微分方程,仿真的基本步骤为:
1)写出实际系统的数学模型;
2)将数学模型二次模型化,转变成可编程的离散化模型;
3)针对离散化模型,用编程语言编写仿真程序;
4)仿真结果分析、修改,直至满足要求。
3.1 线性化仿真
线性化模型是非线性模型的简化,具有模型简单、容易实现等特点,一般考虑连续系统,进行时域分析和频域分析。时域分析对系统施加一定的输入信号,通过研究系统的时间响应来评价系统性能[7]。对三回路自动驾驶仪来说,时域分析主要对角速度回路、姿态角回路和加速度回路进行闭环分析,考察上升时间(tr)、超调量(σp)、稳态误差等指标。图1为某导弹控制系统的阶跃响应曲线。

图1 控制系统阶跃响应曲线
导弹控制系统时域指标一般是上升时间小于0.3 s,超调量小于20%,稳态误差小于10%。从图1 可以看出,系统阶跃响应上升到85%的时间为0.22 s,超调量为1.3%,稳态误差为0,因此图1 的系统能够满足时域设计要求,但仍需要分析其频域特性。
频域分析通过系统开环的频率特性来进行。开环频域特性主要分析幅值裕度(Gm)、相位裕度(Pm)等[8]。图2 所示为图1 中对应的频域特性曲线。

图2 控制系统频域特性曲线
导弹控制系统频域指标一般是幅值裕度大于6 dB,相位裕度大于30 rad/s。从图2 中可以看出,系统的幅值裕度为7.71 dB,相位裕度为34.1 rad/s。因此,此系统满足时域、频域设计要求。
3.2 非线性仿真
现代导弹是一个非常复杂的系统,大攻角、非线性、强耦合等特点决定了导弹控制系统的设计必须要经过严格的考核。控制系统在工作过程中,力系数、力矩系数、转动惯量、推力偏心、推力温度、舵零位误差、舵机前向控制增益、初始俯仰角、初始发射速度等都可能影响其性能。这些因素的排列组合将非常庞大,因此需要寻求一种尽量少做仿真试验但却能全面考核导弹性能的试验方法。非线性仿真可以采用单项因素、机弹干扰和正交拉偏等试验进行[9]。
1)单项因素仿真。只考察某1 个特定参数的影响程度,进行单项因素仿真(包括对这个参数的上拉偏、下拉偏和额定偏仿真)。
2)机弹干扰仿真。在导弹和飞机分离时刻引入1 个初始角速度、攻角、力矩、力等进行发射仿真。
3)正交拉偏仿真。选取n 个不相关的算法影响因素1,2,…,n,每个影响因素有1,2,…,k 个影响水平,需要进行m次试验才能对算法进行全面仿真。针对这个问题可以构造一个正交表Lm(nk)。表1 所示为正交表L9(34),其中行表头表示影响因素,列表头表示试验次数,数字1 表示各因素下拉偏仿真,2 表示额定仿真,3 表示上拉偏仿真。
4 仿真实例
图3 为某次单项因素仿真最大攻角统计曲线。对于图3中的攻角最大限幅到40°。从图3 中可以看出,部分仿真结果达到了限幅值,然而气动数据分析所需要的攻角远小于仿真值,说明在攻角为40°的仿真系统可能已经发散,需要进一步分析;其他条件仿真结果正常。

表1 L9(34)正交试验

从图4 中可以看出,初始时刻导弹具有攻角,引入控制后导弹攻角很快稳定,说明若导弹发射攻角小于等于图4 中的攻角时,系统能够稳定。
图5 所示为某次正交拉偏最大通道舵偏统计曲线。

图5 正交拉偏最大通道舵偏统计曲线
同样对于图5 中的最大舵偏也具有限幅值,在达到限幅值的仿真条件中,由于正常仿真情况下,所需要的舵偏小于仿真值,说明在舵偏限幅的仿真条件处系统可能已经发散,这些发散的条件将是控制系统设计迭代时分析的重点弹道。
5 结束语
导弹在论证、方案、工程研制和定型等阶段,计算机数字仿真是必不可少的技术手段。数字仿真仿真时间短、可重复,可以用来弥补飞行试验数据之不足,既可以缩短研制周期,也可以节省大量经费。本文基于传统的导弹控制系统设计过程,介绍了弹体模型线性化的原理,描述了导弹线性、非线性仿真的基本方法,通过对正交表的描述,介绍了现代导弹控制系统设计过程中所必须的拉偏仿真,并对仿真结果给出了评价的方法。
[1]杨新.飞机六自由度模型及仿真研究[J].系统仿真学报,2000(5):210-213.
[2]谢晓方,李松阳,孙涛.导弹通用武器控制系统体系结构研究[J].兵工自动化,2010(1):1-4.
[3]张有济.战术导弹飞行力学设计[M].北京:宇航出版社,1998.
[4]胡小平,吴美平,王海丽.导弹飞行力学基础[M].北京:国防科技大学出版社,2006.
[5]刘真,张涛.基于H∞混合灵敏度的导弹稳定控制回路设计[J].四川兵工学报,2011(7):40-43.
[6]伍晓军,李翊,孙晓燕,等.基于攻角力测的不确定导弹系统的滑模自适应控制研究[J].海军航空工程学院学报,2011(4):410-413.
[7]Bernstein D S.The treatment of inputs in real-time digital simulation[J].Simulation,1979,33(2):65-68.
[8]Lambert J D.Computational methods in ordinary differential equations[M].New York:Wiley,1973.
[9]刘瑞叶,任洪林,李志民.计算机仿真技术基础[M].北京:电子工业出版社,2004.
[10]许志,林永生,解永锋,等.基于RTX 的空面导弹制导控制系统快速原型仿真[J].火力与指挥控制,2010(12):184-187.

