基于信息熵的传感器多目标信息探测算法

2012-07-02 00:51汪高武

兵器装备工程学报 2012年7期

汪高武

(中船重工第七一六研究所，江苏连云港 222006)

传感器多目标信息探测是通过对传感器系统进行优化分配和工作模式设定，以使系统尽可能多地获得环境中存在的目标的信息。传感器多目标信息探测的实质是一个优化问题。早期的优化对象是运动学中的数据，但是这种优化算法仅考虑了目标运动的因素，而没有考虑传感器探测和识别等因素。例如，利用卡尔曼滤波估计目标的未来位置，通过目标位置的方差控制传感器的采样频率就属于这类优化算法。这类算法很难控制传感器工作模式(探测、跟踪和识别)的转换，并且难以实现对一组传感器同时进行优化分配。后来的优化对象综合考虑了动力学中的数据和传感器工作模式等因素。为综合考虑多个因素，实现传感器多目标信息探测的优化，许多专家提出了信息论的方法。本文利用信息增量进行传感器多目标信息探测，提出了基于信息增量的传感器多目标信息探测算法。

1 信息熵和信息增量

1948年，香浓将热力学的熵引入到信息论，因此信息熵(Information entropy)又被称为香浓熵(Shannon entropy)。信息论中，熵被用来衡量一个随机变量出现的期望值。它代表被接受之前信号传输过程中损失的信息量。信息熵也称信源熵、平均自信息量。一个值域为{x1，…，xn}的随机变量X的熵H 定义为［1-2］

其中:E 代表了期望的函数;I(X)是X 的信息量(又称为信息本体)，I(X)本身是个随机变量。如果p 代表了X 的概率分布，则离散信源的信息熵公式可以表示为

如果p 代表了X 的概率密度函数，则连续信源的信息熵公式可以表示为

其中，b 是对数所使用的底，如上所述，通常是2、自然常数e或10。信息熵并不是负熵，它描述信源的不确定性，而不是不确定性的减少。信息熵大表示信源的不确定程度较大。

潜艇声探测传感器每隔一定时间对环境进行采样，这将增强作战系统对环境的认识，即减少目标信号的不确定性。信息论中，信息熵是信号不确定性的度量。潜艇声探测传感器采样前后信息不确定性减少的数量用信息增量描述［3-5］

其中:(x-)为先验概率;(x+)为后验概率。

为了说明信息增量在传感器多目标信息探测中的应用，首先考虑单个探测单元，并假设该探测单元内最多只能存在1 个目标。

用~s 表示单元的真实状态，~s =1 表示单元中没有目标，~s=2，…，S 表示单元中存在1 个目标类型。在先验信息的基础上，一个单元处于状态s 的概率由先验分布Q(s)给出。设P(s)是后验概率，表示基于某些量测，单元处于状态s 的估计概率。当P=Q 时，先验分布得出了最少的信息。由下面的概率表示了完备的信息:

假设对象集O 是一个无限集，其中每个元素下标取自于有限集s=0，…，S。从集合O 中随机抽取了n 个对象。先验概率Q［s］=qs给出了抽取一个由下标s 标识的对象的概率(Q 可以统一取qs=1/S)。随机抽取n 个对象，对象s 出现了ns次的概率由多项分布描述:

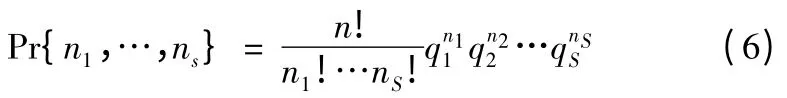
其中o(n)函数随n 次线性增长。

式(4)的意义:当分布P 很小，则I 扩大，并且相对于先验信息，后验信息P 具更大的信息量，在探测/分类问题中，后验估计与先验概率相差很悬殊的那些单元包含了大量的信息，相反，后验估计与先验概率相近的那些单元包含了少量的信息。对于目标信息探测来讲，从那些后验估计与先验概率接近的单元中只能获得相对较少的信息;对于那些具有较低识别值的单元，其后验信息P 具有大量的信息，所以期望的信息增量是最大的。

2 目标探测信息增量的计算

信息增量的大小可以反映一次探测所获得的目标信息的多少。为了计算多目标探测问题的信息增量，首先对探测环境建模:

将探测环境划分为C 个离散的单元c =1，…，C，每个单元的状态取自集合s=0，1，…，S，其中s=0 代表单元中不存在目标，s=1，2，…，S 代表单元中存在的目标类型，每个单元至多存在1 个目标。由1 个传感器探测这些环境单元，可以导引这个传感器使其探测任何一个环境单元，该传感器1 次只能监视1 个环境单元。对1 个单元探测完毕，传感器可以对同一单元或者任何其他单元进行探测。当传感器对一个单元进行探测时，该传感器会输出1 个离散的测量向量或测量集合z。这些观测输出是独立同分布的随机事件。单元c处于状态s 的条件下输出z 的条件概率Pc［z|s］已知，c 处于状态s 的先验概率Pc［s］已知。

综上所述，多目标探测问题就是基于一组观测集合，确定每个单元所处的状态。单元c 的第k 次观测输出为zk(k=1，2，…，K)，设ZK=(z1，…，zK)。总共观测了K 次，在K 次观测后，基于这些观测推算单元c 处于状态s 的后验概率为Pc［s|ZK］。对于每一个单元c，多目标探测的目标是通过选择s 获得最大的Pc［s|ZK］。

对于每个单元，使用贝叶斯公式计算K 次观测的条件下单元处于状态s 的概率。观测ZK的总概率是

因为集合ZK的数据是独立同分布的，所有

当前环境单元所处的状态的概率为

分母的累加形式中，t 描述了环境单元的状态。

K 次观测后，使用当前的P［s|ZK］计算信息熵:

传感器每次采样，都需要重新解算式(11)。但是，若式(10)可以用递归的方法计算，那么式(11)也可以用递归的方法计算，可以大大减少计算量。

将式(12)代入式(10)得

注意到对1 个单元进行K -1 次观测后，由于状态s 互斥且完备，所以第K 次观测的概率密度计算公式为

对单元c 进行探测、识别的信息增量为

基于识别的传感器管理策略就是选择使I 最大的单元c。其中K 是当前对单元c 的观测次数，对于不同的单元观测次数一般不同。

3 实例

首先，研究Bernouli 探测问题，单次观测的检测概率pd=0.8，单次观测的误警率pfa=0.5。观测系统中期望的目标数量为1。系统先验目标分布是一致的，所以每个单元中包含目标的概率为q=1/C。对于这样的问题，单元状态S=2，相对的概率和分布就容易评估。例如，如果一个单元包含目标的概率为pt，则使用式(10)计算信息熵

设对于一个包含目标的单元来讲检测出目标存在，这种情况的平均后验概率用式(12)计算是一个不包含目标的单元被检测出目标存在的平均后验概率。在导向查找的识别和导向查找(C=100 个单元、这些单元的状态取几次试验的平均结果的情况下进行的直接查找)之间进行比较。在导向查找的情况下，系统中的每个单元被连续地采样，并且对每个单元采用的次数相同。50 次试验、每个单元进行10次采样的结果:对于导向查找的识别对于导向查找比较上述2 个结果，使用识别-导向查找的概率估计的准确性潜在的提高了。

其次，使用阈值数据在白噪声背景下的高斯目标检测问题是较复杂的问题。当无目标出现时，期望的信号强度是N0;当目标出现时，期望的信号强度是S0+N0。对于这个问题优化的信号采用检测器是一个遵从Neyman-Person 阈值测试的诺斯过滤器。过滤器的输出λ 被阈值限制以产生一次量测的z，λ=1 代表阈值通过，λ≠1 代表阈值没通过。使用多次量测Zk，使用式(12)估计目标出现或未出现的概率。当没有目标出现时，λ 的方差为σ2=2S0/N0，分布为

当目标出现时，λ 的分布为

一次采样的误警率为

对于每一次单元采样，利用传感器对目标进行探测必须解决2 个问题:选择哪一个环境单元进行探测?阈值τ 为多大?可以选择τ 使每一次采样期望的信息增量I 最大。图1显示了信噪比是0 dB 时，目标位于某单元的估计概率pt取不同值时，I 随阈值τ 的变化。当pt=0.5 时，期望的信息增量最大，此时最优的阈值是τ*=/2。当pt≠0.5 时，最优阈值也不是/2。作为pt的函数，信息增量用于优化每个单元的阈值。但是，注意到，随着pt远离0.5，τ -独立性降低通过使用固定的阈值。

图1 信息增量随单元状态的变化曲线

4 结束语

本文提出了利用传感器进行多目标信息探测的一种方法，介绍了信息熵的概念和信息增量的计算方法。通过仿真实验说明了算法的正确性与实用性。

［1］吴湘淇.信号、系统与信号处理［M］.北京:电子工业出版社，1999:263-276.

［2］田宝玉.信息论基础［M］.北京:人民邮电出版社，2008.

［3］Keith K.Discrimination gain to optimize detection and classification.［J］. IEEE Transactions on SMC，1997，27(1):112-116.

［4］Stan M，Keith K.Comparison of sensor management strategies for detection and classification［M］.［S. l.］:International Symposium on Sensor Fusion，1996:128-137.

［5］刘先省，周林，杜晓玉.基于目标权重和信息增量的传感器管理方法［J］.电子学报，2005，33(9):1684-1687.

［6］李琪，郭娜，刘先省，等.基于Unscented 粒子滤波的传感器管理算法［J］.火力与指挥控制，2011(6):77-80.