基于地震波的弹丸落点定位模型
马朝军,狄长安,孔德仁,刘新爱,刘晓青
(南京理工大学 机械工程学院,南京 210094)
1 背景意义
在靶场试验中,经常需要确定弹丸的落点和回收弹丸,因而寻找弹落点位置就成为试验中的必要环节。对弹丸的落点测量,传统的方法是采用人工排查寻找弹丸,而在广阔的靶场,由于地形较复杂,人工排查不仅费时、费力,甚至有可能无法获取弹丸位置。声定位系统的探测范围小,只有当信号源进入探测区域时才能对其定位。GPS 接收机的响应时间相对较长,在需要高过载、高压力、高速、高旋的情况下,GPS 接收机的应用受到了挑战;同样,红外探测系统的探测范围小,且红外激光的方向性很强,对机动目标来说,该方法也不适合[1]。目前,靶场对于落点的测试设备有电视经纬仪、雷达等,利用这些设备,虽然精度较高,但其对低空及近地目标应用受到一定限制。利用弹丸落地地震波测量弹着点的方法与地震勘探的原理是一样的,炮弹落地会激起的地震动信号,用地震动传感器通过简单的布阵,就能实现弹着点的定位[2]。基于这种情况,为了能快速准确地确定弹落点的具体位置,本文提出了基于弹丸落地地震信号的弹着点定位方法。
2 定位原理
弹丸落地是一种冲击点源振动,弹丸落地瞬间,将产生很大的冲击力,使地介质的质点通过相互间的弹性作用力在自身平衡位置上震动,同时把震动状态传出去,形成地震波。远距离接收到的地震波主要有3 种:纵向压缩波(P 波)、横向压缩(S 波)和瑞雷波(R 波)。典型的弹丸落地产生的地震信号如图1 所示。

图1 典型的弹丸落地产生的地震信号
当地震信号到达时,最先到达的纵波由于能量小、速度快,会形成一个弱脉冲;随后由于横波和面波的速度相当,携带着绝大多数的能量,会形成一个强有力的脉冲地震动。
基于TDOA 的定位是根据不同的检波器接收到的地震信号时间的不同,由时间差推算到信号的路径差。当1 个目标到2 个地震检波器的距离差已知时,它对应的子集是以2个检波器为焦点的双曲线,利用三站就可形成2 条单边双曲线来产生交点,就能把弹丸的位置确定下来[3]。基于TDOA的定位方法的重点是解决传感器的布阵方法和如何提高时间测量精度的问题。不同的布阵方法得到的定位精度也不同,本文主要分析双三角8 点阵的布阵方法及误差。
3 布阵方法
3.1 双三角8 点阵的布阵方法及数学模型
如图2 所示,x 轴为测试区域下边缘,原点O 位于边缘的中心位置,y 轴垂直于x 轴。a 为等边三角形的边长,b 为检波器S1、S5基阵到坐标原点O 的距离。设弹着点的坐标为(x,y),各检波器的位置为Si(xi,yi),S4和S8放置在三角形的中心位置。
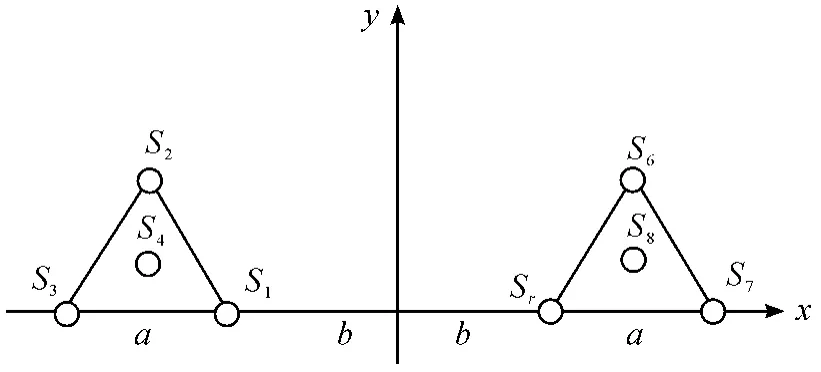
图2 双三角布阵图
当地震波以一定的速度v 到达各检波器时,由于存在距离差,使得信号到达各传感器存在时间差,利用两点间距离公式可以列出它的方程

式(1)中i,j =1,2,…,8。
理论上只要方程大于3,就可以通过公式求解出弹着点的坐标(x,y)。由于时间差是1 对检波器间的计算,对于检波器的选择有一定的限制。本文中尽量选择间距较大的2个检波器组建方程,分别将检波器1、2、3、4 对其他检波器配对列出方程组。
3.2 双三角8 点阵的模型仿真与误差分析
设弹着点测试区域为2 km×2 km,采取分区的方式进行仿真计算:
1)设x 轴向从-1000 m 到1000 m,每隔500 m 取值,沿y 轴从0 到2 000 m,每隔50 m 选点。
2)设y 轴向从0 到2 000 m,每隔500 m 取值,沿x 轴从-1000 m到1000 m,每隔50 m 选点。
3.3 双三角8 点阵的仿真计算
1)首先设a =5 m,分别取b 为800、900、1 200、1 500。当沿x 轴向增大时,其仿真结果见图3。
从图3 可以看出,当b 的取值较小时,在远离x 轴中心位置时,其误差比较大,随着x 值向坐标原点靠近而减小,而当b 值增大1 200 m 时,它在x 值处于任何值时,其误差都能满足测试要求。
沿y 轴向增大时,其仿真结果如图4。图4 表明,随着y值的增大,其误差呈现出逐步增大的趋势,随着b 值的增大其误差逐步减小,当b =1 200 m 时,其误差都小于2 m。综合考虑以上2 种情况,取b=1 200 m。
2)固定b=1 200 m,分别设a =5 m、10 m、20 m、50 m。当沿x 轴向增大时,其仿真结果如图5。
当沿y 轴向增大时,其仿真结果如图6。从图6 可以看出,a 的取值对整个系统的误差精度影响不大。取a =10 m能满足实际的需要。
最后以a=10 m,b=1 200 m 对整个测试区域进行仿真,分别沿x 轴向、y 轴向,主对角线、次对角线。其仿真结果如图7 所示。
从图中可以看出,沿y 轴向变化时,随着y 值的增大误差随之增大,在y=2 000 m 时误差最大,而沿x 轴向变化时,在中心位置误差最小,随着x 偏离中心误差增大,误差范围在2 m 以内,符合系统要求。

图3 a=5 m 改变b 值,x 轴向增大
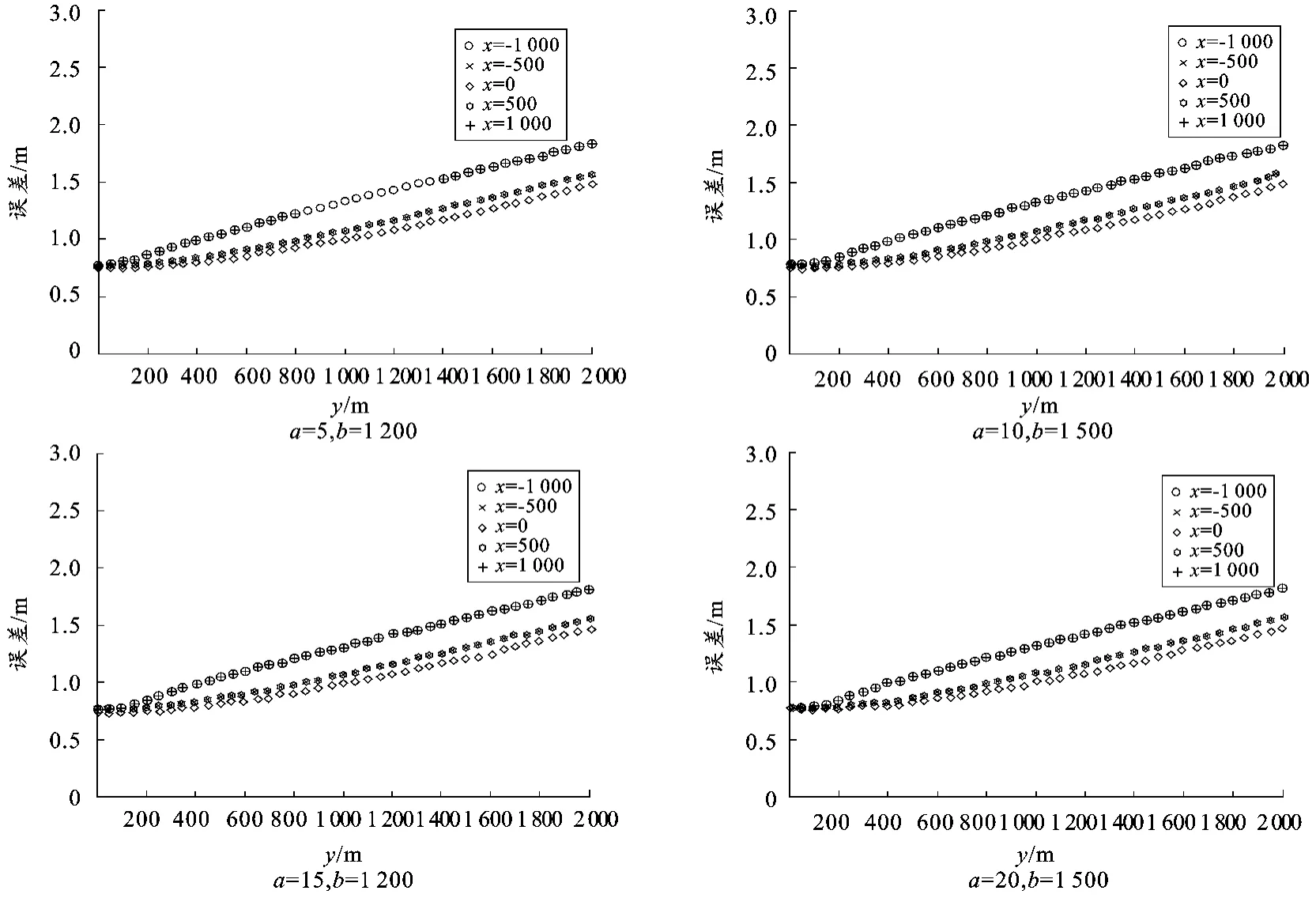
图4 a=5 m 改变b 值,y 轴向增大

图5 b=1 200 m 改变a 值,x 轴向增大

图6 b=1 200 m 改变a 值,y 轴向增大

图7 a=10 m,b=1 200 m 综合仿真
4 结束语
利用弹丸落地产生的地震波来对弹着点进行定位的关键技术是传感器阵列和精确地时延估计。仿真结果表明,双三角8 点阵在合理选择布阵参数的情况下,可以在2 km ×2 km范围内对弹丸落点进行定位,仿真的计算结果表明参数b 对定位精度的影响比较大,随着b 值增大,误差范围明显减小;而参数a 对误差的影响不大。最终确定参数a =10 m,b=1 200 m,其定位误差可达到2 m 以内。
[1]贾丽娜.基于相差测量原理的兵器实验弹落点的无线电定位方法的研究[D].太原:中北大学,2007.
[2]胡广新,赵向阳.基于弹头落地的地震波测量落点坐标[J].装备指挥技术学院学报,2006(2):116-120.
[3]蒋萍,狄长安. 基于声学立靶的传感器阵列模型研究[J].火炮发射与控制学报,2011(4):38-40.
[4]蒋东东,狄长安.基于被动声定位的大靶面弹着点坐标测量方法研究[D].南京:南京理工大学,2010.
[5]冯正.高速异常飞行体落点定位系统软件设计[D].太原:中北大学,2009.
[6]毕延文. 基于时差法的飞行器声被动定位技术研究[D].西安:西安电子科技大学,2005.
[7]季瑞.被动声探测系统及应用研究[D].西安:西北工业大学,2007.

