某型导弹发射装置伺服系统永磁同步电机建模与仿真
苏正波,赵修平,那晨旭
(1.海军航空工程学院 飞行器工程系,山东 烟台 264001;2.海军59193 部队,辽宁 大连 116041)
随着空袭武器性能的不断提高,对防空导弹武器系统的性能要求也越来越高[1]。对于采用倾斜发射方式的中近程防空导弹,其发射装置伺服系统的性能好坏对防空导弹武器的性能有很大影响。执行电机是伺服系统的动力装置,对于伺服系统的性能有至关重要的作用。
伺服系统常用的电机类型有永磁直流电机、交流永磁同步电机、异步伺服电机等。交流永磁同步电机(PMSM)具有体积小、质量轻、效率高、惯性低及转子无发热等优点,在伺服系统中得到广泛的应用。本文分析了永磁同步电机的数学模型,对矢量控制方法中id=0 的情况进行研究[2],在Matlab/Simulink 平台下建立该系统的仿真模型,并进行仿真。
1 永磁同步电机的数学模型
永磁同步电机具有复杂的结构,要对其建立数学模型,就要对其进行一定的合理假设。同时,为了简化及求解永磁同步电机的数学方程,通常使用电机坐标变换理论对永磁同步电机基于自然坐标的基本方程进行线性变化,实现电机数学模型的解耦[3]。
以三相静止abc 轴系表示的定子电压矢量方程为

将方程(1)进行Clark 变换和Park 变换,得到d-q 坐标系下PMSM 的定子电压方程为

d-q 轴的磁链方程为

电磁转矩矢量方程为

ψs、is以d-q 轴表示,有:

将式(5)和式(6)代入式(4),可得

进一步把式(3)代入式(7),可得
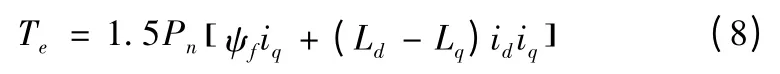
PMSM 的机械运动方程为
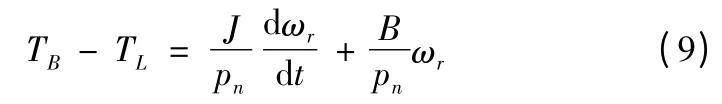
为了简化数学模型,这里可以设黏滞摩擦因数B =0。把以上方程进行整理,可以得到永磁同步电机的数学模型:

其中:ud、uq为d-q 轴定子电压;id、iq为d -q 轴定子电流;ψd、ψq为d-q 轴定子磁链;Ld、Lq为d -q 轴电感;Rs为定子电阻;pn为极对数;ωr为转子角速度;P 为微分符号;Te为电磁转矩;Tl为负载转矩;θr为转子电气角位移;θ 为电机转子机械角位移;J 为转动惯量;ψf为转子磁链;ψs为励磁绕组磁链;is为定子电流。
2 永磁同步电机的矢量控制原理
PMSM 矢量控制原理的基本思想是建立在坐标变换及电机的电磁转矩方程上,通过检测电机转子磁通的位置及幅值来控制定子电流或电压,电机的转矩只与磁通、电流有关,与直流电机类似,控制效果比较理想[4]。对PMSM 来说,转子磁通位置与转子机械位置相同,通过检测转子实际位置就可知道电机转子磁通位置。因此,矢量控制的实质就是控制定子电流空间矢量的相位和幅值。从前面的讨论可知,控制好id和iq便可以控制电机的转矩,一定的转速和转矩对应于一定的永磁同步电机可采用的电流矢量控制方法包括id=0 控制、最大转矩/流控制、弱磁控制以及最大输出功率控制[5]。本文采用的id=0 控制方案,当id=0 时,由式(7)可知,永磁同步电机的表达式为

该控制算法简单,电磁转子与定子的电流成正比,同时不会使永磁同步电机因退磁而导致性能变坏,并且易于实现。采用id=0 控制时实现了定子绕组与d 轴的完全解耦,通过控制iq就可以很好地控制电磁转矩,这和永磁直流电机的原理类似。本文设计的永磁同步电机控制就采用id=0 的矢量控制。图1 是某型导弹发射装置方位随动系统矢量控制原理。
从图1 中可以看出,这是一个由速度、电流反馈组成的双闭环系统,其控制过程为:速度指令信号与检测到的转子速度信号相比较,经速度控制器的调节,输出iq指令信号(电流控制器的给定信号);同时通过电流控制器使id=0,iq与速度控制器输出的iq相等,经过坐标变换将id、iq转换为定子三相电流ia、ib、ic;然后由PWM 模块输出6 路PWM 波驱动逆变器,产生可变频率和幅值的三相正弦电压驱动电机运转[6]。

图1 PMSM 矢量控制原理
3 Simulink 仿真模型
在Matlab7.0 的Simulink 环境下,利用Sim-PowerSystem丰富的模块库建立了永磁同步电动机矢量控制系统的仿真模型。该模型主要包括坐标变换模块、电流速度PI 调节模块、空间矢量脉宽调制模块(SVPWM)、逆变器和电机模型[7]。整体设计框图如图2 所示。
空间矢量脉宽调制模块内部结构如图3 所示。该模块着眼于使电动机获得幅值恒定的圆形磁场,以三相对称正弦电压供电时交流电机中的理想磁链圆为基准,通过逆变器不同的开关模式所产生的有效矢量来逼近基准圆,即用多边形来逼近圆形。由于逆变器产生的矢量数目有限,不能产生角度连续变化的空间矢量,只能通过8 个基本空间电压矢量中2 个相邻的有效矢量及零矢量,根据各自作用时间不同来等效电机所需的空间电压矢量。

图2 PMSM 矢量控制系统模型整体设计框图

图3 SVPWM 模块内部结构
4 仿真结果与分析
在对此闭环系统进行仿真前,需要对Simulink 仿真环境进行设置。仿真参数的选取算法为ode23t,可变步长,相对误差为0.001 s。本例仿真中用到的永磁同步电机参数:直流母线电压380 V;额定转速nN=2 000 r/min;额定转矩TN=6.8 N·m;极对数pn=4;定子d 轴绕组电感Ld=8.5 mH;q 轴绕组电感Lq=8.5 mH;定子绕组电阻Rs=2.875 Ω;转子的磁场磁通量φf=0.162Wb;转子的转动惯量J =0.008 kg·m2。系统在t=0 时空载启动,并且预设初始转速为500 r/min,启动给定转速为1000 r/min。在t=0.1 s 的时候加上20 N·m 阶跃干扰,可得到转速响应曲线、转矩响应曲线以及ia、ib、ic三相电流曲线。
从图4 可以看出,永磁同步电机的转速在0.02 s 内由初始的500 r/min 快速上升并经过0.005 s 的波动之后迅速达到稳定的1000 r/min;在t=0.1 s 时由于系统突加负载转矩20 N·m,电机转速经过0.007 s 的波动后达到稳定,电机转速基本没有波动,说明系统抗干扰能力强。

图4 电机转速响应曲线
由图5 可以看出,三相定子电流在电机转速发生变化时产生很大的波动,经过0.002 s 后电机转速稳定,三相电流重新达到震荡状态。在系统突加20 N·m 干扰负载时,三相电流经过短时间的波动达到给定的值,定子电流随负载变化而快速响应,并且迅速达到稳态,系统的动态性能良好。

图5 三相电流响应曲
由图6 可以看出,电磁转矩在电机开始变速时产生较大的波动,经过0.02 s 后达到稳定。在系统突加20 N·m 干扰负载时,电磁转矩经过片刻波动便达到稳定值,这说明电磁转矩反应很快,能够迅速跟踪负载转矩。

图6 电机转矩响应曲线
5 结束语
本文分析了PMSM 的数学模型及矢量控制原理,在Matlab/Simulink 环境下建立了永磁同步电机矢量控制系统的仿真模型。仿真结果显示:系统响应快速且平稳,转速和转矩超调量非常小,系统起动后保持恒定转矩;突加扰动时系统波动较小,充分说明系统具有较好的鲁棒性。本文采用的方法简单、准确可靠,对实际永磁同步电机伺服系统的数字化设计与实现提供了理论支撑。
[1]郝丕英.防空导弹发射装置伺服系统[M].北京:宇航出版社,1992:15-23.
[2]杨兴瑶.电动机调速的原理及系统[M].北京:水利电力出版社,1995:25-28.
[3]李永东.交流电机数字控制系统[M].北京:机械工业出版社,2002:24-35.
[4]Bin Zhang,Yaohua Li.A PMSM Sliding Mode Control System Based on Model R eference Adaptive Control[J].Power Electronics and Motion Control Conference,2000(1):336-341.
[5]辛小南,贺莉,王宏洲.永磁同步电动机交流伺服系统控制策略综述[J].微特电机,2010(2):67-70.
[6]Zhao L M.A DSP-based super high-speed PMSM optimization[C]//2004 IEEE 11th Digital Signal Workshop and 2nd IEEE Signal Processing Education Workshop.[S.l.]:IEEE,2004:187-190.
[7]洪乃刚.电力电子、电机控制系统的建模和仿真[M].北京:机械工业出版社,2010:196-209.
[8]张森,石航飞,陈志锦,等.基于DSP 的永磁同步电机的矢量控制[J].兵工自动化,2011(10):71-74.
[9]曹晓辉,史云珠.高性能永磁交流伺服系统研究[J].火力与指挥控制,2009(8):171-174.

