基于支持向量机的发动机性能衰退指标分类和预测

李冬，黄帅，曹明川(.海军航空工程学院，山东烟台6400；.海军驻常州地区航空军事代表室，江苏常州30)

基于支持向量机的发动机性能衰退指标分类和预测

李冬1，黄帅2，曹明川1
(1.海军航空工程学院，山东烟台264001；2.海军驻常州地区航空军事代表室，江苏常州213022)

基于支持向量机几何距离建立表征发动机性能衰退程度的指标，并基于相空间重构理论对该指标进行多步预测，表明回归支持向量机结果优于神经网络预测结果。利用主元分析、核主元分析方法对发动机性能特征量约简并提取其主元，得到核主元分析的分类效果更好。利用交叉验证的方法优化分类支持向量机和核函数中相关参数，给出发动机性能衰退指标曲线。通过建立统计量的方法分析发动机性能变化，确定性能变化关键点。所得结论对做好发动机维护保养工作，延长发动机使用寿命具有一定的指导意义。

支持向量回归；性能衰退指标；支持向量分类；预测；概率密度分布

1 引言

对发动机进行状态监控和故障诊断，及时准确地评估和预测发动机性能状况，发现性能衰退迹象及潜在故障隐患，这对推动视情维修、减小维修使用成本和提高飞行安全具有重要意义。实际中，可供测量的发动机参数有限，且这些参数大多反映发动机整机的性能状况，缺少部件的特性参数，这对开展部件方面的性能研究具有一定的难度。本文结合发动机模型，通过计算得到性能衰退前后部件的性能参数和表征整机性能衰退的数据，作为发动机性能变化研究的基础。由于性能变化是一个逐渐变化的过程，受自身、环境的双重影响，给性能衰退研究带来很大困难。支持向量机和构建残差统计量是研究数据变化较新且很有效的方法，本文应用此两种方法对发动机性能衰退指标分类和预测进行研究。

2 基于支持向量机几何距离的性能衰退指标的建立

基于支持向量机几何距离建立发动机性能衰退指标。在分类支持向量机中，特征空间内反映发动机性能特征的参数向量x，及到最优分类面H的距离d，可由式(1)计算[1]。

式中：w为分类面的权系数向量，b为偏置系数。

式(1)表明，在分界面表征性能衰退数据的一侧，离分类面距离越远的发动机性能特性参数，表示性能衰退越严重。

将d进行归一化处理，有-1≤d≤1，di＜0时，xi∈{正常}，di＞0时，xi∈{异常}。在此基础上采用下式衡量发动机性能衰退指标，且0≤d≤0.8。这样就将发动机性能特性量变成了性能衰退指标。

3 构造参数优化准则

在分类支持向量机中，对于两类分类问题，采用Fisher线性判别准则优化选取相关参数。对于两类训练样本集X，X={xi,yi}，xi∈Rd，yi∈{-1,1}，i=1,2,…,n。这两类数据的数学描述分别给定为：

Fisher准则考虑将数据映射到一维向量上，判别准则可描述为：

式中：|m1-m2|表示两类样本间的距离，越大越好；同时各类样本内部尽量密集，即类内离散度越小越好。在这种情况下，判别函数J(θ)取得最大值。采用式(6)确定分类时所用数据的形式(原始数据，主元分析所得数据，核主元分析所得数据)。

基于支持向量机几何距离概率统计构造核函数参数优化准则[1]。构造数据方差：

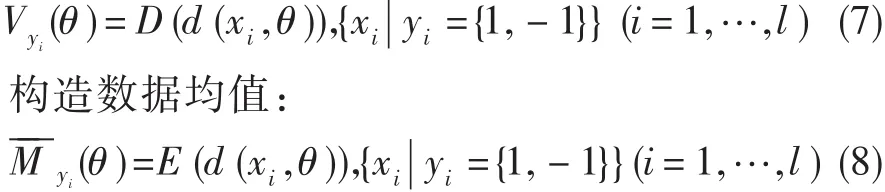
构造目标函数：

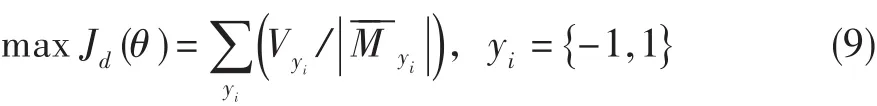
搜索Jd(θ)最大值，确定最优核函数相关参数θ。

4 相空间重构基础

采用回归支持向量机预测分析性能衰退指标。对于给定序列{x1,x2,…,xn}，建立映射关系f：Rm→R，满足：

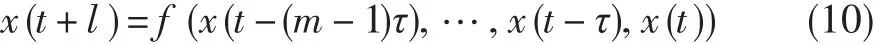
式中：l为预测步长，m为嵌入维数，τ为时间延迟。

对于上述时间序列，为了能采用回归支持向量机进行预测，首先应进行相空间重构，即将一维时间序列转化为矩阵形式获得数据间的关联，以挖掘尽可能大的信息量[2]，建立如下输入：

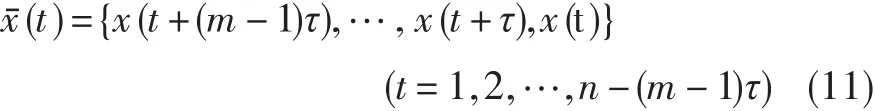
与输出y(t)=f{xˉ(t)}间的映射关系f：Rm→R。

从式(11)中可看出，m和τ值的优化选取，反映了利用最少且最有效的原始时间序列数据信息，最大限度地挖掘原始一维数据的时间序列信息。而对具体m和τ值的优化选取，尚无理论可借鉴，多采用反复试验和智能算法。m的最优选取说明了最大限度地挖掘原始数据序列中的相关信息；原始序列中的信息可能在几个时间点不变，但对未来性能衰退指标预测来讲，这几个点的贡献不大。τ的最优选取反映了以最少、最有效的数据信息进行预测，保证了所用数据进行预测的效率。

使用回归支持向量机对性能衰退指标进行预测分析。同时，为评价预测效果，引入下列评判标准：

绝对误差

式中：y(t)为真实值，yˆ(t)为预测值，n为样本大小。

5 交叉验证方案

在支持向量机分类和回归分析中，支持向量机中相关参数是影响分析精度的关键因素，因此有必要对其进行优化选择。本文采用交叉验证的思路，以优化两个参数(c1、c2)为例，具体步骤为：

(1)给定其最大值为c1,max和c2,max。

(2)使i=1:c1,max和j=1:c2,max变化，遍历所有的i和j。对于每一组i和j，对应着一组重构预测矩阵，利用其数据训练支持向量机，并记录此时的ik和jk(k∈[1,c1,maxc2,max])。

(3)采取打擂法，选取最小的i和j，记录此时最优的ibest和jbest。

(4)利用最优的ibest和jbest对未来测量参数时间序列进行预测，并对测量数据预测效果进行检验。

6 构造性能衰退指标统计量

利用回归支持向量机结合相空间重构理论，对发动机性能衰退指标进行预测。与实际值相减，得到性能衰退指标残差的时间序列。由于支持向量机方法的预测结果比较平稳，性能衰退点对应的残差变大，因此利用残差序列能较好地分析发动机性能状况。本文利用所求的性能参数指标残差序列构造统计量，完成发动机性能状况分析。

构建的基本思想[3]为：建立发动机性能衰退指标的残差序列ej(t)。当发动机工作在未知状况(健康或出现性能衰退)时，若性能处于健康状态，则残差方差在一定范围限制内；而发动机发生某种故障后，残差方差将显著增加。依据该属性，设计一统计量，用于检测发动机性能衰退程度。

(1)构造故障检测统计量。考虑当前时刻t，来自当前时刻(未知状况)、健康状况的残差方差分别为t)和(t)。利用q个向量计算当前时刻的方差估计量，并假定前几个样本方差在发动机健康状态下得到，利用初始q0个e(t)序列计算健康状态的样本方差。假定统计量F(t)=[t]服从F分布，则在不可信率α(置信水平1-α)下假设：

式中：Fu=F1-α(q-1,q0-1)服从F分布，如图1所示。

(2)构造故障分离统计量。下面测试所用序列e(t)，来自性能健康或不受考虑故障影响的发动机。设计q个样本的滑动窗口向量[e(t-(q-1)),…,e(t)]T在时刻t形成，构造如下统计量：

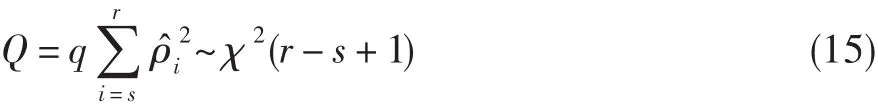
式中：s表示求和序号下限，通常取为1[4]；ρˆi为序列e(t)的自相关系数；Q统计量服从自由度为(r-s+1)的 χ2分布。

在不可信水平α(置信水平1-α)下，假设表述为：

式中：χ2(r-s+1)为服从(r-s+1)个自由度的χ2分布统计量，如图1所示(阴影部分为H0接受区域，空白部分为H1接受区域)。

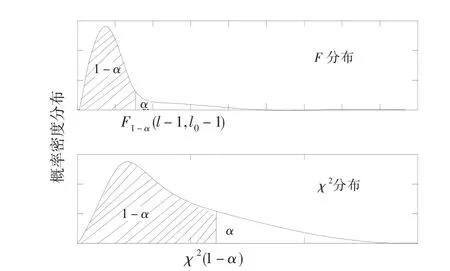
图1 统计量假设的概率密度分布函数Fig.1 Probability density function ofstatisticalhypothesis

7 仿真结果与分析

7.1 原始数据新主元的构建

首先，确定表征发动机性能的特征参数。本文取为{低压压气机流量，高压压气机流量，高压涡轮效率，低压涡轮效率，低压转子转速，高压转子转速，高压压气机后压力，尾喷口温度}，为八维数据，均为相对变化量[5]。其中，绝对值在0～0.2%变化的参数为性能正常数据(分类记为-1)，否则为性能衰退数据(分类记为+1)。其次，按前文方法将八维发动机性能特征量转化为一维数据，建立反映发动机性能变化的性能衰退指标。最后，采用支持向量机对发动机正常数据和性能衰退数据进行分类。三种形式的数据分别取为原始数据、原始数据利用主元分析[6]所得数据和原始数据经核主元分析[1]所得数据，对应的类内类间距离。计算结果见表1。

由表1可知，原始数据形式与主元分析所得类内类间距离相同，均比核主元分析的小。原因为主元分析是对原始数据进行线性变换，并不改变原始数据的类内类间距离；而核主元分析(高斯核函数)进行的是非线性变换。因此采用原始数据经核主元分析所得数据进行分类。

表1 三种数据形式对应的类内类间距离Table 1 Corresponding distance data ofinside classes and between classes

7.2 核函数的选取

采用原始数据经核主元分析所得数据进行分类。采用参数优化准则和交叉验证方案优化核函数相关参数，结果见表2。可见，高斯核函数对应的类内类间距离最大，因此采用高斯核函数进行分类。

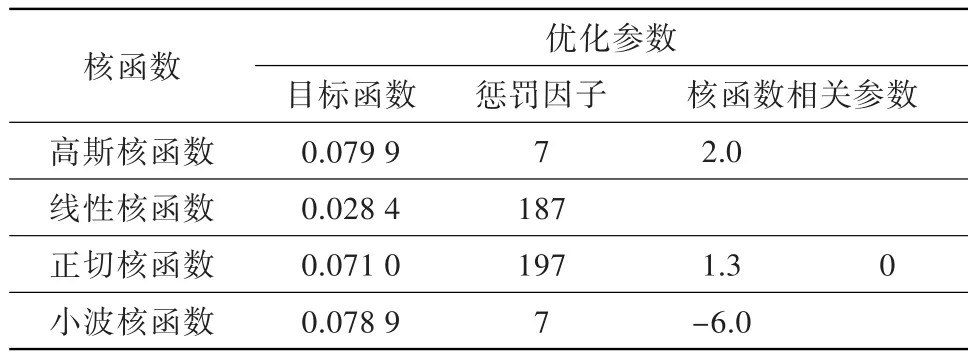
表2 核函数及其参数的选取Table 2 Selection ofkernelfunction and parameter

7.3 支持向量机分类

采用支持向量机方法对三种形式数据(经过标准化处理)进行分类。取前三个主元在二维和三维情况下进行分类，结果如图2～图4所示。其中，PC1，PC2，PC3为原始数据、主元分析所得数据和核主元分析所得数据的前三维数据。

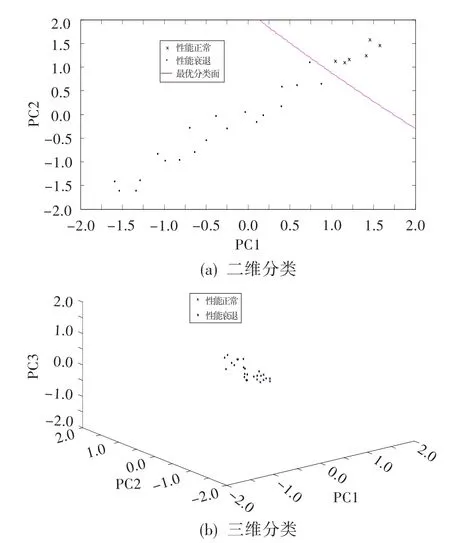
图2 原始数据分类结果Fig.2 Classification oforiginaldata

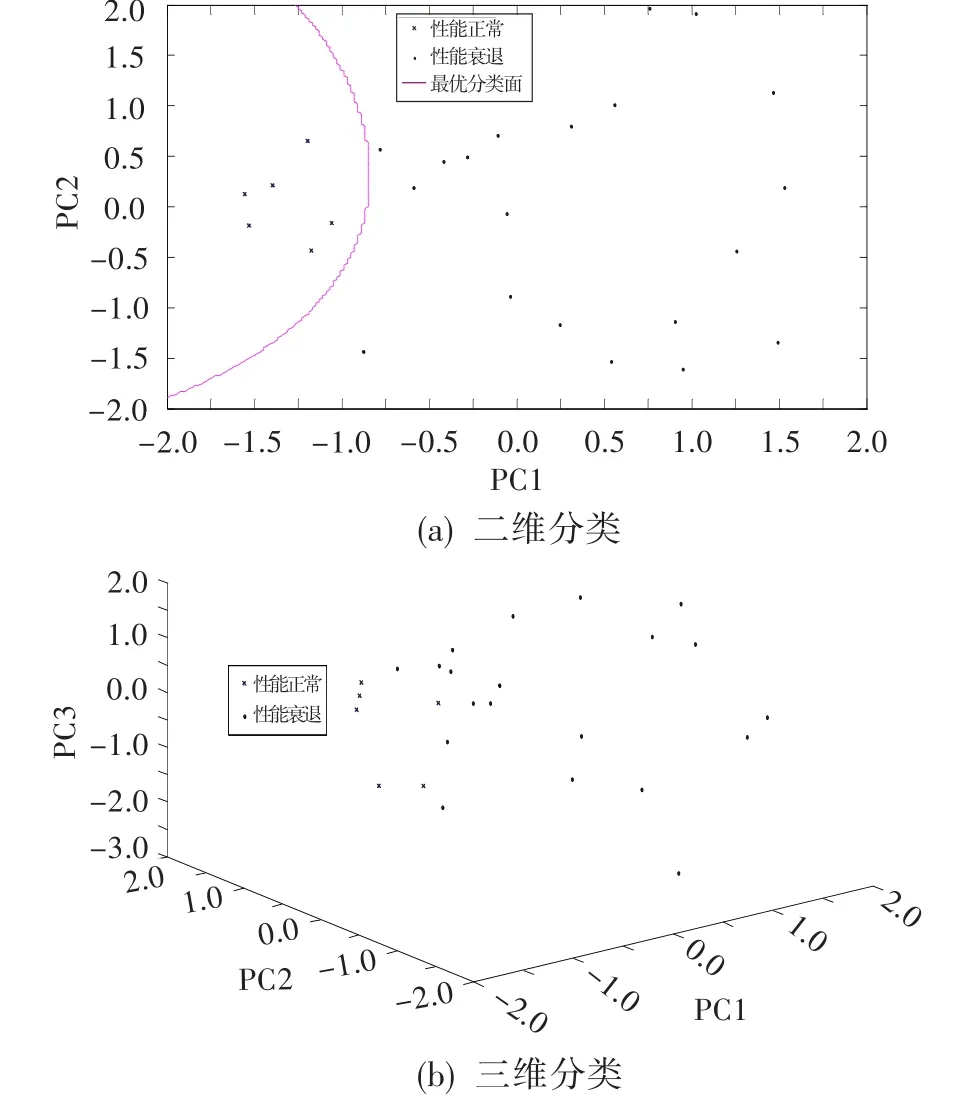
图3 主元分析所得数据分类结果Fig.3 Classification ofdata with PCA

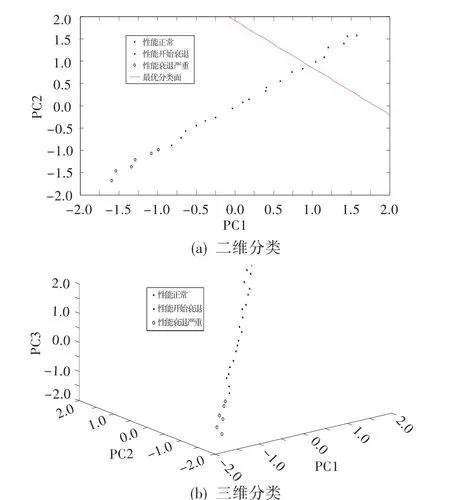
图4 核主元分析所得数据分类结果Fig.4 Classification ofdata with KPCA

由图中分析可知，二维分类情况下，三种数据形式都能得到很好分类；三维分类情况下，原始数据、主元分析所得数据得不到很好分类，而核主元分析所得数据仍能得到很好分类。原因为：二维情况下，两个主元的线性趋势较强，所以三种数据形式都能得到很好分类。三维情况下，三个主元的线性趋势变弱，非线性趋势增加，虽然采取了主元分析方法，但主元分析是一种线性变换，对非线性程度很强的性能衰退数据并不能得到很好分类；核主元分析则把低维的非线性不可分关系变成高维的线性可分关系，两个主元和三个主元情况都呈线性趋势，所以能得到很好分类。从图4中核主元分析情况看，性能衰退越严重，主元参数离最优分界面越远；三维分类中主元参数对应的衰退程度依次增大。因此，前文基于支持向量机几何距离建立的性能衰退指标合理。

7.4 性能衰退指标的报警阀值设置

按照自适应报警阀值算法[1]，所得报警阀值曲线如图5所示。图中的报警阀值计算，采取前几个点用于产生正常状态下的均值和标准差，不设报警限。设定n=10，即新进值连续10次超过数据的3倍标准差，才判断出现报警。每次输入14个指标并设置其报警限。第一级和第二级、第二级和第三级报警限之间均存在过渡地带，且出现超限报警。由于性能衰退指标是增函数，故只关注报警上限。

图5 性能衰退指标及报警阀值曲线Fig.5 Performance degradation index and alarm threshold curves

7.5 性能衰退指标的回归预测

采用相空间重构方法重构性能衰退指标数据。选择合适参数，利用回归支持向量机方法进行多步预测[7]，并与神经网络预测结果进行比较。其中，一步预测参数为惩罚因子C=1.3，不敏感损失系数ε= 0.001 2，核函数系数cof=1.1；两步预测参数为C= 1.3，ε=0.000 9，cof=1.1；三步预测参数为C=1.3，ε= 0.001 2，cof=1.1；四步预测参数为C=1.3，ε=0.001 0，cof=1.0。预测结果如图6、表3所示。采用式(13)作为评定预测性能的指标。

由图6、表3可知，支持向量机的预测精度高于神经网络，且随着预测步长的增加，两种方法的预测精度都下降。原因为预测步长越长，数据间的关联性越差，不确定度加大，预测误差变大。

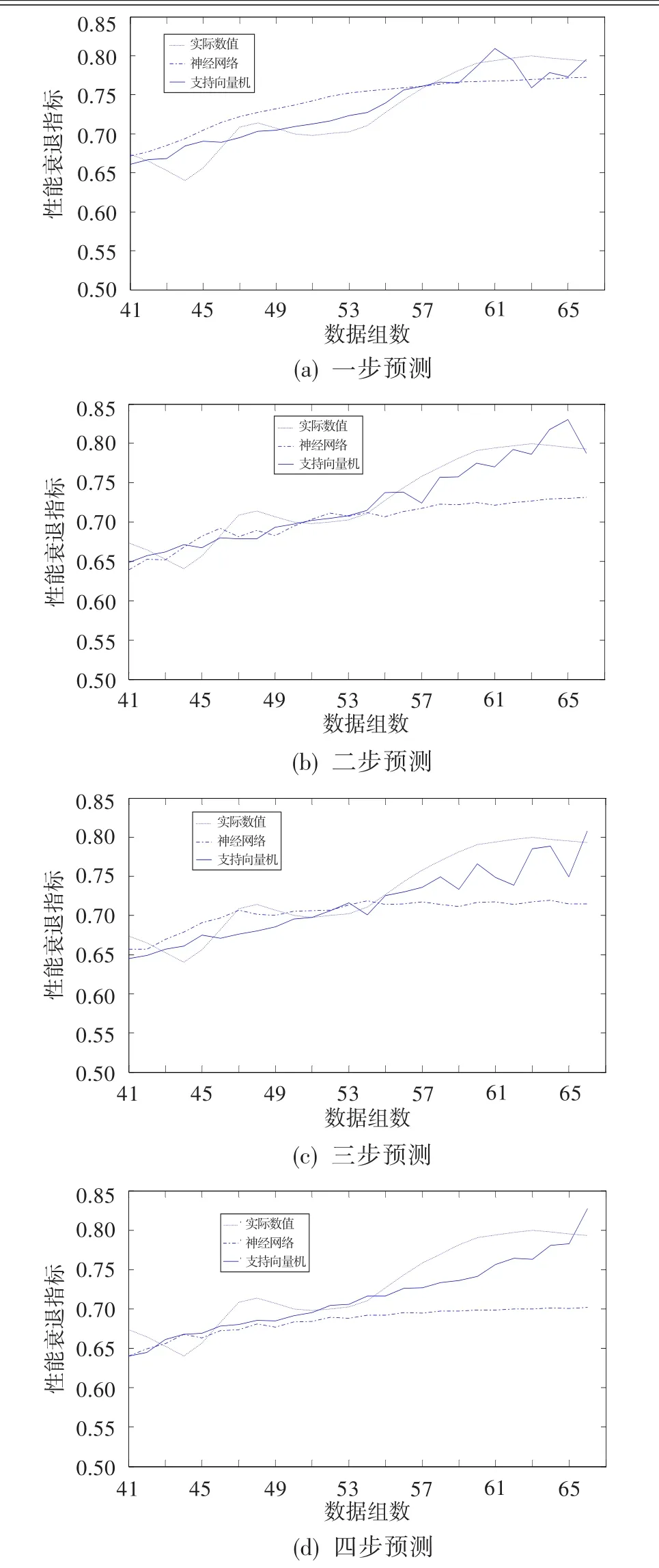
图6 多步预测结果Fig.6 Multi-step prediction results

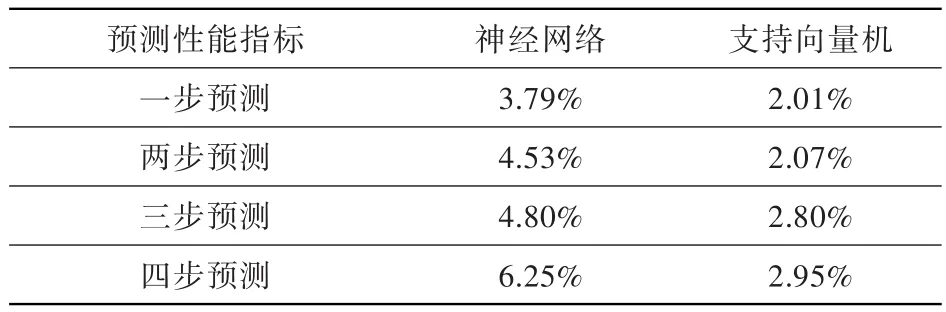
表3 预测误差对比Table 3 Comparison ofpredicted error

7.6 性能衰退指标的统计量分析

利用构造性能衰退指标的统计量，分析发动机性能状况变化，结果如图7和图8所示。图7表明，发动机未出现故障，但F统计量出现先减小后增加的趋势。在46点前性能变化平稳，之后性能出现衰退。而图8表明，发动机未受到考虑故障的影响，性能只是出现衰退，也未出现故障。

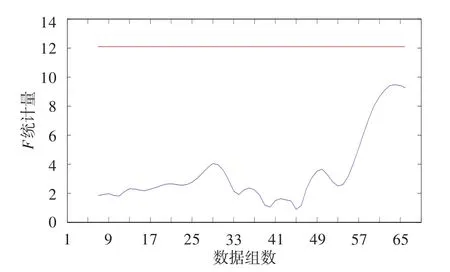
图7 性能衰退指标的F统计量Fig.7 F statistics ofperformance degradation index

图8 性能衰退指标的Q统计量Fig.8 Q statistics ofperformance degradation index

8 结论

本文基于几何距离建立表征发动机性能衰退程度的性能衰退指标，该指标能较好地反映发动机所处的性能状态。采用主元分析和核主元分析，较好地完成了对发动机性能衰退量的约简和分类。对性能衰退指标的多步预测表明，回归支持向量机预测精度比神经网络预测精度高。通过建立统计量的方法分析发动机性能变化，确定性能变化关键点，发现发动机目前的性能衰退程度均未超限。所得结论对做好发动机维护保养工作，延长发动机使用寿命具有一定的指导意义。

[1]郭磊.基于核模式分析方法的旋转机械性能退化评估技术研究[D].上海：上海交通大学，2009.

[2]胡金海，谢寿生，骆广琦，等.基于支持向量机方法的发动机性能趋势预测[J].推进技术，2005，26(3)：260―264.

[3]Dimogianopoulos D,Hios J,Fassois S.Aircraft Engine Health Management via Stochastic Modeling of Flight Da⁃ta Interrelations[J].Aerospace Science and Technology，2011:1―12.

[4]Söderström T，Stoica P.System Identification[M].London：Prentice Hall，1989.

[5]尹大伟.某型发动机模型修正研究[D].山东烟台：海军航空工程学院，2007.

[6]马逢时，何良材，余明书，等.应用概率统计[M].北京：高等教育出版社，1989.

[7]冯广斌，吴震宇，袁惠群.基于混沌理论与SVM的内燃机振动信号趋势预测[J].振动、测试与诊断，2011，31 (1)：64―69.

Classification and Prediction of Engine Performance Degradation Index Based on SVM

LIDong1，HUANG Shuai2，CAO Ming-chuan1
(1.NavalAeronauticaland AstronauticalUniversity，Yantai264001，China；2.Aeronautical Military Representative Office ofNavy in Changzhou Area，Changzhou 213022，China)

The engine performance degradation index was established based on geometricaldistance ofsup⁃port vector machine(SVM)and predicted by multi-step method based on phase space reconstruction theo⁃ry.The result of support vector regression(SVR)is superior to neural network.Performance characteristic parameters were simplified by principal component analysis(PCA)and kernel PCA(KPCA).The principal component was extracted and classification of KPCA was better.Parameters of support vector classification (SVC)and kernel function were optimized by cross validation.Curve ofengine performance degradation in⁃dex was presented.Variation ofengine performance was analyzed by establishing statistics to determine the key pointofperformance variation.The results provide reference forengine maintenance and life extension.

SVR；performance degradation index；SVC；prediction；possibility density distribution

V235.13

A

1672-2620(2012)03-0020-06

2011-07-23；

2012-06-28

李冬(1984-)，男，辽宁葫芦岛人，博士研究生，从事航空发动机性能衰退及评估预测技术研究。