我国国际储备资产的最优结构研究——基于时变Copula及VaR的投资组合模型分析

杨 楠，邱丽颖

（上海财经大学 统计与管理学院，上海200433）

一、引言与文献回顾

自20世纪70年代以来，黄金在国际储备中的地位被主权货币所取代。但近年美元汇率大幅下挫，黄金价格持续高涨，以美元为主要储备形式的国家面临严重的资产缩水，提高黄金储备规模引起了广泛关注。对于我国而言，2011年5月国际储备①已达232 020.69亿元人民币，其中96.37%为外汇储备，而美元占据70%。与同一时点上美国、德国、法国和意大利的黄金储备占其国际储备的比例分别达到78.9%、71.5%、72.6%和66.5%相比，我国持有的1 054吨黄金储备只占国际储备资产的1.6%，在美元下跌、金价上涨的形势下，国际储备资产价值损失严重，现有结构亟待调整。

国际储备资产管理是中央银行宏观经济管理的重要内容，其结构体系是否合理关系到一国的金融稳定，由此备受各国政府和国际金融组织的普遍重视。对于该结构体系的研究，西方理论界比较有代表性的模型有Markowitz（1952）的资产组合模型、Heller和 Knight（1978）模型以及Dooly（1981）模型等。其中，资产组合理论强调资产收益与风险在安排储备资产结构中的作用，更受到广泛的重视与研究应用。但是目前将其应用于讨论外汇币种结构的较多见，研究包含黄金在内的储备资产的最优结构还不多见。由于黄金兼具货币与商品双重属性，它与外汇之间的相关关系比外汇不同币种间的相关关系要复杂，刻画起来更有难度，对此还需要深入分析。近年关于黄金储备的价值和占比问题，国内外学者的研究主要围绕如下论题展开：黄金是否具有稳定的保值增值功能？黄金在一国的国际储备资产中应占据多少比例？

学者们普遍认为，黄金可以作为一种有效资产加入投资组合以实现保值增值。如Colin（2003）发现黄金的投资收益率与主要的宏观经济变量不具有显著相关性，从而可以作为有效资产来多元化投资组合。Forrest、Terence和Geoffrey（2004）通过探讨黄金与美元对日元、英镑、马克和法郎汇率变动的关系，证明了黄金是良好的抵御货币贬值风险的对冲工具。Rhona（2007）对比了21种期货商品在2005－2007年间的表现，发现黄金是最具信赖度的商品。

对于黄金在国际储备资产中的理想规模与占比，学者做了大量研究。David和Wainwright等（2005）通过对比贵金属与抗通胀债券发现，用黄金来衡量和对冲通胀风险的效果更佳，并建议投资组合由18%的黄金和82%的债券组成。Natalle（2009）认为中国、印度等新兴市场国家的黄金储备过低，若亚洲央行通过出售外汇增加1%的黄金储备，则需购买1 000吨左右的黄金。赵志良（2006）建立了黄金储备适度规模测算模型，计算得出中国目前较为合理的黄金储备总量应在3 000吨以上。张旭（2006）以全球黄金储备总量排名前十国家的数据为基础，利用回归模型分析得出黄金储备占外汇储备较为合适的水平为40%－50%。

无论是经济繁荣期还是衰退期，黄金都显示出价值上的持久耐力。周洁卿（2007）、刘辰君（2009）和周中明（2011）的研究都认为当前我国应增加黄金储备，但是黄金占比应提高多少，目前并没有一个基于理论与数据分析的明确结论。本文认为，随着国际金融市场冲击力量的出现和各国央行宏观经济政策的不断调整，国际储备资产的风险相关结构动态性逐渐增强，黄金的双重属性使它与外汇资产间具有更为复杂的相关关系，现有方法在准确刻画这种动态关系演变上仍有局限。基于此，本文设计使用时变Copula方法来加以解决，该方法能有效捕捉风险相关性的非线性动态特征，在刻画风险之间的相关性、联动性和传染性并测量集成风险方面有着广泛的前景。本文基于时变Copula计算组合资产VaR值，建立国际储备的结构优化模型，通过外生参数和效用函数形式讨论确定我国国际储备的最优结构。

二、基于时变Copula及VaR的最优投资组合模型设计

（一）研究设计

国际储备由外汇、黄金、IMF头寸（GDR）及特别提款权（SDR）组成。从世界范围看，GDR和SDR约占3%，而由于国际货币制度的约束，GDR很难自主增加，SDR作为账面资产虽然可以通过清算在成员国家间划转，但总量有限且交易不活跃。因而，本文以我国当前国际储备中最主要的两种资产——黄金和美元作为构建投资组合的要素，从收益与风险两个维度构建资产评估变量和效用函数，并求解使效用最大化的黄金占比。由于两者的收益、风险以及相关关系均可能随时间变化，本文采用时变Copula－GARCH模型，即利用GARCH模型估计单个资产收益率的边缘分布及VaR值，选取适当的Copula函数来描述两种资产之间的动态相依关系，利用Monte Carlo模拟计算组合资产的VaR值，代入效用函数，最终求得黄金最优占比。

（二）评估变量选择与效用函数构建

本文以累积回报现值和累积最大损失值来分别衡量收益与风险。对于i＝1，2且t＝1，2，…，T，令ri，t表示t时刻资产i的对数收益率，Ci和Li分别表示资产i的累积回报现值和累积最大损失值，定义如下：

其中，R为贴现率，本文使用一年期美元存款利率，VaRi，t为在一定置信水平下资产i在t时刻的最大损失，示性函数为：

基于回报现值C和最大损失值L，构造如下柯布－道格拉斯型效用函数：

其中，λ为外生参数，表示U对C的弹性；－（1－λ）为U对L的弹性，含义为最大损失值增加1%，效用减少（1－λ）%。

（三）动态相关性的Copula刻画与参数估计

本文使用Copula函数（Sklar，1959；Nelsen，1998）将二元资产的分布函数与其边缘分布连接起来。为了捕捉到当极值事件发生时尾部相关性可能增强的特征，我们使用T－Copula进行分析，其分布函数和密度函数分别为：

在估计（5）式和（6）式中的参数时，本文使用边缘推断法（IFM），②分两步进行：

第一步，用极大似然法估计边缘分布Fn（·）的参数vn（n＝1，2）：

第二步，估计Copula函数的参数α：

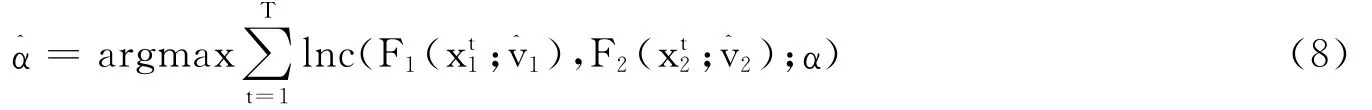
（四）时变Copula模型与VaR计算

本文通过给出Copula函数相关系数的演化方程来刻画变量间的动态相关关系。Patton（2001）最早根据Hansen（1994）自回归条件分布模型的思想，对正态Copula的相关参数给出过估计，并于2006年提出对称Joe－Copula模型等。Goorbergh、Genest和Werker（2003）提出由秩相关系数的演化过程来确定演化方程，Bartram、Taylor和Wang（2007）采用包含自相关和历史项之差的绝对值的演化方程。Dean（2006）把时变Copula和VaR结合，运用Monte Carlo方法，估计由SP500、Dax和Nikkei225等组成的投资组合的VaR值。本文结合Dean（2006）和Patton（2006）提出的模型，假定T－Copula自由度不变，建立用于估计二元序列的时变T－Copula函数参数的演进方程：

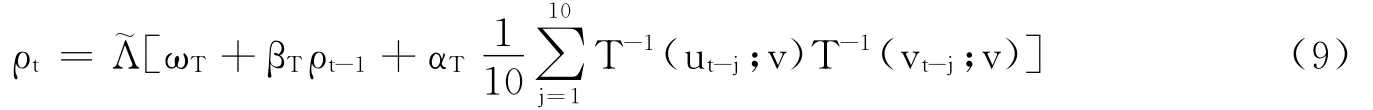
其中，ωT、βT和αT为待估参数，T－1（·；v）是自由度为v的T分布函数的逆函数，为修正的logistic函数。

对于组合资产，假定随机变量x和y分别代表两种资产的损益，边缘分布分别为F（x）和G（y），具有Copula函数C（F（x），G（y）），则投资组合超过一定阈值r的概率及相应的风险测度VaR（韦艳华和张世英，2008）为：

其中，w代表x在投资组合中的权重，r为阈值，与置信度1－α一一对应。P｛wx＋（1－w）y≤VaRα｝＝1－α，其中VaRα表示1－α置信度下的VaR值。

三、实证分析

（一）数据说明与探索性分析

本文选取2001年1月3日至2011年5月3日间的美元指数（Nominal Major Currencies Dollar Index）和黄金价格（London PM fix）的周数据，③数据来源于美联储网站与世界黄金协会网站。记美元指数为DIt，黄金价格为GPt，取对数收益率为分析对象。计算使用R语言实现。

经描述性统计分析，Ln（DIt）和Ln（GPt）的峰度分别为5.78和5.03，偏度分别为－0.15和－0.46，表明二者均具有尖峰厚尾和左偏形态。二者的JB统计值分别为172.45和109.54，均大于临界值，说明两序列都不服从正态分布。采用ADF检验对Ln（DIt）和Ln（GPt）的平稳性进行探讨，结果表明两序列均是平稳的。计算滞后15阶的自相关函数与偏自相关函数，结合比较AIC与SC准则，最终确定Ln（DIt）的均值方程为 ARMA（1，1），Ln（GPt）的均值方程为样本均值加一个随机扰动项。对均值方程拟合后的残差进行ARCHLM检验，结果显示两收益率序列的F统计值和LM统计值的p值都为0，表明存在显著的异方差效应，故可利用GARCH族模型来拟合数据。

（二）边缘分布模型的参数估计与单个资产VaR值

对｛Ln（DIt）｝Tt＝1和｛Ln（GPt）｝Tt＝1两列数据分别在正态分布和t分布假设下进行数据的模型拟合。实际应用中只用到低阶的GARCH族模型。本文取GARCH（1，1）对数据进行拟合。参数估计结果见表1。

表1 边缘分布模型的参数估计和检验

这里K－S检验的零假设为“变换后的序列服从（0，1）均匀分布”，表中K－S统计值及其概率值表明对各序列均无法拒绝零假设，④说明以上模型都可以较好地描述美元指数和黄金价格的条件边缘分布。K－S统计值的概率值越高，样本对模型的接受概率越高。对比正态分布和t分布假设下的K－S概率值可以发现，GARCH（1，1）－t模型对美元指数和黄金价格的拟合效果优于GARCH（1，1）－n，与之前的正态性检验结果相对应，即收益率具有尖峰厚尾的特征，正态分布的假定并不适用。因此，选择GARCH（1，1）－t作为边缘分布模型。

在对美元和黄金收益率数据分别进行拟合后得到标准化残差序列，进行ARCH－LM检验，F统计值和LM统计值的p值都很大，说明已不存在异方差效应，模型拟合效果非常好。根据模型使用收益率序列条件均值与条件方差的1步向前预测值，求解t分布的相应分位数点，分别得到两序列在t时刻的VaR值，对此VaR序列进行Kupiec检验，结果表明预测效果较好。

（三）时变Copula模型参数估计结果及组合资产的VaR值

1.Copula模型参数估计结果。基于（9）式来描述二元T－Copula函数时变的相关系数ρt，使用Patton（2006）的算法进行估计，结果见表2，对数似然值为－97.6856。其动态演化过程见图1，可以看到，2007年次贷危机后美元指数与黄金价格之间的负相关性达到最大，说明黄金在危机爆发时是非常有效的避险资产，因此对二者进行资产组合非常必要。

表2 时变Copula模型参数估计

图1 T-Copula时变相关系数动态演化

2.组合资产的VaR计算。组合资产VaR的解析式很难求出，本文借鉴Dean（2006）的方法，通过Monte Carlo模拟得到相应的分位点，主要步骤为：

（1）考虑包含两种资产x和y的投资组合z在t－1时刻的收益：

其中，xt－1和yt－1分别表示两种资产在t－1时刻的收益，w表示x的权重。

（2）对每种资产在［t－1，t］内做500次 Monte Carlo模拟，模拟服从Ct（·）的一个随机向量（uj，x，uj，y）′，此处产生二维时变 T－Copula的随机变量。⑤

（3）采用T分布，通过边缘分布的逆函数得到资产对数收益率的残差序列有：

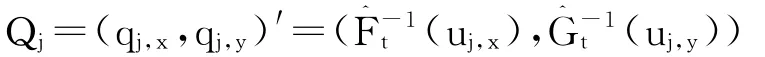
（4）通过GARCH模型中预测的方差和均值，得到两资产的收益率序列：

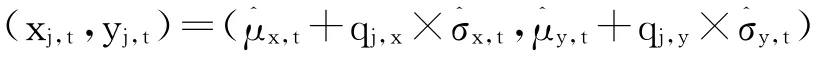
（5）重复以上过程j＝500次，重新计算投资组合在t时刻的收益：

（6）根据分位数即可得到95%水平下的VaRt。

根据估计出的时变相关系数和以上算法，对不同的资产权重w分别进行500次Monte Carlo模拟，设定w初始值为0.01，精度也为0.01，从而可以得到不同资产权重下组合资产在95%置信水平下的VaR值。图2是黄金占比w为20%时组合资产的VaR值序列：VaR序列恰好托住组合资产序列的下缘，且将穿透总次数代入Kupiec检验证实了预测效果较有效。重复同样步骤，考察其他黄金权重，如50%、80%等，也取得了较有效的结果。

图2 黄金占比w为20%时组合资产的VaR值

（四）黄金储备的最优占比

1.单个资产的收益与风险。根据（1）式和（2）式计算得到黄金的回报现值为0.8503，最大损失值为10.2437，美元回报现值为－0.2026，最大损失值为5.0445，说明黄金的收益高于美元，但美元的风险低于黄金。因此，构建资产组合是可行的。

2.资产组合最优比例。通过以下步骤进行：（1）设定外生参数λ。不失一般性，设λ＝0.3。（2）设定w1的初始值。本文取为0.01，可得到组合资产的收益率rz，t和在险价值VaRz，t。（3）将rz，t与VaRz，t分别代入（1）式和（2）式，可得组合资产的回报现值与最大损失值，再根据式（4）得到w1＝1%时的效用值。（4）设定w1的计算精度，这里使用0.01。在［0，1］范围内不断调整w1值，找到使效用函数U达到最大的w1，即黄金的最优占比，记为w＊1，对应的组合为最优资产组合。

计算求出黄金的最优占比w＊1为0.55，对应最大效用值为0.1965，即黄金应在国际储备资产中占55%（见图3）。此时，最优组合资产的回报现值为0.3672，最大损失值为6.9870。对比单个资产的收益与风险，可以看到最优资产组合的回报现值和最大损失值都介于之间，从而起到了降低风险的作用。

（五）外生参数和效用函数形式的讨论

图3 当λ＝0.3不断调整w1时效用的变化

1.外生参数λ的讨论。模型中λ是组合资产的效用U对回报现值C的弹性，即回报现值增加1%，效用增加λ%。在不同的λ下计算组合资产中黄金的最优占比，在一定精度下（本文取0.01）可以得到二者的一一对应关系（见表3）。当λ＞0.5时，λ／（1－λ）＞1，即为了增加1%的回报现值，需要计提的最大损失风险准备大于其自身持有资产，此风险偏好与实际不相符，因此只考虑λ≤0.5的情况。随着λ的增大，w＊1不断增大。也即，效用对于回报现值的弹性越大，需要计提的风险准备越大，黄金所占的比例应越高。w＊1最小为0.23，即在任何合理的风险偏好下，黄金的比例至少应为23%。

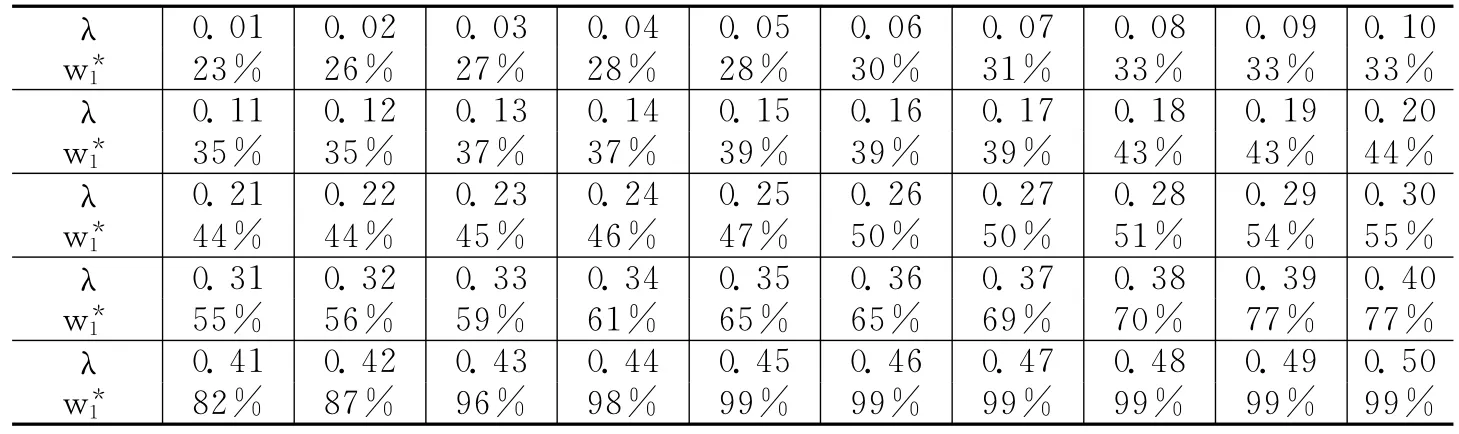
表3 不同的外生参数λ下组合资产中黄金的最优占比

2.效用函数形式的讨论。不同的经济学模型假设可以构造不同形式的效用函数。投资者对于风险有偏好、中立和厌恶三种取向，而风险偏好型不符合各国央行对于国际储备资产管理的原则。因而，除了上文的风险厌恶型的柯布—道格拉斯效用函数外，这里再讨论风险中立型的简单线性效用函数。该效用函数假设回报现值与最大损失值之间有稳定的伴生关系，形式为：

该效用函数对回报现值和最大损失值的弹性分别为λ和－（1－λ），这与柯布—道格拉斯效用函数相同。重复上面求解最优占比的4个步骤，求出基于线性效用函数的最优黄金占比。当外生参数λ＝0.3时，可求得最优比例为24%，即黄金在国际储备中的最优比例为24%。最优组合资产的回报现值C为0.0382，最大损失值L为5.0816，也都介于黄金和美元之间（此时黄金和美元的回报现值分别为0.8503和0.0383，最大损失值分别为10.2437和5.0445），起到了很好的降低风险作用。

同样，不断调整外生参数λ，只考虑λ≤0.5的情况，计算组合资产中黄金的最优占比，结果见表4。在线性效用函数下，λ从0.01逐渐增加到0.5，w＊1始终保持在22%－25%之间，而中国目前的1.6%远低于这个范围。

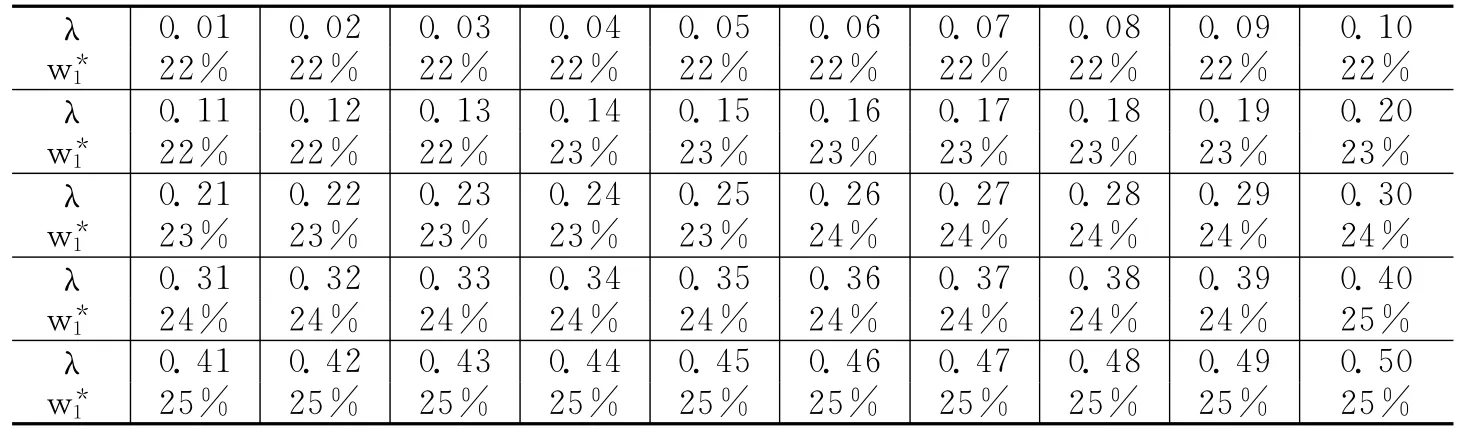
表4 线性效用函数不同的外生参数λ下组合资产中黄金的最优占比

对比两种效用函数可以看出，无论是基于非线性效用函数还是线性效用函数，求得的最优黄金占比都远高于中国目前国际储备中的黄金占比。因而得出结论——从保证国际储备资产收益和降低国际储备资产损失风险的角度来说，中国国际储备中黄金占比应在23%以上。若要达到此占比，则黄金与外汇储备均需要适时进行动态调整。在当前国内外复杂形势下，应秉持适时适度原则，逐步削减超额外汇储备，小规模稳步增持黄金储备。

四、不同类型国家黄金储备的收益与风险分析

（一）收益与风险的特征与动态趋势分析

在目前世界上官方黄金储备绝对量排名前20位的国家和组织中，本文按照黄金储备占比的不同选取14个代表性国家，从持有黄金储备的收益与风险角度进行静态分析（见图4），计算各国从2001年年初至2011年5月的回报现值C与最大损失值L，将这些点绘制在一张二维图上（以C＝0和L＝4进行象限划分）。可以发现：位于第I象限的美国、法国、德国、意大利和奥地利有高收益、高风险的特征，其持有黄金储备的比例很高，都大于50%；位于第II象限的印度、俄罗斯、中国和巴西有低收益、高风险的特征，其黄金储备占比都非常低，小于5%；第III象限对应于低风险、低收益的保守投资保值特征，样本国家中没有位于该象限的；位于第IV象限的比利时、瑞士、委内瑞拉、欧洲央行和英国有较高的收益、较低的风险，其所持黄金储备占比较高，基本在15%－50%之间。

在Ⅰ、Ⅱ和Ⅳ象限中分别选取两个代表性国家，基于（1）式和（2）式，以每年年末作为期末点Ti（i＝1，2，…，10），分别计算六个国家或地区从2001年年初至每个期末点Ti的回报现值Ci，j和最大损失值Li，j（下标j表示国家），并连结绘制成走势图（见图5）。可以发现，黄金占比不同，收益与风险的变化趋势显著不同。黄金占比很高的国家（美国和德国）向着收益和风险都逐渐增大的方向迅速发展，而且收益与风险基本同比例增加；黄金占比适中的国家或地区（欧洲央行和英国）风险在逐渐增大，但增速与美国和德国相比要缓和一些，收益则有一个回转趋势，即从正收益减小至负收益后又逐渐向正收益方向增大；黄金占比很低的国家（印度和中国）收益在逐渐减小，但风险却在逐渐增大。相比而言，黄金占比很低的国家（印度和中国）属于最糟糕的情况。

图4 各国回报现值和最大损失值静态比较

图5 黄金占比影响收益与风险的动态阐释

（二）黄金储备占比的分类分析

将黄金储备占比与各国收益和风险的动态变化进行总结（见表5）。可以发现：首先，发达国家的黄金储备所占比重远远高于发展中国家，发达国家的国际储备构成相对偏重于黄金，而发展中国家的国际储备构成则相对偏重于外汇；其次，黄金储备的占比范围对收益与风险的变化趋势有直接影响：

（1）第a类国家，黄金占比在50%－80%之间，大多为早期即持有大量黄金储备的发达国家，且在亚洲金融危机后大多有增持行为，如德国、法国和意大利分别增持黄金841吨、637吨和519吨。这些国家的中央银行注重通过有效的货币政策实现各项宏观经济目标，而且其国民收入已达较高水平，借助储备资产的结构管理获取收益的动机并不强烈，其最为看重的是储备资产的安全性。

（2）第b类国家，黄金占比在15%－50%之间，大多为早期持有大量黄金储备，但近年有减持的国家。它们大多为顺应黄金非货币化的历史潮流，抛出不可生息的黄金，换取可生息的外汇资产，增强其储备资产的盈利性和流动性。但是其减持黄金仅仅是调整储备结构，并非否认黄金作为国际储备资产和部分国际货币的性质。尤其欧洲联盟规定其成员国黄金储备应占总储备的15%，即使这些国家出售多余的黄金储备，其占比也不会低于15%。

（3）第c类国家，黄金占比非常低，在5%以下，为以金砖四国为代表的新兴发展中国家。由于国民收入较低，更为看重持有外汇储备的生息。另外，发展中国家的低收入使其无力保持较高的国际储备水平，而且对国际储备的流动性有更高的要求，所以还普遍具有较低的黄金储备和较高的外汇储备。

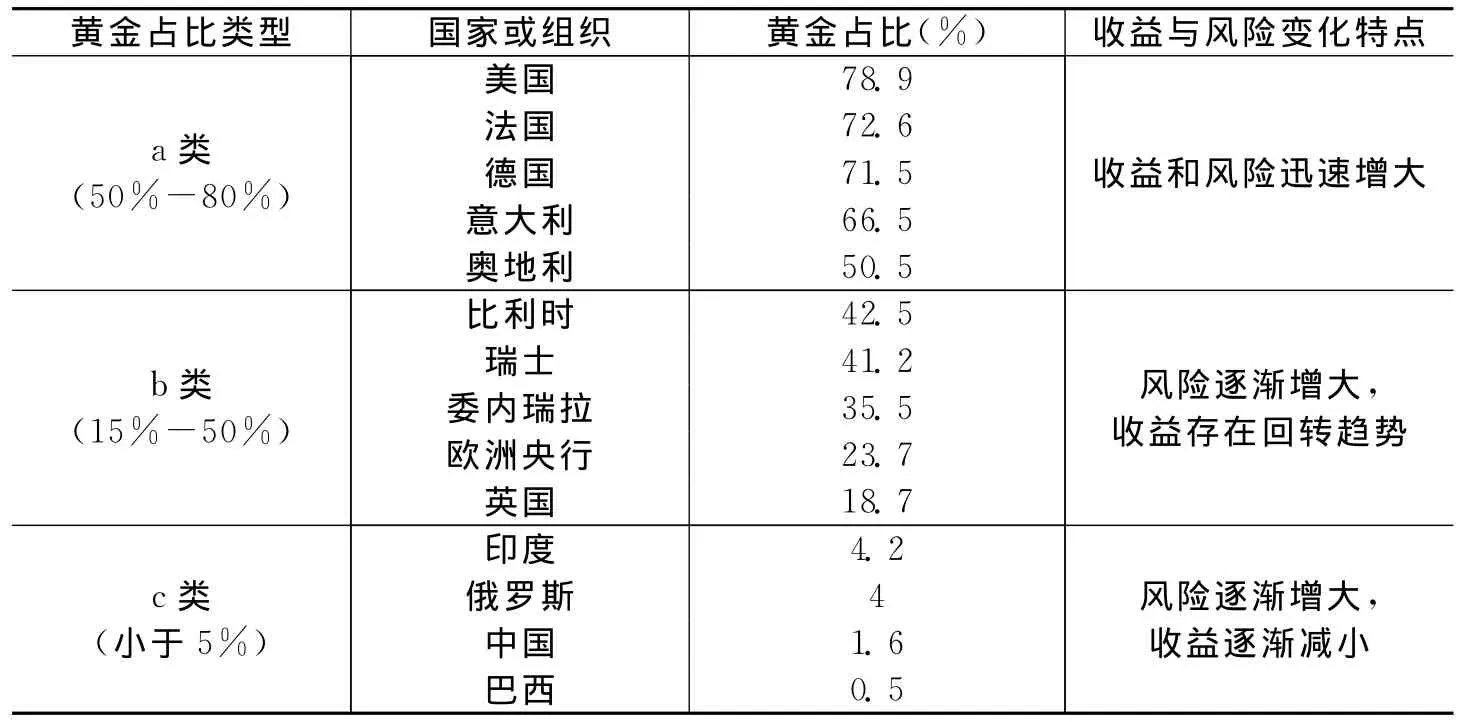
表5 黄金储备占比与各国收益和风险动态变化特点

通过上述分析可以看到，我国目前位于c类区间，持有的黄金储备在国际储备中占比过低，造成了较大的储备资产损失，并面临很大风险。以实际数据推算，2005年7月21日汇改时金价为422.15美元／盎司，美元／人民币汇率为8.27，而2011年5月30日，金价为1540.4美元／盎司，美元／人民币汇率为6.50。以本文研究结果的黄金占比23%和实际的1.6%进行对比，我国近期持有的价值总额为207 436.55亿元人民币的储备资产（依据2010年末我国黄金与外汇资产价值总额计算），经历汇改以来的美元贬值和金价上涨后，仅由黄金占比差异造成缩水92 425.66亿元人民币，人均7 109.66元人民币，差异非常显著。随着未来中国经济的发展，提升黄金储备至23%以上，相当于b类国家或地区的区间，从经济发展的状况看也具有一定的合理性，有利于减少我国经济对外汇储备的依赖，增强抵御货币金融冲击的能力。

五、结 语

在美元持续贬值和国际金价飙升的背景下，我国的国际储备中黄金占比仅为1.6%的结构亟待调整。本文研究为这种战略性转型提供了可供参考的理论与实证依据。本文构建组合资产的效用评估函数，使用T－Copula模型和Monte Carlo模拟来刻画黄金与美元资产的动态相依关系，计算组合资产的在险价值，通过极大化效用函数求解黄金在国际储备资产中的最优占比。在对外生参数和效用函数形式进行讨论后得出最优占比至少为23%。本文进一步对多个国家储备资产收益与风险变化进行动态和静态比较，发现不同类别的演化路径，而以金砖四国为代表的类别因黄金储备过低而正处于收益递减、风险增大的状态中。这说明我国亟须调整储备结构，加大黄金储备至优化区间。

注释：

①国际储备（International Reserve）指的是一国货币当局随时可利用并控制的外部资产（IMF，2009）。

②边缘推断法又称为两阶段极大似然法，可以较大程度地简化Copula的参数估计过程。

③考虑到一个国家的黄金储备最短调控周期至少为一周，并为了避免价格波动的“周末效应”，两列数据均取每周三的数值，共有539期。缺失值用相邻两期的平均值来补足。

④表中K－S统计值及其概率值是根据估计得到的条件边缘分布，对原序列残差做概率积分变换，再运用K－S检验方法，检验变换后的序列是否服从（0，1）均匀分布得到的。

［1］李述山.Copula－EGARCH模型及投资组合的时变风险价值估计［J］.山东科技大学学报（自然科学版），2010，（5）：97－101.

［2］黄恩喜，程希骏.基于pair copula－GARCH模型的多资产组合VaR分析［J］.中国科学院研究生院学报，2010，（4）：440－447.

［3］罗付岩，邓光明.基于时变Copula的 VaR估计［J］.系统工程，2007，（8）：28－33.

［4］王沁，王璐，何平.基于Spearmanρ的时变Copula模型的模拟及应用［J］.数理统计与管理，2011，（1）：76－84.

［5］韦艳华，张世英.Copula理论及其在金融分析上的应用［M］.北京：清华大学出版社，2008.

［6］张明恒.多金融资产风险价值的Copula计量方法研究［J］.数量经济技术经济研究，2004，（4）：67－70.

［7］Bartram S M，Taylor S J，Wang Y H.The Euro and European financial market dependence［J］.Journal of Banking and Finance，2007，31：1461－1481.

［8］Fantazzini D.Dynamic copula modelling for value at risk［J］.Frontiers in Finance and Economics，2008，5（2）：72－108.

［9］Capie F，Mills T，Wood G.Gold as a hedge against the US dollar［R］.Working Paper，World Gold Council，2004.

［10］Dempster N.Structural change in reserve asset management［R］.Working paper，World Gold Council，2009.

［11］Patton A J.Modelling asymmetric exchange rate dependence［J］.International Economic Review，2006，47：527－556.