基于区间直觉模糊集的研究型高校可持续发展能力评价

吴应宇 余德建

(东南大学经济管理学院，南京211189)

区间直觉模糊集是直觉模糊集的一种拓展形式，于1989年由 Atanassov和 Gargov［1］首次提出.由于区间直觉模糊集的隶属度、非隶属度和犹豫度用区间数表示，因此，与直觉模糊集相比，它能够更加细腻地描述和刻画客观世界的模糊性本质［2］.近年来，人们对区间直觉模糊集的研究取得了丰富的成果［3-5］.区间直觉模糊信息集成是区间直觉模糊集理论的重要组成部分.基于直觉模糊信息集成的思想［6-7］，区间直觉模糊信息集成研究也取得了一些成果.文献［8］提出了区间直觉模糊信息的加权算术(IIFWA)和加权几何集成算子(IIFWG)，并将其应用在多属性决策中.基于IIFWA算子，文献［9］研究了对方案有偏好的区间直觉模糊多属性决策方法.文献［10］提出了区间直觉模糊有序加权集成算子(IIFOWA)和混合集成算子(IIFHA).基于几何算子，文献［11］研究了区间直觉模糊有序加权几何算子(IIFOWG)和区间直觉模糊几何混合算子(IIFHG).在指标之间有关联的情况下，文献［12］把Choquet积分引入到区间直觉模糊信息集成中，提出了区间直觉模糊Choquet积分算子.文献［13］基于Sugeno积分，研究了区间直觉模糊信息的集成问题.

以上关于区间直觉模糊信息集成的研究基础是代数积与代数和，它们是一组T模和S模.然而任何T模与S模规则都可以运用到直觉模糊集的运算中［14］.文献［14-15］指出 Einstein 积与 Einstein 和也是一组T模和S模.本文受此启发，提出了新的区间直觉模糊信息集成算子，详细讨论其性质并与文献［8］中的区间直觉模糊信息集成算子做了对比分析.最后将提出的集成算子应用于决策领域，并提供一种基于区间直觉模糊信息的决策途径.

1 基于Einstein的区间直觉模糊运算法则

文献［1］在直觉模糊集的基础上首次提出区间直觉模糊集的概念.

定义1设X是给定的论域，则X上的区间直觉模糊集A定义为

式中，μA(x):→int(0，1)，vA(x):→int(0，1)分别为X中元素x属于A的隶属度和非隶属度，且满足

式中，int(0，1)为［0，1］区间所有闭子区间的集合.

文献［8］定义了区间直觉模糊数的概念，并且给出了区间直觉模糊数的一般表达形式(［a，b］，［c，d］)，满足［a，b］⊂［0，1］，［c，d］⊂［0，1］，b+d≤1.并且定义了为区间直觉模糊数的得分函数d)为区间直觉模糊数的精确度函数.进一步给出了2个区间直觉模糊数和的比较规则:

对于 2 个直觉模糊集 A=(μA，vA)和 B=(μB，vB).文献［14］定义了集合A和集合B的广义的交为 A∩B={x，T(μA，μB)，S(vA，vB)}，集合 A 和集合 B 广义的并为 A∪B={x，S(μA，μB)，T(vA，vB)}.其中 S(a，b)+T(1 － a，1 － b)≤1，∀(a，b)∈［0，1］，函数T为T模，函数S亦称为S模.因此任何T模与S模规则都可以运用到直觉模糊集的运算中.文献［14-15］指出Einstein积与Einstein和也是一组T模与S模，其中

Einstein积为

基于Einstein运算规则，本文定义新的区间直觉模糊数运算规则.

定义2设和为任意2 个区间直觉模糊数，则

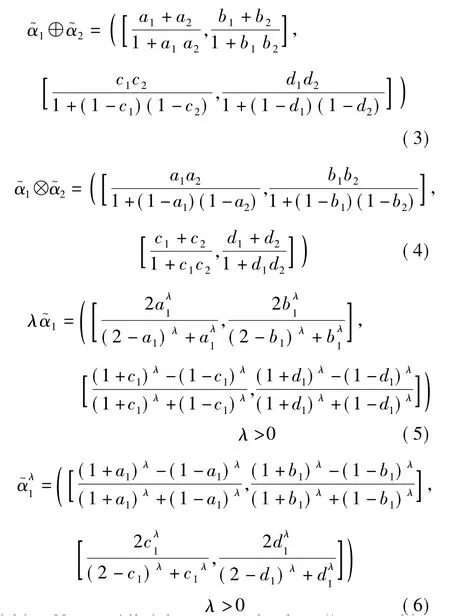
定理1设和(［a2，b2］，［c2，d2］)为任意 2 个区间直觉模糊数，λ＞0.则以下等式成立:

2 区间直觉模糊信息的集成算子

基于上述运算规则，给出区间直觉模糊数的Einstein加权几何算子.

定义3设为一组区间直觉模糊数，且设FIIFEWG:Ψn→Ψ，若

则称FIIFEWG为区间直觉模糊Einstein加权几何算子，其中 ω ={ω1，ω2，…，ωn}为的权重向量特别地，若则FIIFEWG算子退化为区间直觉模糊Einstein几何算子，即

定理2设为一组区间直觉模糊数，则由FIIFEWG算子得到的集成值仍为区间直觉模糊数，且

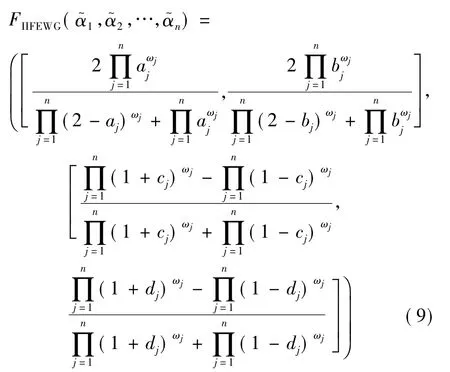
IIFEWG算子具有如下性质.

定理3设为一组区间直觉模糊数，且为的权重向量，则有

1)幂等性若即1，2，…，n，则

2)有界限 若

则

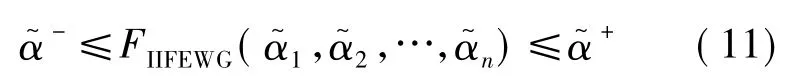
3)单调性设(j=1，2，…，n)为一组区间直觉模糊数，若对任意的 j，有，则

基于算术平均，下面给出区间直觉模糊数的Einstein加权算术平均算子的定义.

定义4设为一组区间直觉模糊数，且设FIIFEWA:Ψn→Ψ，若

则称FIIFEWA为区间直觉模糊Einstein加权算术算子，其中 ω ={ω1，ω2，…，ωn}为的权重向量

定理4设为一组区间直觉模糊数，则由IIFEWA算子得到的集成值仍为区间直觉模糊数，且

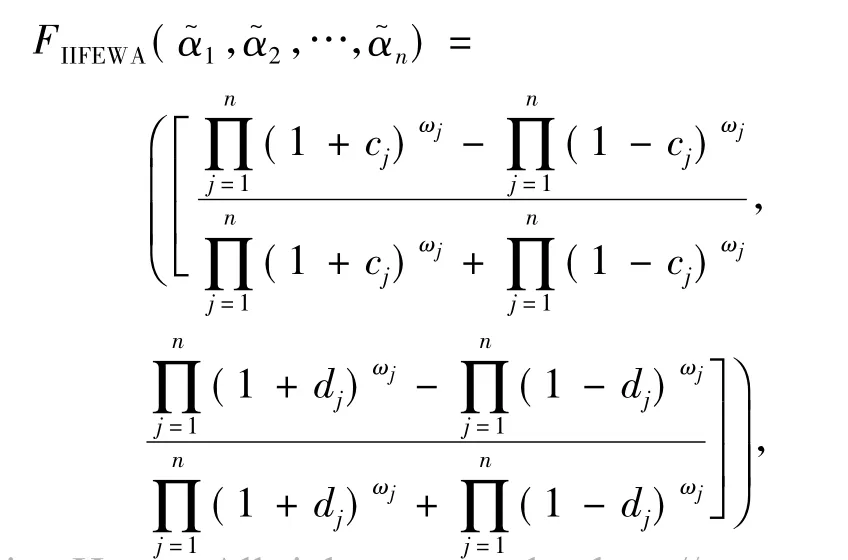
其中，ω ={ω1，ω2，…，ωn}为的权重向量

类似于 FIIFEWG算子，FIIFEWA算子也具有幂等性、单调性和有界性.

3 IIFEWG算子与IIFWG算子的比较

基于布尔代数运算规则，文献［8］提出了区间直觉模糊加权几何算子.一组区间直觉模糊数为的权重向量，ωj∈［0，1］(j=1，2，…，n)，，经IIFWG算子集成后为

定理5设为一组区间直觉模糊数，ω ={ω1，ω2，…，ωn}为的权重向量，则

成立［16］，则

同理可得

由于

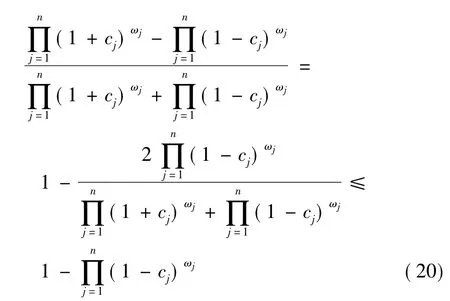
所以可得

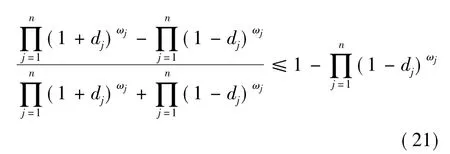
记

根据文献［12］中关于区间直觉模糊数大小的比较方法以及式(18)～(21)，可知 a≤e，b≤f，c≥g且d≥h.进而有

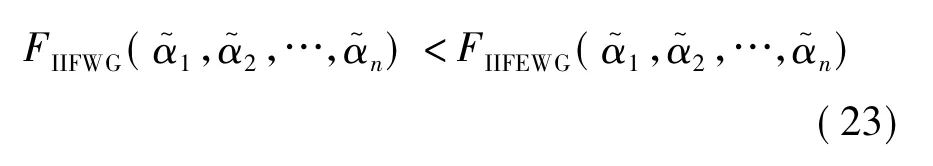
则有

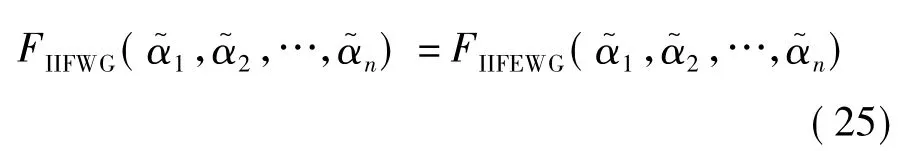
综合式(23)和(25)可以得到式(16)成立，即定理5成立.

4 基于IIFEWG算子的区间直觉模糊决策方法

设某一多属性决策问题，X={X1，X2，…，Xm}为候选方案集，C={C1，C2，…，Cn}为决策属性集.ω ={ω1，ω2，…，ωn}为属性权重向量，ωj∈［0，1］(j=.候选方案Xi在属性Cj下的特征信息用区间直觉模糊数α～ij=(［aij，bij］，［cij，dij］)表示，这样就可以得到决策矩阵A，如表1所示.

表1 区间直觉模糊决策矩阵A

基于IIFEWG算子，下面给出一种区间直觉模糊信息的决策方法，具体步骤如下:

①对区间直觉模糊决策矩阵进行标准化［17］.如果所有的属性都是效益型的，则不需要标准化;否则需要把决策矩阵标准化为 R=其中

②利用IIFEWG算子或者IIFEWA算子对决策矩阵R中的第i行的所有元素进行集结，得到候选方案Xi(i=1，2，…，m)的综合区间直觉模糊值

③根据区间直觉模糊数得分函数和精确度函数的定义计算直觉模糊值的得分函数和精确度函数

④根据区间直觉模糊数的比较规则对各方案进行排序，从而得到最佳方案.

5 研究型高校可持续发展能力评价

研究型高校作为高等教育事业的重要组成部分，在培养人才、促进经济发展等方面发挥着重要作用.经过多年的积累和发展，研究型高校虽然在规模、质量等方面取得了令人瞩目的成就，但就整体而言，仍处于缓慢发展的阶段，其国际竞争力更是让人担忧.因此，如何对研究型高校目前的可持续发展能力进行评价是一个亟待解决的现实问题.从高校的科研能力C1、人才培养 C2、财务发展潜力C3、财务当前水平 C4等4个属性来评价5所研究型高校Xi(i=1，2，…，5)的可持续发展能力.属性的权重向量为 ω ={0.1，0.2，0.4，0.3}.每所高校对属性的满足程度用区间直觉模糊数表示，所得的区间直觉模糊数决策矩阵为R，如表2所示.IIFEWG算子对5所高校的可持续发展能力进行评价的具体步骤如下:

表2 区间直觉模糊决策矩阵R

1)由于科研能力C1、人才培养 C2、财务发展潜力C3、财务当前水平 C4均为效益型指标，因此不需要标注化.

2)这里利用IIFEWG算子对决策矩阵R中的第i行的所有元素进行集结，得到候选方案Xi(i=1，2，…，5)的综合区间直觉模糊值分别为

如果利用文献［8］中的IIFWG算子对5所高校的可持续发展能力进行评价，具体步骤如下:

①与步骤1)相同.

6 结语

区间直觉模糊集利用区间数来表示直觉模糊集中的隶属度、非隶属度和犹豫度，从而能更加灵活地表达不确定信息.本文基于Einstein运算规则，研究了区间直觉模糊信息的集成问题，提出了区间直觉模糊Einstein加权几何算子.研究了其性质并和已有的集成算子进行比较研究，指出了IIFEWG算子与已有集成算子之间的关系，并将其应用多属性决策中，从而丰富和发展了区间直觉模糊集理论.

References)

［1］Atanassov K T，Gargov G.Interval-valued intuitionistic fuzzy sets［J］.Fuzzy Sets and Systems，1989，31(1):343-349.

［2］Xu Z S.On similarity measures of interval-valued intuitionistic fuzzy sets and their application to pattern recognitions［J］.Journal of Southeast University:Natural Science Edition，2007，23(1):139-143.

［3］徐泽水.直觉模糊集成理论及应用［M］.北京:科学出版社，2008.

［4］Xu Z S，Cai X Q.Incomplete interval-valued intuitionistic fuzzy preference relations［J］.International Journal of General Systems，2009，38(8):871-886.

［5］Xu Z S.Approaches to multiple attribute group decision making based on intuitionistic fuzzy power aggregation operators［J］.Knowledge-Based Systems，2011，24(6):749-760.

［6］Xu Z S.Intuitionistic fuzzy aggregation operators［J］.IEEE Transactions on Fuzzy Systems，2007，15(6):1179-1187.

［7］Xu Z S，Yager R R.Some geometric aggregation operators based on intuitionistic fuzzy sets［J］.International Journal of General Systems，2006，35(4):417-433.

［8］徐泽水.区间直觉模糊信息的集成方法及其在决策中的应用［J］.控制与决策，2007，22(2):215-219.Xu Zeshui.Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making ［J］.Control and Decision，2007，22(2):215-219.(in Chinese)

［9］卫贵武.对方案有偏好的区间直觉模糊多属性决策方法［J］.系统工程与电子技术，2009，31(3):116-120.Wei Guiwu.Method for interval-valued intuitionistic fuzzy multiple attribute decision making with preference information on alternatives［J］.Systems Engineering and Electronics，2009，31(3):116-120.(in Chinese)

［10］徐泽水，陈剑.一种基于区间直觉判断矩阵的群决策方法［J］.系统工程理论与实践，2007，27(4):126-133.Xu Zeshui，Chen Jian.Approach to group decision making based on interval-valued intuitionistic judgment matrices［J］.Systems Engineering-Theory and Practice，2007，27(4):126-133.(in Chinese)

［11］Xu Z S.A survey of preference relations［J］.International Journal of General Systems，2007，36(2):179-203.

［12］Xu Z S.Choquet integrals of weighted intuitionistic fuzzy information［J］.Information Sciences，2010，180(5):726-736.

［13］武建章，张强，桑圣举.基于Sugeno积分的区间直觉模糊多属性决策［J］.北京理工大学学报，2010，30(5):608-612，621.Wu Jianzhang，Zhang Qiang，Sang Sengju.Sugeno integrals for multi-criteria decision making with interval intuitionistic fuzzy information［J］.Transactions of Beijing Institute of Technology，2010，30(5):608-612，621.(in Chinese)

［14］Deschrijver G，Cornelis，Kerre E E.On the representation of intuitionistic fuzzy t-norms and t-conorms［J］.IEEE Transactions on Fuzzy Systems，2004，12(1):45-61.

［15］Wang W Z，Liu X W.Intuitionistic fuzzy geometric aggregation operators based on einstein operations［J］.International Journal of Intelligent Systems，2011，26(11):1049-1075.

［16］Xu Z S.On consistency of the weighted geometric mean complex judgment matrix in AHP［J］.European Journal of Operational Research，2000，126(3):683-687.

［17］Xu Z S，Hu H.Projection models for intuitionistic fuzzy multiple attribute decision making［J］.International Journal of Information Technology and Decision Making，2010，9(2):267-280.