基于面部曲线特征融合的三维人脸识别

邹红艳 达飞鹏 李晓莉

(1东南大学自动化学院，南京210096)

(2南京林业大学机械电子工程学院，南京210037)

人脸识别作为一种重要生物特征识别方法，具有对用户干扰少、易被接受等特点，在生物认证中具有广阔的应用前景.三维人脸识别主要根据人脸的三维几何形状信息进行识别，且不会受姿势和光照的影响.随着三维扫描技术快速发展，三维人脸识别得到了越来越多的关注［1-2］.

目前有关三维人脸识别方法的研究有很多，可以分为基于整体特征、基于局部特征和基于整体特征局部特征相融合的方法.基于整体特征的人脸识别方法将整张人脸区域作为一个整体进行变换或提取特征，然后进行匹配识别.Srivastava等［3］首先将网格人脸映射为深度图像，采用随机梯度算法训练最大化类间距离的正交基底，然后将高维人脸映射到该低维空间中，再用最近邻法对人脸进行识别.Llonch等［4］将三维人脸点云映射到一个二维球面中，然后采用LDA对二维球面人脸图像进行分析.然而整体特征提取时易受姿势变化的影响，同时基于整体特征的方法无法很好处理头发、胡子等遮挡的影响.基于局部特征的方法利用人脸部分区域的特征进行识别，该方法可以对人脸的不同区域根据其特性进行不同对待，因此在处理表情和遮挡等问题时，与基于整体的方法相比具有一定的优势.ter Haar等［5］分别以鼻尖点为中心，提取人脸等测地距离轮廓线、等欧氏距离轮廓线、平面内等欧氏距离轮廓线和等深度轮廓线，分析不同轮廓线对人脸的不同表征性.Berretti等［6］提取到鼻尖点等距离的点组成等测地轮廓带，计算等测地轮廓带之间的3D Weighted Walkthroughs(3DWWs)特征进行识别.然而基于局部特征的方法一般易受噪声点的影响.

单纯基于整体特征或局部特征的人脸识别方法都存在一定的局限性.因此本文从这个角度出发，首先在姿势校正后的人脸上提取到鼻尖点测地距离相等的等测地轮廓线，然后分别从轮廓线上点的局部邻域信息和轮廓线整体形状信息角度提取人脸局部和整体特征进行识别，最后对比较结果采用加权求和规则进行融合，利用最近邻分类器获得最终识别结果.实验证明，本文算法在表情鲁棒性和识别率上都体现了比较好的性能.

1 预处理与轮廓线提取

1.1 人脸数据预处理

为了准确提取特征，需对人脸进行切割和姿势矫正以得到严格的人脸区域.本文参照文献［1］的方法，首先根据人脸形状指数［7］特征和几何约束条件确定鼻尖点p位置，然后以鼻尖点为中心，以半径r=90 mm做球体，球体内包含的人脸区域即为切割的人脸区域.原始人脸和切割后的人脸如图1(a)和(b)所示.

图1 人脸切割和姿势矫正

对切割后的人脸点云进行主成分分析(PCA)，可得到3个互相垂直的主方向，将最大特征值对应的特征向量作为新坐标系的y轴，最小特征值对应的特征向量作为z轴，建立右手坐标系，在该坐标系下人脸应具有相同的正面姿态.该坐标系也被称为姿势坐标系(pose coordinate system，PCS)［8］.以鼻尖点 p作为 PCS的原点，将切割后的人脸点云数据都转换到PCS中，即完成人脸姿态校正，如图1(c)所示.

1.2 等测地轮廓线提取

曲面上2点之间的最短距离即为测地距离，它被认为是不随着人脸表情的变化而改变的［9］.本文采用由Dijkstra［10］提出的方法计算人脸点云上任意2点的测地距离.

计算人脸所有点到鼻尖点的测地距离之后，选择到鼻尖点测地距离在［γ－δ，γ+δ］范围内的点组成等测地轮廓线.在本文中取δ=1.4 mm，且根据不同参数γ值在人脸区域等间隔提取17条等测地轮廓线 c'γ(i)(i=1，2，…，17)，如图 2(a)所示.

图2 等测地轮廓线提取及采样

1.3 等测地轮廓线采样

在特征匹配前需要对等测地轮廓线c'γ(i)进行重新采样.以鼻尖点为中心构造一个椭圆，方程如下:

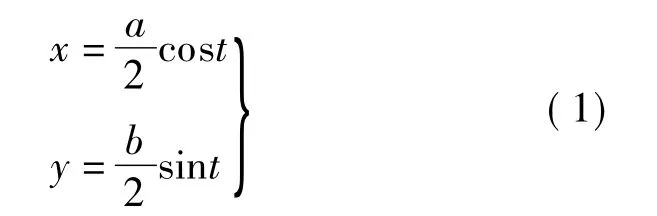
式中，t=［0，2π］;a 为 c'γ(i)在 x 轴方向的投影差值;b为c'γ(i)在y方向的投影差值.通过离散采样t，可以在椭圆上采样不同数目的点.

对于椭圆上每一个采样点，在等测地轮廓线上选取距离最近的点作为测地轮廓线采样点.图2(b)和(c)分别显示了采样前、后的等测地轮廓线.

2 局部特征匹配

2.1 局部特征提取

取重采样后的等测地轮廓线cγ(i)上任一点p，以p为中心，r=10 mm为半径做球体，球体内包含的人脸区域即为点p的邻域L.利用PCA计算邻域点云L的主轴，将与最大特征值对应的特征向量作为y轴，与最小特征值对应的特征向量作为z轴，建立一个右手坐标系，并将坐标系的原点设在点云质心o.

点集L中的每个点li在新坐标系下的投影坐标为［x'i，y'i，z'i］T.邻域 L 中的点在 3 个轴上的投影值可分别组成一个列向量 Lx=［x'1，x'2，…，x'na］T，Ly=［y'1，y'2，…，y'na］T和 Lz=［z'1，z'2，…，z'na］T.

分别提取点云在3个主轴方向的最大投影和最小投影值之间的差值fx，fy和fz.其中fz反映了点集曲面的弯曲度，但无法通过fz确定曲面L是凹的还是凸的.通过点p的z坐标对fz进行了修正.设点p 在新局部坐标系中的坐标为［p'x，p'y，p'z］T，则修正后的fz为

图3即为提取的特征fx，fy和f'z.除此之外，还提取了邻域L的面积s作为本文所用局部特征.［fx，fy，f'z，s］T即为在点 p 提取的局部特征.

图3 局部特征fx，fy和f'z

2.2 局部特征匹配

对等测地轮廓线cγ(i)上每一点进行局部特征提取，得到轮廓线 cγ(i)的局部特征 Lcγ(i)=［l1，l2，…，lncγ(i)］，其中 ncγ(i)为采样后的轮廓线 cγ(i)中点的个数

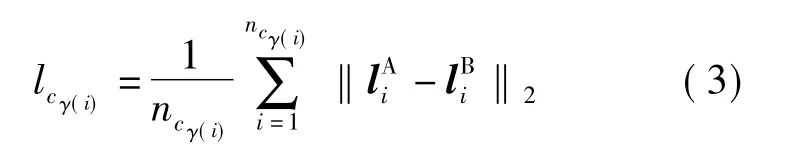
式中，ncγ(i)为轮廓线中的点数;为人脸A在第i点的局部特征;为人脸B在轮廓线中与人脸A在轮廓线中第i点的对应点的局部特征.

1)建立点对应的关系

根据式(3)计算轮廓线相似性，首先需要确定不同人脸的对应轮廓线和的对应点对.假设的第1个点与轮廓线的第 j个点对应(2≤j≤ncγ(i))，则中的第i个点在中的对应点为第k个，其中k可通过下式获取:

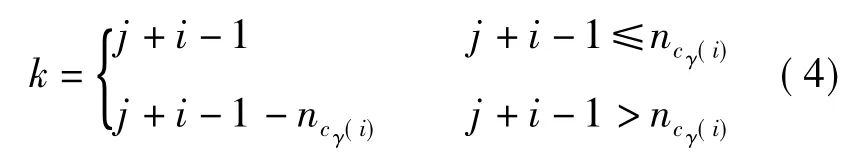
采用上述方法共建立了ncγ(i)种点对应关系.对于每一种点对应关系，根据式(3)可以获取一个相似性度量.考虑人脸的形状信息，取具有最小特征距离时的对应点为合理的点对应关系，且此时的最小特征距离scγ(i)即为人脸A和B对应轮廓线和的相似性度量.

2)局部特征比较

对不同的轮廓线根据其到鼻尖点的距离设定一个权值ωcγ(i)，越靠近鼻尖点的轮廓线，具有越大的权值.ωcγ(i)的计算式为

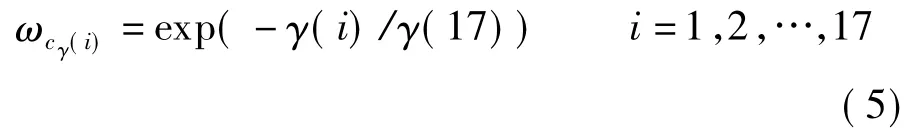
式中，γ(i)为第i个参数的γ值.

最后将17条等测地轮廓线匹配结果融合，则得到由局部特征得出的人脸相似度为

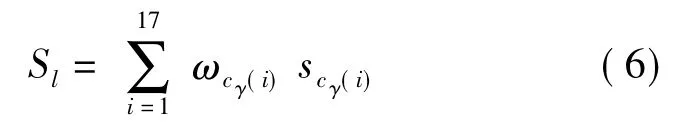
3 全局特征匹配

3.1 整体特征提取

将轮廓线cγ(i)分别向姿势坐标系PCS的x，y轴方向投影，投影值组成2个向量xproj和yproj.分别将这2个向量最大值与最小值的差值作为轮廓线在x，y轴方向的整体特征(见图4)，即

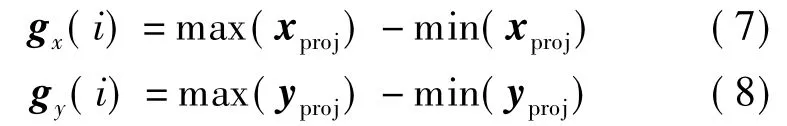
选取轮廓线 cγ(i)的整体特征为 gi=［gx(i)，gy(i)］.

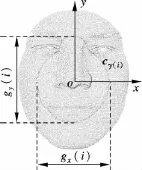
图4 等测地轮廓线整体特征

3.2 整体特征匹配

采用上述方法分别对人脸的17条等测地轮廓线进行比较，可以得到17个表示相似性的度量gcγ(i)(1≤i≤17).利用式(5)计算权值 ωcγ(i)，对各轮廓线结果加权求和，得出整体特征相似度为

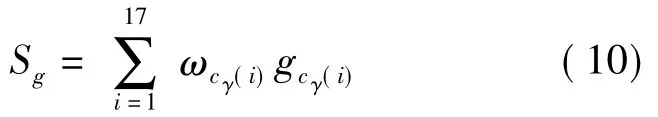
3.3 局部和整体特征融合

对于具有N个模型的库集，将分别得到N维表示局部特征和整体特征相似度的向量SL和SG，SL=［Sl1，Sl2，…，SlN］，SG=［Sg1，Sg2，…，SgN］.分别对向量SL和SG按照最大-最小原则归一化，即

然后对归一化后的局部和整体相似度向量采用加权求和规则融合，即

式中，ωl=ωg=0.5.最后选取S中最小元素对应的库集人脸作为识别对象.

4 实验结果与分析

FRGC v2.0是一个大型的公共人脸数据库［11］，其中的三维人脸数据集是目前世界上最大的三维人脸数据库，人脸数据为三维点云.在FRGC v2.0数据库中选取41人的人脸数据，共241张来进行试验.将每个人的一幅中性表情人脸(共41张)组成库集;剩余200张人脸组成测试集，包含无表情人脸112张和有表情人脸88张.

4.1 基于特征融合的识别结果

按照本文介绍的方法，分别提取库集和测试集人脸的局部及整体特征并进行融合，进行识别试验，得到的 CMC(cumulative match characteristic)曲线如图5所示.由图可知，使用整体特征和局部特征进行识别，在级数为1时的识别率分别为80.1%和92.3%，而融合了局部特征和整体特征后的识别率达到96.2%，说明这种特征融合方法可取得较好的识别效果.

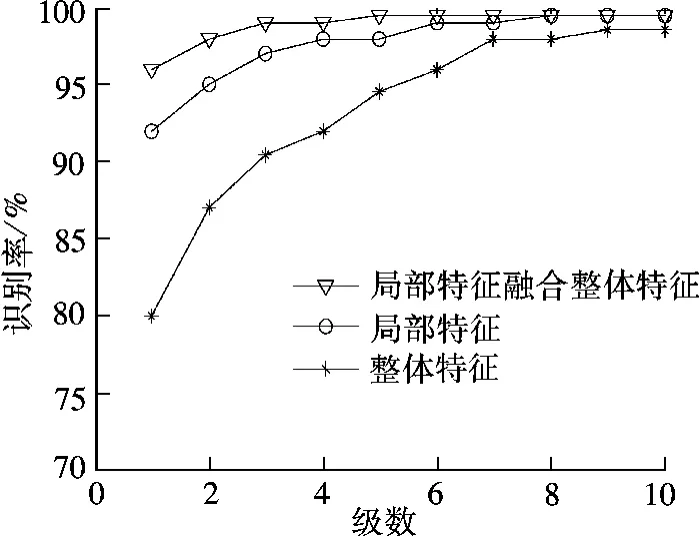
图5 CMC曲线

4.2 表情鲁棒性实验

将测试集人脸中的112张无表情人脸和88张有表情人脸分别和库集人脸进行识别实验，实验结果见图6.

图6 不同特征的表情鲁棒性

由图6可知，中性表情人脸在采用局部特征、整体特征和本文方法融合后特征的识别率分别为97.3%，91.1%和99.1%.与中性表情人脸相比，有表情人脸在这3种特征下的识别率普遍较低，分别为87.5%，63.6%和93.2%.但采用本文方法时识别率仅降低了5.9%，远小于另外2种方法，说明本文采用的特征融合后的方法对于表情变化具有较好的鲁棒性.

5 结语

本文提出了一种结合局部特征和整体特征的三维人脸识别方法.该方法首先提取人脸等测地轮廓线，通过分析轮廓线上点的局部点云分布信息和面积特征，提取不依赖于坐标信息的局部特征，并依据轮廓线形状信息提取人脸整体特征，分别比较局部特征和整体特征，最后对结果进行融合.在FRGC v2.0数据库中验证本文算法的性能，实验结果证明了该方法的有效性，且对表情变化有一定鲁棒性.

References)

［1］李晓莉，达飞鹏.基于排除算法的快速三维人脸识别方法［J］.自动化学报，2010，36(1):153-158.Li Xiaoli，Da Feipeng.A rapid method for 3D face recognition based on rejection algorithm［J］.Acta Automatica Sinica，2010，36(1):153-158.(in Chinese)

［2］Bowyer K W，Chang K，Flynn P J.A survey of approaches and challenges in 3D and multi-modal 3D+2D face recognition［J］.Computer Vision and Image Understanding，2006，101(1):1-15.

［3］Srivastava A，Liu Xiuwen，Hesher C.Face recognition using optimal linear components of range images［J］.Image and Vision Computing，2006，24(3):291-299.

［4］Llonch R S，Kokiopoulou E，Tosic I，et al.3D face recognition with sparse spherical representations［J］.Pattern Recognition，2010，43(3):824-834.

［5］ter Haar F B，Veltkamp R C.A 3D face matching framework for facial curves［J］.Graphical Models，2009，71(2):77-91.

［6］Berretti S，del Bimbo A，Pala P.3D face recognition using isogeodesic stripes［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32(12):2162-2177.

［7］Dorai C，Jain A K.COSMOS-A representation scheme for 3D free-form objects［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19(10):1115-1130.

［8］Zhang L Y，Razdan A，Farin G，et al.3D face authentication and recognition based on bilateral symmetry analysis［J］.Visual Computer，2006，22(1):43-55.

［9］Bronstein A M，Bronstein M M，Kimmel R.Three-dimensional face recognition［J］.International Journal of Computer Vision，2005，64(1):5-30.

［10］Dijkstra E W.A note on two problems in connection with graphs［J］.Numerische Mathematic，1959，1(3):269-271.

［11］Phillips P J，Flynn P J，Scruggs T，et al.Overview of the face recognition grand challenge［C］//Proceedings of 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.San Diego，USA，2005:947-954.