大尺度钢筋混凝土双向板的受拉薄膜效应分析

张大山 董毓利 朱崇绩

(1哈尔滨工业大学土木工程学院，哈尔滨150090)

(2华侨大学土木工程学院，泉州362021)

(3济南大学土木建筑学院，济南250022)

大量研究表明，薄膜效应的存在使钢筋混凝土板在大变形下的实际承载力比经典塑性铰线理论(又称屈服线理论)的计算结果大得多.混凝土板在正常使用情况下，一般处于弹性小变形状态，此时产生的受压薄膜效应可以在一定程度上提高板的承载力，在进行板的设计时若加以考虑可节省钢筋和混凝土用量.相比之下，在大变形情况下才产生的受拉薄膜效应的优势并不明显.然而，随着建筑结构抗火研究的深入，人们意识到建筑结构遭遇火灾、爆炸等偶然作用时，只要不发生坍塌或者丧失整体性，板发生较大的挠度是可以接受的.近年来，国内外学者针对双向板的薄膜效应及其在抗火设计中的应用进行了大量研究［1-5］.对比国内外文献发现，以往的混凝土板力学性能试验研究主要针对板的正常使用极限状态和承载力极限状态，一般当形成塑性铰线模式时即停止试验，并且进行的多为模型试验［6-7］.

Dong等［8］基于经典塑性铰线理论提出了计算钢筋混凝土板大变形时极限承载力的板块平衡法，并利用文献［6］中的缩尺试验进行了验证.挠度变形是板力学性能的重要参数，也是板能产生受拉薄膜效应的关键因素.板的尺寸、钢筋和混凝土的材性以及彼此间的黏结滑移特性等都对变形的发展有显著影响，因此利用缩尺试验研究板的受拉薄膜效应具有一定的局限性.

本文首先分析了板块平衡法中假设条件的局限性;然后，选取2块大尺度钢筋混凝土矩形板和2块大尺度钢筋混凝土方形板，在大挠度加载下进行力学性能试验，得到了双向板的荷载-挠度曲线，并对塑性铰线模式进行了分析;最后，根据大尺度试验数据，修正了混凝土板挠度特征值的计算公式，并将修正的板块平衡法的计算结果与已有的试验数据进行了对比.

1 板块平衡法

文献［8］认为，在大挠度下板的受拉薄膜效应由各个塑性铰线截面处钢筋合力的竖向分量引起，并给出了矩形板和方板的承载力计算公式.

板块平衡法只考虑了塑性铰线模式与支座之间板块的平衡.在建立平衡方程时，考虑塑性铰线截面处钢筋合力的竖向分量，可得到矩形板承载力的计算公式为

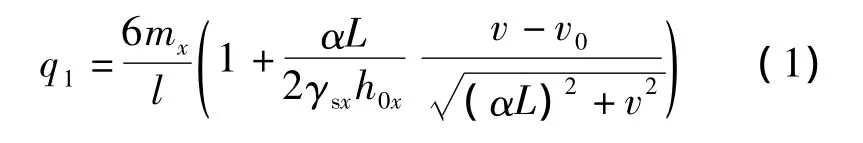
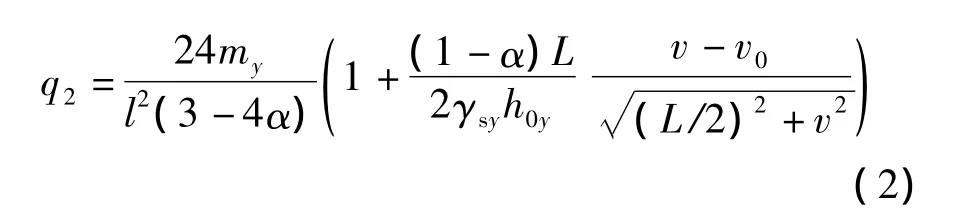
式中，q1，q2分别为矩形板被塑性铰线分成的梯形板块和三角形板块上的极限承载力;mx，my分别为x，y方向上每单位长度塑性铰线上的抵抗矩;L，l分别为板的长、短向跨度;α为塑性铰线的位置参数;λ为特征比，且λ=L/l;h0为钢筋的有效高度;v为板的挠度;v0为形成塑性铰线时的挠度;γsx，γsy分别为x，y方向上钢筋合力点到混凝土合力点之间的距离系数，一般取值为 0.85 ～0.90［9］.

一般地，q1≠q2，则矩形板的极限承载力qr为

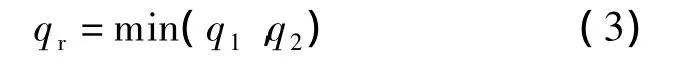
同理，方形板的极限承载力qs为

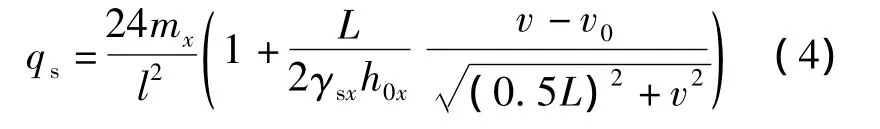
文献［1］假设在钢筋平均应力达到0.5fy时，混凝土板达到最大挠度vmax，即

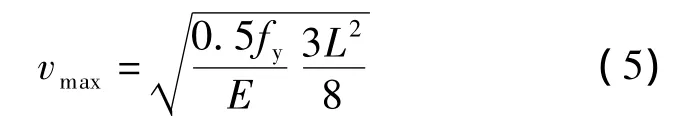
式中，fy为钢筋屈服强度;E为钢筋的弹性模量.

文献［8］中，假定钢筋平均应力为0.1fy时板形成塑性铰线模式，此时挠度v0为

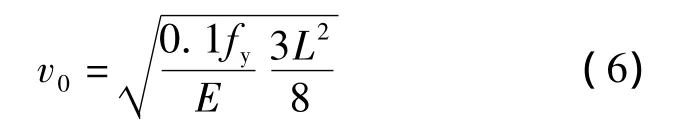
v0和vmax统称为板块平衡法的挠度特征值，是计算混凝土板受拉薄膜效应的关键参数.

假定矩形板和方形板的受拉薄膜效应是在塑性铰线形成后才开始变得显著的.当挠度v＜v0时，式(1)、(2)和(4)变为经典屈服线理论的计算公式，即计算时可代入v=v0;当挠度v≥v0时，钢筋合力的竖向分量随着挠度的增大而逐渐增大，当v=vmax时，即可求得板的极限承载力qmax.

基于 Bailey等［6］的双向板数据，文献［8］对板块平衡法的有效性进行了验证，但验证结果中存在部分试验数据与分析结果误差较大的情况.其原因在于:① 采用的数据来源于缩尺试验结果;② 形成塑性铰线模式的挠度v0是基于经验假设而定的，未经试验验证.本文选取了4块大尺度混凝土双向板(包括2块矩形板和2块方形板)进行大挠度下的静力加载试验，对上述问题进行验证.

2 试验概况

试验中2块矩形板的编号分别为JXB-1和JXB-2，2块方形板的编号分别为FXB-1和FXB-2，其主要参数见表1.各试件均为简支边界条件，部件组成及安装如图1所示.混凝土保护层厚度为15 mm，加载系统的自重为9.0 kN.为测试底部受力钢筋的受力特性，在制作试件时，预先将应变片粘贴在板底2个方向上受力钢筋的跨中部位.

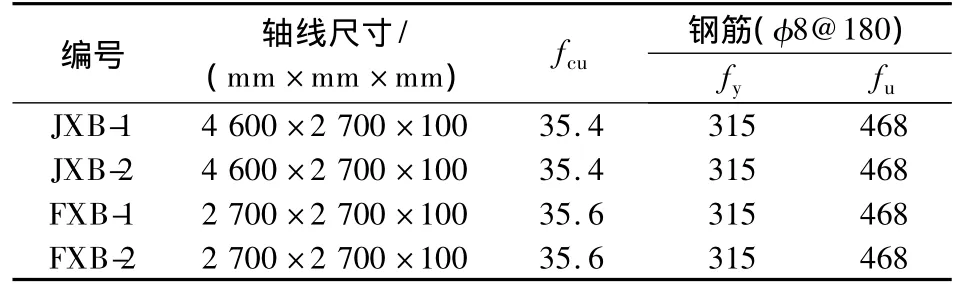
表1 试件的主要参数

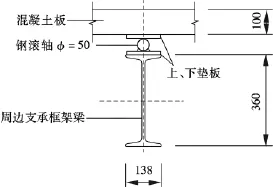
图1 简支边界的安装示意图(单位:mm)

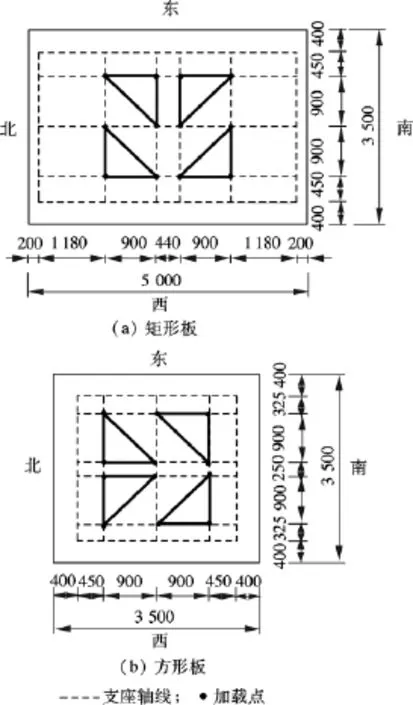
图2 加载点布置(单位:mm)

试验中采用12个加载点近似模拟均布荷载.矩形板和方形板的加载点布置有所不同(见图2).为防止应力集中导致混凝土局部压坏，在加载点处设置厚度为10 mm的钢垫板.《混凝土结构试验方法标准》［10］中判断受弯试件达到承载力极限状态的标准包括:①有明显屈服平台的热轧钢筋，并且受拉主钢筋应力达到屈服强度，受拉应变达到0.01;②受拉主钢筋拉断;③ 受拉主钢筋处最大垂直裂缝宽度达到1.5 mm;④ 挠度达到跨度的1/50;⑤受压区混凝土压碎.为确保试验板进行大挠度加载，本试验不以上述现象作为加载终止标志，而以混凝土板的挠度达到长向跨度的1/20或者出现不适于加载的危险状况作为试验终点.该处的变形控制值选取为长向跨度的1/20，这是基于混凝土板火灾试验的破坏准则确定的［11］.

试验采用液压千斤顶加载，连续慢速加载直至试件破坏.试验板的全景见图3.

图3 试验全景

3 试验结果与分析

3.1 试验现象

矩形板和方形板各自的2个试件在外荷载作用下表现的力学性能相似，故本文以每组试件的第2块板为例，描述试验现象.文中的荷载大小为板面上各集中力的总和，可以根据跨中弯矩相等的原则，将其与均布荷载进行转换.加载过程中，各试件受压区混凝土未压碎，钢筋也未出现拉断现象.

对于矩形板而言，当荷载加至27 kN时，板底跨中沿着长跨方向开始出现裂缝.当荷载加至105 kN时，图4(a)中裂缝a的宽度达到1.5 mm.当荷载加至300 kN时，虽然板底混凝土已经脱落许多，钢筋开始裸露，但混凝土板仍能稳定地承担荷载，甚至在挠度超过长跨跨度的1/20时仍未出现承载力下降的迹象.

对于方形板而言，当荷载加至29 kN时，板底开始出现裂缝;当荷载加至180 kN时，板底裂缝宽度达到1.5 mm;当荷载加载至250 kN时，底部混凝土开始脱落，受力钢筋开始裸露.

由此可见，矩形板和方形板板底的裂缝簇模式与经典的屈服线理论假设的塑性铰线模式一致.

图4 板底裂缝

3.2 钢筋应变

混凝土板底配有单层钢筋网.定义底层的钢筋方向为x方向，上层的钢筋方向为y方向.图5为钢筋的跨中应变与荷载的关系曲线.由图可知，当矩形板和方形板的荷载分别达到119和184 kN时，其各自板底x方向的钢筋屈服.根据式(1)，(2)和(4)可计算得到矩形板和方形板的屈服线理论强度分别为118和201 kN.当荷载达到经典屈服线理论计算的极限强度值时，板底钢筋正好屈服或者刚屈服.虽然此时观测的裂缝形态与经典屈服线理论假定的模式一致，但各个塑性铰线截面处的板底钢筋并未全部屈服，尚具有较高的承载力提高空间.

图5 荷载-跨中钢筋应变曲线

文献［8］认为，挠度超过式(6)计算的v0时，受拉薄膜效应开始变得显著，且已形成塑性铰线.结合观测的试验宏观现象可知，当荷载超过经典屈服线理论值后，挠度增长速度加快，塑性铰线处钢筋合力的竖向分量变得越来越显著.因此，假定当荷载达到经典屈服线理论值时，对应的挠度取为v0是可行的.但此时塑性铰线并未正式形成，建议将v0称为受拉薄膜效应开始显著时的挠度较为妥帖.

3.3 荷载-挠度曲线

图6为各试件的荷载-挠度曲线以及板块平衡法计算的理论曲线.

图6 荷载-挠度曲线

由各板的荷载-挠度曲线及观测的试验现象可得各种荷载特征值(见表2).表中，Fsy为板底跨中钢筋刚屈服时的荷载值;Fc为裂缝宽度达到1.5 mm时的荷载值;FL/50为挠度达到L/50时的荷载值;Fmax为实测的极限强度值;Fu为由一般承载力极限状态破坏标准所得的极限荷载值，是Fsy，Fc，FL/50中的最小值.在试验进行中，各板均未出现混凝土被压碎和底部受拉钢筋拉断的现象.

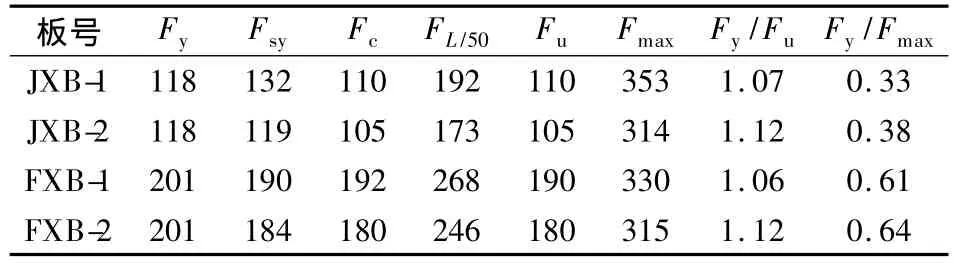
表2 各特征点的荷载值 kN

由表2可知，各个试件的极限承载力Fu与经典塑性铰线理论值Fy吻合较好.然而，当荷载达到Fy时，各板的承载力仍有较大的提高空间.经典屈服线理论虽然是一种上限解，但不能解释混凝土板极限承载力提高的原因.对于矩形板而言，当外荷载达到228 kN时，挠度为143 mm(约L/32)，板底混凝土脱落较为严重，呈现破坏状态，但板仍能继续稳定地承担更大的荷载，直至挠度超过L/20.对于方形板而言，当荷载加至304 kN时，挠度为103 mm(约L/26)，板底混凝土脱落也较为严重，且荷载-挠度曲线呈现一小段平滑段，挠度增加较快，随之达到承载力的最大值.然而，方形板的挠度未达到L/20时，承载力已开始逐渐下降.

4 计算方法验证

文献［8］提出了考虑受拉薄膜效应的计算混凝土板极限承载力的板块平衡法，并利用文献［6］中的缩尺试验数据对该方法的有效性进行了验证.该方法中v0和vmax的计算公式均是基于经验假设提出的.在文献［6］中，根据试验结果已指出式(5)计算的vmax值较为保守.该值与本文数据也不吻合，理论值仅为实测值的1/3(见表3).基于此，在计算承载力时采用实测挠度值，将荷载达到经典屈服线理论值时所对应的挠度作为v0的实测值，建立荷载-挠度的相关曲线，计算结果见图6.由图可知，矩形板的理论值计算结果精度优于方形板，方形板的理论值略显保守.为便于工程设计使用，需进一步确定v0和vmax的准确计算公式.

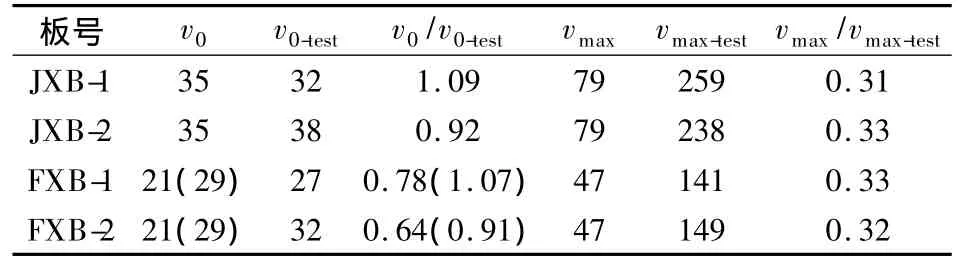
表3 各特征点的挠度值 mm

4.1 v0的确定

v0的计算公式是文献［8］基于式(5)的形式提出的，未经试验验证.各试件在达到经典屈服线理论值时的挠度值v0-test较小，远小于板的最大挠度值.试件的安装及加载等工序对v0-test的数据采集具有较为显著的影响.因此，矩形板的v0与v0-test偏差10%是可以接受的.但方形板的v0/v0-test都偏小，显得较为保守.若将式(6)中的0.1修正为0.2，结果见表3中的括号内数值.修正后的公式为

可见，利用式(7)计算方形板受拉薄膜效应开始显著的挠度是可行的.但对于矩形板而言，仍然采用式(6).

4.2 vmax的确定

采用式(5)计算混凝土板所能达到的最大挠度vmax是保守的.实际上，板所能达到的最大挠度值与诸多因素有关，如钢筋和混凝土的材性及其相互之间的黏结滑移特性等.加载至试验后期，板底混凝土脱落较为严重，此时板已不再适于加载，若认为此时板已达到最大承载力，则矩形板和方形板的挠度分别约为L/32和L/26.当混凝土板接近最大挠度时，板内钢筋的工作状态与挠度达到v0时不同，这是因为此时板内跨中已有较多钢筋在中部较大范围内屈服，并且钢筋与混凝土间的黏结力也较弱.因此，确定vmax的计算公式可不考虑钢筋的力学性能影响.根据已有试验结果，为便于工程设计和偏于安全的考虑，假定板所能达到的最大挠度可简单地统一取为L/40，即

4.3 理论验证

基于文献［6-7］的结果以及本文的试验数据，将式(7)和(8)分别代入式(3)和(4)，计算双向板的极限承载力，结果见表4.表中，Pcal和Ptest分别为板块平衡法的理论值和试验值.由表可知，修正的板块平衡法能较好地计算大挠度下混凝土板的极限承载力.由于缩尺试验和大尺度试验的尺寸效应，利用该方法计算文献［6］中个别数据时误差相对较大，而计算文献［7］及本文数据时误差相对较小.在表4中，Pcal/Ptest的均值和变异系数分别为1.02和0.097，由此可知，修正后板块平衡法的计算精度较好.在板块平衡法中采用修正的挠度特征值计算公式，可计算得到双向板的荷载-挠度的相关理论曲线，结果见图6.由图可知，将式(7)和实测的挠度值代入板块平衡法中计算得到的荷载-挠度曲线与试验曲线吻合较好.因此，板块平衡法能准确地计算大挠度下受拉薄膜效应对混凝土双向板承载力的影响.

5 结论

1)大挠度加载时板底产生的裂缝形式与经典屈服线理论假设的模式一致.当板的挠度变形达到L/20时，板均未出现坍塌现象，仍具有较大的承载力.这一变形下对应的混凝土板的承载力远大于经典屈服线理论的计算承载力.

2)利用大尺度试验数据修正了挠度特征值v0和vmax的计算公式.矩形板和方形板的最大挠度值vmax统一取为跨度的1/40;矩形板的v0仍采用原式计算，而对于方形板，则将其系数由0.1修正为0.2.

3)修正后的板块平衡法能准确地计算大挠度下钢筋混凝土板的极限承载力，这为解决混凝土板在极端荷载作用下发生大挠度时的受力分析打下了基础.

表4 试验值与理论值的比较

References)

［1］Bailey C G.Membrane action of unrestrained lightly reinforced concrete slabs at large deflection［J］.Engineering Structures，2001，23(5):470-483.

［2］张先进，李永春，吕曼曼.考虑薄膜效应钢筋混凝土矩形板的极限承载力［J］.武汉理工大学学报，2007，29(6):58-61.Zhang Xianjin，Li Yongchun，Lü Manman.Ultimate bearing capacity of RC rectangular slab considering membrane effects［J］.Journal of Wuhan University of Technology，2007，29(6):58-61.(in Chinese)

［3］Hisham M A，Husain M H，Sarmad S A A.Experimental tests on orthotropically RC rectangular slabs having various restrained edges and subjected to uniform load［J］.Eng ＆ Tech Journal，2009，27(5):913-929.

［4］李国强，张娜思.组合楼板受火薄膜效应试验研究［J］.土木工程学报，2010，43(3):24-31.Li Guoqiang，Zhang Nasi.Experimental study of membrane action of composite floor slabs under fire［J］.China Civil Engineering Journal，2010，43(3):24-31.(in Chinese)

［5］Dong Y.Tensile membrane effects of concrete slabs in fire［J］.Magazine of Concrete Research，2010，62(7):497-505.

［6］Bailey C G，Toh W S.Small-scale concrete slab tests at ambient and elevated temperatures［J］.Engineering Structures，2007，29(10):2775-2791.

［7］Cashell K A，Elghazouli A Y，Izzuddin B A.Failure assessment of lightly reinforced floor slabs［J］.Journal of Structural Engineering，2011，137(9):977-988.

［8］Dong Y L，Fang Y Y.Determination of tensile membrane effects by segment equilibrium［J］.Magazine of Concrete Research，2010，62(1):17-23.

［9］Nilson A H，Darwin D，Dolan C W.Design of concrete structures［M］.13th ed.New York:McGraw-Hill，2004.

［10］中华人民共和国原城乡建设环境保护部.GB 50152—92混凝土结构试验方法标准［S］.北京:中国建筑工业出版社，1992.

［11］全国消防标准化技术委员会建筑构件耐火性能分技术委员会.GB/T 9978—1999建筑构件耐火试验方法［S］.北京:中国建筑工业出版社，1999.