乳腺电阻抗扫描成像数值分析

张 峰 罗立民 鲍旭东 陈北京 张 悦

(1东南大学计算机科学与工程学院，南京210096)

(2西安石油大学计算机学院，西安710065)

(3南京信息工程大学计算机与软件学院，南京210044)

乳腺癌灶组织与正常组织在电导纳参数上具有显著差异，据此已发展出许多相应的乳腺癌检测或诊断技术，如电阻抗断层成像技术、乳房表面电位诊断技术、四电极阻抗测量及电阻抗扫描成像(electrical impedance scanning imaging，EISI)等.EISI检查由于其操作简易、舒适快捷、费用较低等特点，在乳腺癌检测及诊断领域获得了更为广泛的应用.EISI检查过程中，病人呈平躺姿势，固定幅度的低频正弦信号通过病人待检查乳房另一侧手握不锈钢圆柱体(激励电极)引入，临床医师将探头(探头表面虚地)按压在乳房表面采集电流［1］.由于人体胸大肌具有良好的导电特性，可将其看作一等电位面，在胸大肌与探头之间由此建立了一近似平行电场.当乳腺组织中存在癌灶时，由于电导差异，原本呈平行分布的电场将发生扰动，进而使探头检测到的电流分布发生扰动［2］.为了分析电流扰动与测量环境中的哪些因素存在关系，这些因素对于电流扰动的贡献程度大小，从而采取最优的测量设置以凸显电流扰动信息，就需要对成像过程进行相应的分析.

Seo等［2］将 EISI建模为一个半无限空间，通过边界元方法仿真了乳房中存在癌灶的成像特点，初步指出电流扰动与癌灶深度存在密切关系.由于模型未涉及乳房实际大小和探头实际结构，因此未能反映成像过程中的边界效应问题.Scholz等［3］将成像过程建模为一个单一的体积导体问题，结合有限元分析方法对成像过程进行了初步的仿真分析.指出电流扰动受癌灶深度、大小以及乳房大小等因素影响，但未对上述因素对于电流扰动程度的重要性进行分析.需要指出的是，Scholz等的成像模型存在不足:①将乳房等效为单一组织，与实际情况不符.②将胸大肌所在的等电位面看作与探头表面同等大小，在一定程度上降低了边界效应的影响.实际上胸大肌所在的等电位面与乳房大小一致，大于探头表面.③将探头表面理想化处理，将其看作一个理想的零电位面，未考虑电极间隔处的边界条件.

本文结合女性乳房结构特点、乳房组织电参数测量结果、中国女性乳房大小以及EISI探头结构，构造了一个更加接近EISI实际的乳房成像模型;通过COMSOL有限元仿真软件对模型的控制方程——拉普拉斯方程进行求解，进而获得乳房表面的电流分布.通过Yates算法进一步分析了成像过程中的相关参数对于电流扰动的贡献程度，为进一步通过控制成像过程中的相关参数以提高EISI检测乳腺癌的性能提供理论指导.

1 方法

1.1 理论基础

人体组织的电参数特性可以看作如下所示的电导纳形式:

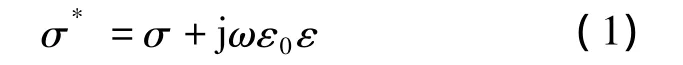
式中，σ为电导;ε0为真空中的介电常数，其大小为8.85×10－12F/m;ε 为相对介电常数;ω =2πf为测量信号角频率，f为测量信号频率.

EISI检测过程通过给乳房组织施加低频正弦激励(激励频率小于20 kHz)，然后在乳房表面检测电流.考虑到乳房内部无电流源，同时不存在电流累积效应，因此乳房内部的电位分布满足典型的拉普拉斯方程:

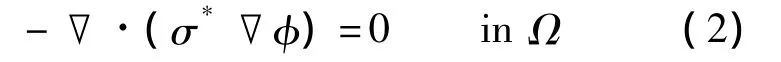
式中，Ω代表待检测的乳房;φ为乳房内及表面的电位值.EISI检测过程中正弦激励电压由患者手握的电极棒引入并直达胸大肌(具有良好的导电特性)，然后经过乳房组织由乳房表面的探头电极(电极均虚地)流出.因此，电位分布除满足式(2)的控制方程以外，还需满足如下所示的狄利克莱边界条件:

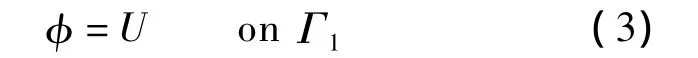
狄利克莱边界Γ1包括探头表面(即电极表面和保护电极表面)和胸大肌所在平面，其边界条件分别为U=0 V和U=1.9 V(EISI激励电压幅度).除边界Γ1外，Ω的其他表面统称为纽曼边界Γ2.Γ2边界所接触的外围物质为空气，考虑到皮肤的电导远大于空气，因此在该边界不存在边界电流.即式(2)所描述的电场分布还需满足如下所示的纽曼边界条件(即电隔离条件)［4］:

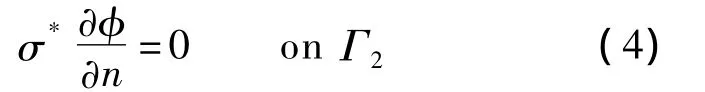
通过求解式(2)～(4)，可获得EISI的电位分布φ.在探头表面，考虑到电极可看作理想导体，则其可看作等位体，其电场强度切向分量为零.所以，在探头与乳房的接触面上，组织中的电场强度仅有法向分量［5］.对电位φ按下式即可计算出电极表面的电流密度分布:

获得电极表面电流密度之后，对下式进行积分可获得探头检测的电流分布:

当测量频率低于100 kHz，人体组织中的传导电流远大于位移电流，因此电介效应可以忽略.EISI测量频率范围为0.2～20 kHz，因此在后续仿真中对组织电参数仅考虑电导值［6］.

1.2 仿真方法

女性乳房由乳腺组织和表面皮肤组成.乳腺组织由腺体以及脂肪等组成，年轻女性乳房致密，乳腺组织以腺体为主;随着年龄增长，腺体逐渐退化，乳腺组织逐渐以脂肪为主.我国妇女乳房大小分布区间为100～170 mm［7］，平躺姿态乳房厚度在30～60 mm 之间［8］.乳房皮肤平均厚度为 5 mm，电导率为 0.01 S/m［4］.EISI检测过程中，乳房经医师按压抹平之后检测，因此可近似看作一方形柱状体，其边长为100～170 mm，厚度为30～60 mm.该柱状体为2层结构，表面为皮肤层.图1为一计算示例.图1(a)是直径为100 mm的乳房EISI检测模型，乳腺厚度50 mm(包括皮肤厚度5 mm)，乳腺组织中存在一半径为10 mm的癌灶，其深度为20 mm;癌灶组织电导率为0.7 S/m，乳腺组织为脂肪，电导率为0.04 S/m.图1(b)为采用四面体单元处理后的模型，图1(c)为探头所在表面局部放大效果.求解式(2)～(5)，可得探头所在表面的电流密度分布，如图1(d)所示.为了减少由于乳房大于探头所带来的电流扰动信息干扰探头外侧的测量电极，探头设计中在测量电极(呈正方形，边长3 mm，相互间隔1 mm)四周设计了保护电极，在一定程度上减少了边界效应对于探头边缘的测量电极的干扰，有利于突出癌灶与周围正常组织电导差异所引入的电流扰动信息.由图1(d)可看出，保护电极所在位置电流密度明显大于测量电极，有效地避免了边界效应带来的电流扰动对测量电极的影响.对于图1(d)所示的电流密度分布，根据式(6)对每一测量电极进行表面积分，可以得到每个测量电极的电流大小.将8×8电极测量得到的电流按照其对应位置显示，即可得到探头的电流分布.

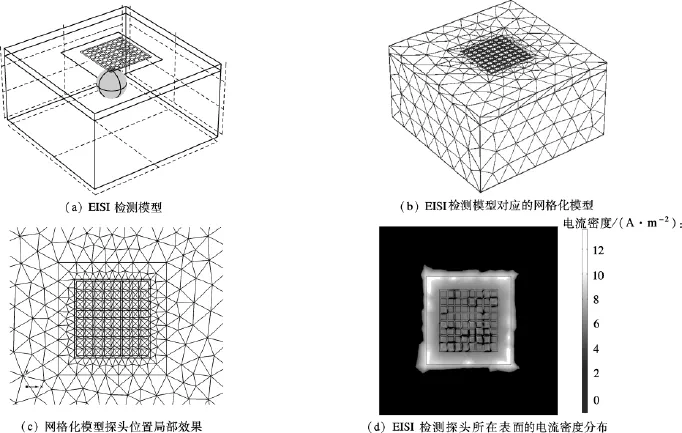
图1 EISI仿真分析模型

如果乳房大小与探头尺寸相等，那么激励面(胸大肌平面，见图1(a))与探头面大小完全相等，电流只能在这2个平面之间流动，因此边缘扰动(边界效应)几乎可以忽略.图2(a)为此种情况下的探头表面电流分布，可见明显的由癌灶所带来的电流扰动信息.与之相比，图1(a)由于乳房尺寸大于探头，因此由胸大肌平面出发的部分电流会穿出探头所在的柱状体，然后在接近探头面过程中逐渐汇拢，最终由探头边缘(主要为保护电极，其次为外围的测量电极)流出，由此导致外围测量电极的电流增大(见图2(b))，抵消了癌灶所带来的扰动信息，减小了图像对比度.图2(c)、(d)为进一步增大乳房尺寸后探头检测得到的电流分布.可见边缘扰动更加明显，由癌灶带来的扰动信息有逐渐被淹没的趋势.为了尽可能突出癌灶所带来的扰动信息，下面将进一步分析成像模型中的相应参数对突出癌灶信息的贡献.为了客观地评价各个参数的效应，本文定义了一个癌灶显著性评价指标(breast cancer significance measure，BCSM):

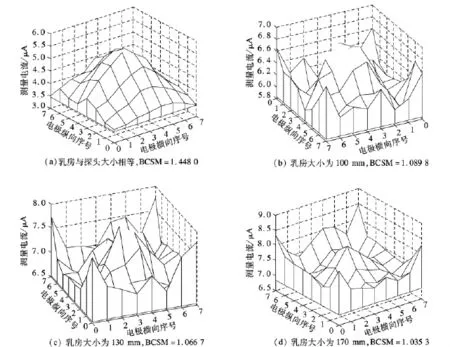
图2 不同尺寸的乳房表面检测得到的电流分布

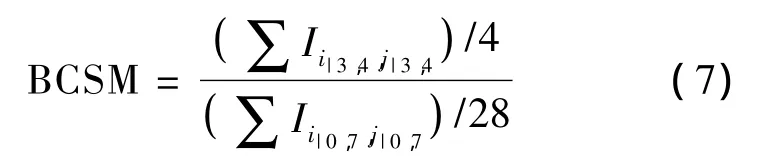
BCSM表示探头中心位置的4个电极检测电流的平均值与探头最外围4个边的28个电极检测电流的平均值之比.BCSM＞1，表示癌灶带来的扰动信息有可能在检测过程中被识别;BCSM＜1，则表示癌灶带来的扰动信息淹没于边界效应，扰动信息很难被识别.

2 结果

结合EISI乳房模型，根据文献［7-8］确定了模型中相关参数的数值范围(见表1).其中，癌灶大小的设置参考文献［4］，癌灶深度的设置取决于EISI的临床检测深度(EISI检测深度一般在3 cm以内)，因此本文将癌灶半径设为2.5～10 mm，深度设为15～25 mm进行仿真分析.乳腺组织由腺体和脂肪等组成，脂肪的电导率为0.04 S/m，乳腺腺体的电导率为0.5 S/m，因此乳腺组织的电导率应该处于0.04～0.5 S/m之间.根据表1的参数设置，结合每个因素2个水平设置，进行了25=32组仿真实验.针对每组实验，计算其探头检测电流分布的BCSM指标，具体仿真结果见表2.表2第1列给出了每一组实验的参数设置情况，其中(1)表示5个参数均处于其参数范围的低水平.对于其余31个用字母表示的参数组合(a，b，ab，…)，凡是组合中出现的字符表示该因素处于高水平，其余未出现的字符所代表的因素均处于低水平.如ab表示这组实验的参数设置情况为:癌灶深度25 mm，半径10 mm;乳房厚度30 mm，直径100 mm，乳腺组织电导率0.04 S/m.对多个因素进行效应分析，通常采取正交表分析方法.但是，正交表分析方法虽然简单，但非常繁琐，容易出错.为此，本文采取Yates算法来进行多因素效应分析［5］.

Yates算法的分析结果如表2所示.3个因素及以上的组合效应作为误差进行分析.以5%的显著性水平分析，F0.05;1，32=4.17.由表 2 中的 F 值可见，D ×E(D 和E因素交互作用)，B，B×E，A，A×B及 A×E等因素(按显著性水平降序排列)显著影响探头电流分布图像的BCSM值，即这些因素显著影响癌灶所引入的电流扰动是否能够被有效识别.但这些因素处于何种设置更有利于癌灶被识别还需进一步分析.以D×E复合效应分析为例，D1×E1测量(表示因素D和E均处于高水平)得到的 8个 BMSC 为 0.958 4，0.975 1，0.970 4，0.962 0，0.927 6，0.978 3，0.922 6，0.923 0，平均值为0.952 2;D0× E1测量得到的 8个 BMSC 为0.973 6，0.968 7，0.988 7，0.968 5，0.951 2，0.945 6，0.985 7，0.950 0，平均值为0.966 5;D0×E0测量得到的8个BMSC 为0.845 5，0.833 3，1.472 7，0.992 3，0.819 9，0.806 0，1.907 2，0.920 2，平均值为1.074 6;D1×E0测量得到的8 个 BMSC 为0.774 0，0.765 1，1.849 6，0.909 3，0.785 1，0.779 6，1.740 4，0.869 0，平均值为1.059 0.可见 D0×E0设置的 BCSM 数值最大，即乳房直径越小，乳腺组织电导率越小越有利于突出癌灶信息.B0(癌灶半径为2.5 mm)测量得到16个BMSC值，其平均值为0.876 6;B1(癌灶半径为10 mm)测量得到16个BMSC值，其平均值为1.149 6.B0×E0的BCSM 平均值为0.801 1;B1×E0的BCSM 平均值为1.332 6;B0×E1的BCSM 平均值为0.952 1;B1×E1的BCSM 平均值为0.966 5.A0的 BCSM 平均值为 1.120 7;A1的 BCSM 平均值为0.905 4.A0×B0的BCSM 平均值为0.879 3;A1×B0的 BCSM 平均值为0.873 9;A0×B1的BCSM 平均值为1.362 2;A1×B1的 BCSM平均值为0.936 9.A0×E0的 BCSM 平均值为1.274 3;A1×E0的 BCSM 平均值为 0.859 4;A0×E1的BCSM 平均值为0.967 2;A1×E1的 BCSM平均值为0.951 5.综上分析，乳房直径越小，癌灶半径越大，深度越浅，乳腺组织电导率越小，由癌灶所引入的电流扰动越明显.

表1 EISI检测过程乳房模型相应参数范围

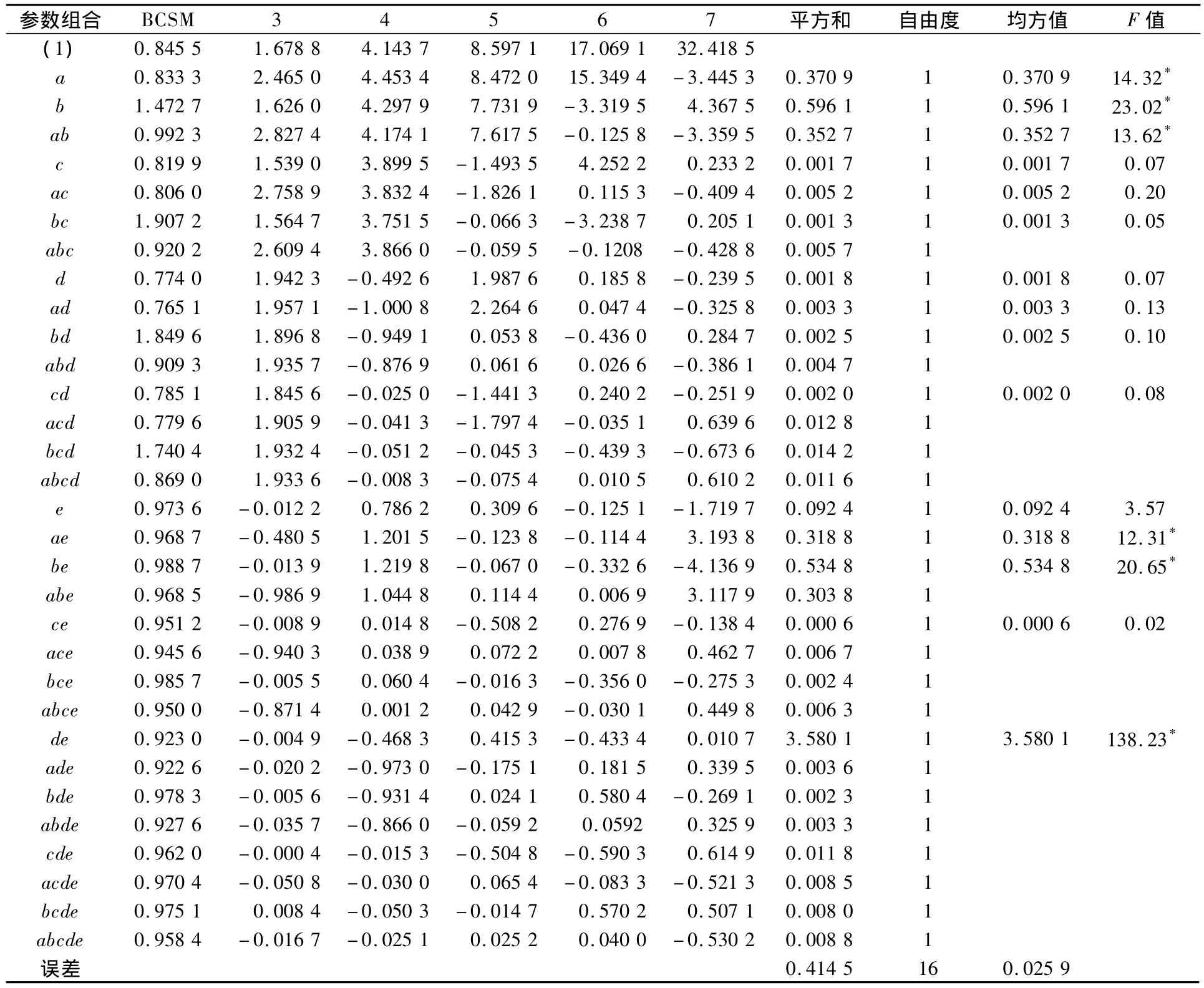
表2 Yates算法分析结果

3 讨论

通过对不同参数进行水平组合，并采用Yates算法进行方差分析，发现乳房大小、癌灶大小和深度以及乳腺组织成分(涉及电导率)都直接影响癌灶信息是否能够在乳房表面电流分布中被体现.乳腺组织成分影响BCSM数值大小的原因，可能与癌灶和组织的电导比有关.文献［9］的理论分析表明，癌灶扰动的程度与(σ－1)/(σ+2)呈正比关系，其中σ为癌灶与周围组织的电导比.对癌灶大小的分析表明，癌灶越大越有利于癌灶检出.但必须说明的是，本文中仿真的癌灶半径最大为10 mm.如果癌灶更大，反而可能导致其不易检出.假设癌灶半径大于20 mm，其已大于探头测量电极区域大小，探头所有电极的测量电流整体增加，无法体现局部电流扰动.为了提高EISI检测性能 (即提高BMSC数值)，未来的研究方向可以集中在以下方面:设计适当的测量夹具，控制乳房大小以及厚度［10］(减小厚度自然能够减少癌灶深度)以提高癌灶检出能力;改进探头设计，在确保探头与乳房表面可靠接触的前提下，增大保护电极或测量电极数目［11］(增加有效测量电极数目)以减少边界效应影响，同时避免大尺寸癌灶漏检的发生.

4 结语

基于EISI乳腺癌检测模型，采用有限元分析方法进行仿真计算，并结合Yates算法进行多因素分析.结果表明，乳房大小、癌灶大小、深度以及乳腺组织成分因素显著影响乳腺癌的检出.乳房越小，癌灶尺寸(在一定范围内)越大，深度越浅，乳腺组织电导率越小，由癌灶引起的乳房表面电流扰动越大.下一步计划采取适当手段减少乳房大小、厚度以及改进探头设计，进一步提高EISI的乳腺癌检测性能.

References)

［1］Assenheimer M，Moskovitz O L，Malonek D，et al.The T-SCAN technology:electrical impedance as a diagnostic tool for breast cancer detection［J］.Physiological Measurement，2001，22(1):1-8.

［2］Seo J K，Kwon O，Ammari H，et al.A mathematical model for breast cancer lesion estimation:electrical impedance technique using TS2000 commercial system［J］.IEEE Transactions on Biomedical Engineering，2004，51(11):1898-1906.

［3］Scholz B，Anderson R.On electrical impedance scanning—principles and simulations［J］.Electromedica，2000，68:35-44.

［4］Ng E Y K，Ng W K.Parametric study of the biopotential equation for breast tumour identification using ANOVA and Taguchi method［J］.Medical＆Biological Engineering ＆Computing，2006，44(1/2):131-139.

［5］张峰，罗立民，鲍旭东.基于电阻抗扫描成像的乳腺癌自动诊断及参数提取［J］.自动化学报，2012，38(5):850-857.Zhang Feng，Luo Limin，Bao Xudong.Automatic diagnosis and complete parameters extraction algorithm for breast carcinoma based on electrical impedance scanning［J］.Acta Automatica Sinica，2012，38(5):850-857.(in Chinese)

［6］Zou Yongning.Simulation and development of a dualface electrical impedance imaging technique with applications to breast cancer detection［D］.Washington:George Washington University，2003.

［7］田燕，訾绍霞，俞士珍，等.中国健康成年女性正常乳房的生理测量［J］.中国美容医学，2004，13(5):524-526.Tian Yan，Zi Shaoxia，Yu Shizhen，et al.Physiological measurement of breast of Chinese normal women［J］.Chinese Journal of Aesthetic Medicine，2004，13(5):524-526.(in Chinese)

［8］吴琦，何之彦，罗树春，等.中国女性仰卧位乳房厚度测量及临床意义［J］.医学科技，2003(1):36-37.Wu Qi，He Zhiyan，Luo Shuchun，et al.Breast thickness measurement of Chinese women in the supine position and clinic applications［J］.Medical Science ＆Technology，2003(1):36-37.(in Chinese)

［9］张峰，罗立民，鲍旭东.基于电阻抗扫描成像的乳腺癌检测方法［J］.东南大学学报:自然科学版，2012，42(1):45-49.Zhang Feng，Luo Limin，Bao Xudong.Method for detecting breast cancer by electrical impedance scanning［J］.Journal of Southeast University:Natural Science Edition，2012，42(1):45-49.(in Chinese)

［10］Kao T J.A 3-D reconstruction algorithm for electrical impedance tomography using planar electrode arrays［D］.Troy:Rensselaer Polytechnic Institute，2005.

［11］Zhao Mingkang，Liu Qin，Oh T I，et al.Development of a trans-admittance mammography(TAM)using 60×60 electrode array［J］.Journal of Physics:Conference Series，2010，224(1):012045.