考虑侧斜及纵倾情况下的船舶螺旋桨最佳环量分布计算
王超,何苗,周剑,熊鹰,黄胜
(1.海军工程大学 船舶与动力学院,湖北武汉430033;2.哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001)
船舶螺旋桨的径向环量分布直接决定了螺旋桨的载荷分布及效率,因此,如何计算螺旋桨最佳环量分布是船舶螺旋桨理论设计及性能预报中重要的一步.Betz[1]早在1919年就以升力线理论为基础导出了均匀流中螺旋桨最佳环量分布的条件,Lerbs[2]也提出了一种计算最佳环量分布的方法,并将其应用于非均匀流中的螺旋桨.他们都用了Betz条件,但其方法只对于均匀流的情况是完全正确的.初始的升力线理论没有考虑螺旋桨的侧斜分布与纵倾分布,而且Lerbs提出的诱导因子法并没有考虑附着涡以及侧斜分布等产生的影响.
本文应用螺旋桨的升力线旋涡模型[3],把集中的附着涡放置在桨叶的中线即弦长中点处,以计及桨叶侧斜和纵倾的影响,如果桨叶没有侧斜和纵倾,则升力线仍为径向线,否则升力线为一空间曲线.通过计算分析了侧斜及纵倾变化对螺旋桨最佳环量分布、诱导速度以及对水动力螺距角的影响等.
1 升力线基本理论
升力线上的诱导速度采用离散马蹄涡模型,即把升力线均匀离散为M个附着涡段,形成M个螺旋马蹄形涡.记涡段端点的径向坐标为rom(m=1,M+1),涡段中点径向坐标为rm(m=1,M),则马蹄涡系在控制点处产生的诱导速度可按下式[4]计算:

式中:Γn为第 n 个马蹄涡的环量强度,Ha,t(m,n)为第n个单位强度的螺旋马蹄形涡所产生的诱导速度,下标a和t分别为轴向和切向方向.
螺旋桨工作时,尾流具有诱导速度而产生诱导损失,此种能量损失等于螺旋桨所吸收的功减去螺旋桨所作的有用功,令Ei表示单位时间内能量损失[5],则

为了便于讨论,给定Ti,此时Ei取极小值时,Qi必最小.因此,船舶螺旋桨的最佳环量分布条件可描述为:在给定推力(或转矩)的情况下,使螺旋桨效率最高,即螺旋桨的转矩最小(或推力最大),由此得到的环量分布称为最佳环量分布.这里,螺旋桨的尾涡忽略径向收缩,且忽略粘性力.则螺旋桨的无粘推力及转矩可表示为[6]
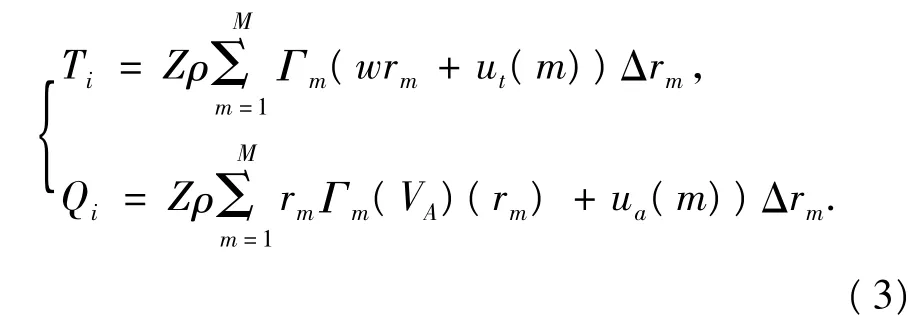
2 计入纵倾与侧斜的螺旋桨最佳环量分布的计算
考虑了螺旋桨的侧斜分布后,升力线模型中的附着涡线不再是沿着径向的一条直线段,因此,在求解螺旋桨诱导速度时不可再直接应用Lerbs诱导因子法.本文采用离散涡分布的方法,为了方便讨论,忽略流体粘性,假定推力已知,使螺旋桨的转矩最小.求解过程中主要采用了以下2种计算方法.
1)方法A
即拉格朗日乘子法求极小值的方法[4],为此引入函数 F(λ,Γ1,Γ2,…,ΓM)=Qi+ λ[Ti(1-t)-T],此问题即为求函数F的极小值.于是令

通过上式可得出线性方程组:
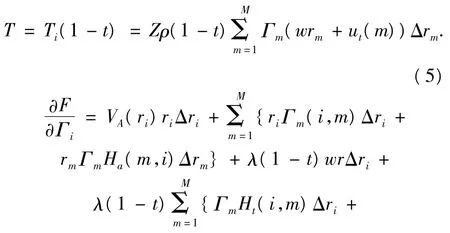

式(5)及(6)构成了M+1个线性方程,为了使方程系数比较工整,往往首先给定定拉格朗日乘数λ的初值,这样方程(6)就变成了含有M个未知环量的M个线性方程组:

先计算出推力,如果推力不等于给定的推力,则修改拉格朗日乘数λ,进行下一次迭代,直到推力等于给定的推力为止,此时得到的环量分布即为最佳环量分布[6].但由于诱导速度 ua、ut与水动力螺距βi有如下关系:

而初始时βi(j)往往未知,通常以各半径处的进角为初始迭代值.
2)方法B
由前面推导的螺旋桨最佳环量分布条件,建立确定最佳环量分布的线性方程组进行数值计算[3].以敞水螺旋桨为例.假定螺旋桨推力为T,直径D,桨叶数Z,进速为VA,桨叶上诱导速度为ua、ut.
敞水条件下最佳环量分布条件为

式中:C为常数.
由叶元体的速度多角形可知:
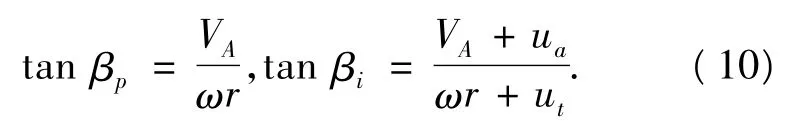
将式(10)代入式(9),并结合式(1)可得以下线性方程组:

考虑到影响系数Ha,t(i,j)与螺旋桨水动力螺距角有关,而初始水动力螺距角是未知的,通常以螺旋桨进角作为初始迭代值,迭代公式见式(8).
由线性方程组可知,常数C的取值直接关系到环量分布的大小.为了快速得到给定推力T的螺旋桨最佳环量分布.通常先根据螺旋桨直径D与推力T计算理想推进器的推进效率ηiA:
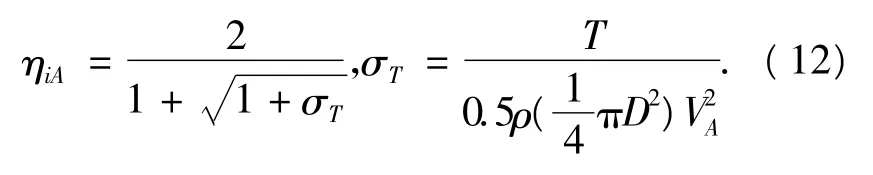
令 C=0.95ηiA,代入方程组(11),可求得螺旋桨敞水最佳环量分布,修改常数C可得给定推力下的螺旋桨最佳环量分布.若考虑螺旋桨船后及推力减额的影响,可令再代入方程组(11),由水动力螺距角的迭代公式(8)、修改常数C及求解方程组(11)便可得螺旋桨的最佳环量分布.
3 计算结果分析
3.1 角度步长对螺旋桨最佳环量分布的影响
因为诱导速度的计算直接关系到了螺旋桨最佳环量分布的计算,而诱导速度与影响系数Ha,t(m,n)有着直接关系.在计算 Ha,t(m,n)时,自由涡系部分计算是直接根据自由涡系诱导速度的积分公式进行数值计算的,所以角度步长的选择对Ha,t(m,n)及螺旋桨最佳环量分布影响很大[8].计算所采用的螺旋桨参数如表 1[9].

表1 螺旋桨主要参数Table 1 Main parameters of propeller
由图1可以得出角度步长DAF取得过大时,最佳环量分布偏差较大[10],这是因为角度步长过大时,自由涡线形状与真实螺旋线偏差较大;角度步长取得过小时,计算精度可以满足要求,但计算时间大大加大,不利于快速计算.而取DAF=2.5度时,最佳环量分布基本上趋于稳定,因此,下文计算时角度步长均取为DAF=2.5度.
3.2 纵倾的影响
采用方法 B 分别对纵倾为 0°、1°、2°、…7°、8°的无侧斜螺旋桨最佳环量进行了计算与对比;同时计算分析了纵倾对螺旋桨诱导速度与水动力螺距角的影响,详细可见图2~5(实体标志曲线位于左侧坐标之中).

图1 敞水情况下最佳环量分布曲线Fig.1 The optimal circulation distribution in open water condition
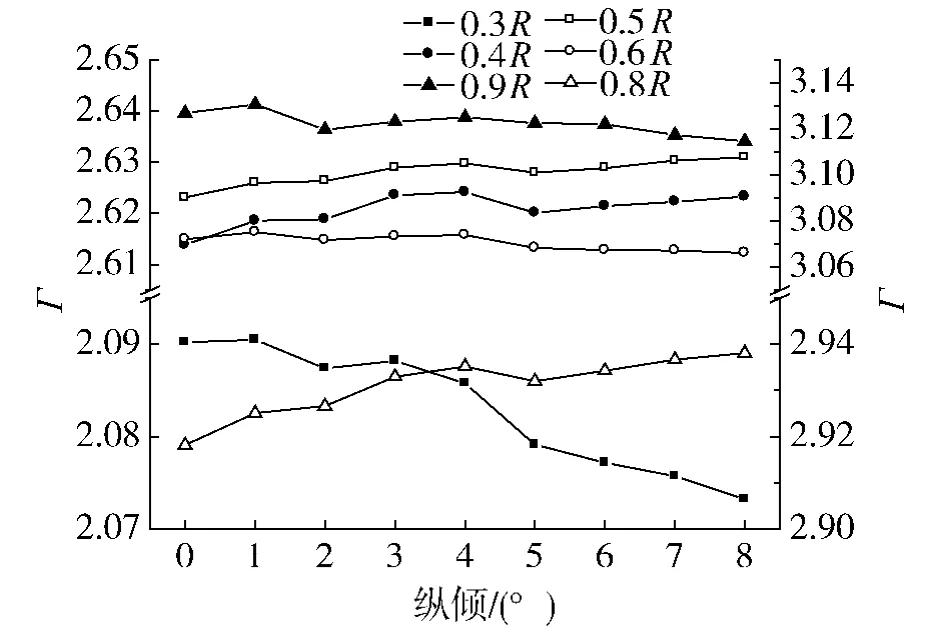
图2 不同半径处环量随纵倾变化曲线Fig.2 The change of optimal circulation distribution along with rake increasing
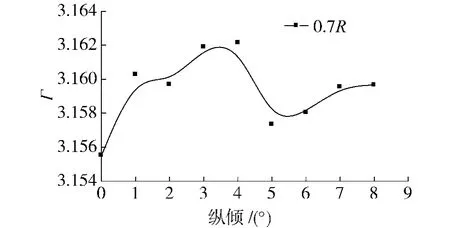
图3 最佳环量分布最大值随纵倾变化曲线Fig.3 The max value of optimal circulation distribution along with rake changing
由图2可知,在靠近叶根与叶梢处最佳环量随着纵倾增加呈现减小的趋势,而在其他半径处则呈现相反的规律.同时,由图3可以看出最佳环量分布的最大值随纵倾变化幅度较小,但均比无纵倾时要偏大些(计算中最大值位于0.7R处).


图4 不同纵倾情况下的诱导速度Fig.4 The induce velocity in different rake conditions
由图4可知,随着纵倾增加,轴向诱导速度Ua与切向诱导速度Ut均逐渐减小.但由于理论上自由涡线是一条半无无穷长的近似螺旋涡线,计算时并未完全计及,因此,在外半径区内切向诱导速度Ut本身已经很小了,容易出现一些误差.
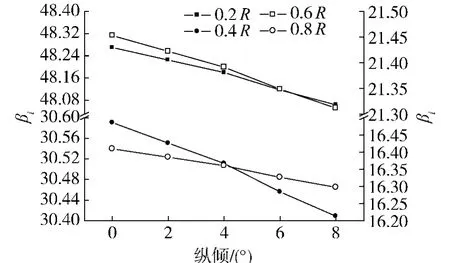
图5 各个半径处水动力螺距角随纵倾变化曲线Fig.5 The change of βialong with rake increasing
由图5(实体标志曲线位于左侧坐标之中)可明显观察到,随着纵倾的增加,螺旋桨各个半径处的水动力螺距角均呈现递减的趋势,在螺旋桨的几何螺距角一定的情况下,螺旋桨各个半径剖面处有效攻角则相应增加,这在某一程度上说明了增加纵倾可以提高螺旋桨推力系数,但从图5中可看出,水动力螺距角的变化不是很大,故影响很小.
3.3 侧斜的影响
为了考虑侧斜分布对敞水及船后螺旋桨最佳环量分布的影响,采用方法A分别计算敞水及船后的有无侧斜情况下螺旋桨最佳环量分布.计算采用的螺旋桨的主要特征参数如表2[11],伴流及侧斜分布见表3.
由图6可知,在敞水或伴流情况,侧斜分布使螺旋桨最佳环量分布在内半径区有所增加,而且在一定范围内随着侧斜角的增加环量呈现增大的趋势,但总的影响不是很大.而由图7和图8可知,侧斜分布对轴向诱导速度的影响较切向诱导速度偏大,而且轴向诱导速度随着侧斜分布的变化与切向诱导速度成相反的趋势.

表2 螺旋桨主要参数Table 2 Main parameters of the propeller

表3 伴流分布及侧斜分布Table 3 Wake flow and skew conditions

图6 敞水及船后伴流螺旋桨最佳环量分布Fig.6 The optimal circulation distribution under open water and wake flow conditions

图7 轴向诱导速度Ua径向分布Fig.7 The radial distribution of Ua

图8 切向诱导速度Ut径向分布Fig.8 The radial distribution of Ut
由图9(实体标志曲线位于左侧坐标之中)可知,不论在敞水或伴流情况下,随着侧斜角的增加,内半径区内的水动力螺距角呈现增大的趋势,而在外半径区的水动力螺距角则呈现减小的趋势,这是因为侧斜分布对轴向诱导速度的影响与切向诱导速度的影响相反的缘故.

图9 不同侧斜分布的水动力螺距角Fig.9 The βiof different skew distributions
4 结论
该文针对传统升力线理论的特点,计入纵倾与侧斜的影响,根据编写的程序求解了螺旋桨的最佳环量分布,重点分析纵倾与侧斜对螺旋桨最佳环量分布等的影响.通过计算分析得出以下结论:
1)通过计算分析,获知采用角度步长DAF=2.5度可以得出比较可靠的结果.
2)随着纵倾增加,在靠近叶根与叶梢处的最佳环量呈现减小的趋势,而在其他半径处则呈现相反的规律;同时随着纵倾增加,轴向诱导速度与切向诱导速度以及螺旋桨各个半径处的水动力螺距角均逐渐减小.
3)侧斜分布对轴向诱导速度的影响与切向诱导速度的影响相反,从而随着侧斜角的增加,内半径区内的水动力螺距角呈现增大的趋势,而在外半径区的水动力螺距角则呈现减小的趋势.
[1]王国强,董世汤.船舶螺旋桨理论与应用[M].哈尔滨:哈尔滨工程大学出版社,1985:42.
[2]LERBS H.Moderately loaded propellers with finite number of blades and an arbitrary distribution of circulation[J].Trans The Society of Naval Architects and Marine Engineering,1952,60:73-123.
[3]苏玉民,黄胜.船舶螺旋桨理论[M].哈尔滨:哈尔滨工程大学出版社,2003:45-47.
[4]谭廷寿,熊鹰.基于B样条的螺旋桨升力面设计[J].海军工程大学学报,2005,17(6):37-42.TAN Tingshou,XIONG Ying.Propeller design by lifting surface theory based on B-spline[J].Journal of Naval University of Engineering,2005,17(6):37-42.
[5]盛振邦,刘应中.船舶原理(下册)[M].上海:上海交通大学出版社,2004:22.
[6]吴光林,严谨.船用螺旋桨理论研究的发展与方向[J].中国舰船研究,2009,4(1):8-12.WU Guanglin,YAN Jin.Development and methods on theoretical research of marine propellers[J].Chinese Journal of Ship Research,2009,4(1):8-12.
[7]CONEY W.Optimum circulation distributions for a class of marine propulsors[J].J Ship Res,1992,36(3):210-222.
[8]杨国伟,何植岱.计及尾涡收缩的螺旋桨滑流计算[J].空气动力学学报,1995,13(1):83-86.YANG Guowei,HE Zhidai.Flow-field calculation of propeller slipstream about vortex contraction[J].Acta Aerodynamic Sinica,1995,13(1):83-86.
[9]王言英,张忠业,华汉金.螺旋桨理论设计与实验研究[C]//第二届船舶推进器及空泡学术讨论会.[s.l.],1983:63-64.
[10]覃新川,黄胜,常欣.计入尾涡衰减影响的船舶螺旋桨扰动场数值分析[J].哈尔滨工程大学学报,2007,28(8):847-851.QIN Xinchuan,HUANG Sheng,CHANG Xin.Numerical calculation of a ship propeller's wake with attenuation[J].Journal of Harbin Engineering University,2007,28(8):847-851.
[11]谭廷寿.非均匀流场中螺旋桨性能预报和理论设计研究[D].武汉:武汉理工大学,2003:43.TAN Tingshou.Performance prediction and theoretical design research on propeller in non-uniform flow[D],Wuhan:Wuhan University of Technology,2003:43.

