基于期望模式修正方法的混合网格多模型估计

刘扬，国强，吴钦章

(1.中国科学院光电技术研究所，四川成都610209;2.中国科学院研究生院，北京100049;3.哈尔滨工程大学 信息与通信工程学院，黑龙江哈尔滨150001)

变结构多模型算法(VSMM)［1］是近年来发展起来的一种有效的机动目标跟踪算法，它克服了交互多模型(IMM)算法的缺陷，费效比IMM算法高，在运算量及其实现的复杂度与跟踪性能之间达到了较好的平衡，因此，近年来受到越来越多的关注.VSMM算法的技术核心是模型集合自适应(MSA)策略.MSA策略用于确定每一个时刻参与状态估计的有效模型集.目前已经提出的MSA策略包括模型集切换(MGS)［2］、可能模型集(LMS)［3］、期望模式修正(EMA)［4］等算法.其中EMA算法发展较为成熟，应用较为广泛.本文以该算法为基础，分析EMA算法存在的局限性，同时引入可能模型集(LMS)技术和自适应网格(AG)技术，实时产生一个混合模型网格，最后利用最优融合原理得到系统的整体估计.

1 EMA算法及其局限性

EMA算法的基本思想是:首先设定一个相对较大且结构固定的模型集M来覆盖整个系统模式空间，同时利用固定模型集M的滤波结果，实时产生一个与系统真实模式更为匹配的修正模型C，并利用修正模型C再次对机动目标进行滤波估计，最后利用最优融合原理得到系统的整体估计，从而达到利用修正模型C对固定模型集M的滤波结果进行修正的目的.

EMA算法中的固定模型集M所包含的模型在一个连续模式(加速度)空间S内均匀分布，每一个模型被看作模式空间中的一个点，具有不同的加速度，而模型间的双向箭头表示从一个模型到另一个模型的跳变，如图1(a)所示.修正模型C可以位于模式空间中的任何位置，该位置由固定模型集M的滤波结果实时决定.通常修正模型C是模型集M滤波结果的概率加权和:

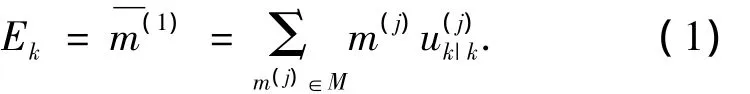
k时刻，EMA算法所利用的模型集如图1(b)所示，目标实际的机动加速度在“*”处.理想状况下，根据固定模型集M在k时刻的滤波结果所产生的修正模型C位于“*”附近，相对于模型集M中的模型，模型C更加接近于系统的真实模式.因此模型C能够对固定模型集M的滤波结果起到修正作用.

图1 EMA算法模型集拓扑结构Fig.1 The topology of the model set in EMA

EMA算法的一个运行周期如下:

1)在时刻 K 基于模型集 Mf=Mk－1－ Ek－1运行VSMM 算法一个递归周期 VSMM［Mf，Mk－1］获得模型的状态估计、估计误差协方差以及模型概率{，

2)利用式(1)得到期望扩张模型C.

3)运行递归 VSMM［C，Mk－1］获得状态估计，估计误差协方差以及模型概率

4)运行融合估计 EF［Mf，C;Mk－1］一个周期得到属于模型集Mk=Mf∪C的整体估计，误差协方差以及模型概率

上述EMA算法存在以下几个不足:

1)修正模型C对模型集合M具有很强的依赖性，但是由于模型集合M是一个固定结构的模型集，当机动目标发生机动时，模型集M的估计结果会偏离目标，这就导致在此基础上得到的修正模型C与系统的真实模式之间存在偏差，如图1(c)所示.此时，模型C很难对固定模型集M的滤波结果起到修正作用，从而影响算法的估计精度.

2)由于模型集M具有固定结构，因此，算法滤波结果对集合拓扑结构具有很大的依赖性.同时，由于模型集合M必须完全覆盖整个系统模式空间，导致包含的模型数量较多，模型数量过多容易引起模型间不必要的竞争.

3)修正模型C作为单独的修正模型，其修正能力是有限的.

2 改进的期望模式修正(M-EMA)算法

2.1 算法思想

M-EMA算法利用2个独立模型网格组成当前参与估计的模型集:基础网格M和修正网格C.2个网格分别以各自不同的时间精度和空间精度进行状态估计.k时刻的网格M和网格C仅仅由k－1时刻的网格M和网格C来决定.这就消除了EMA算法中修正模型C对固定模型集M的依赖.同时引入自适应网格(AG)技术，利用该技术操作简单实现快速的特点，在采样间隔较短，模型间距较小的高分辨率环境下，根据目标的实际机动实时产生一个自由滑动的修正模型网格C用来替代EMA算法中单个的修正模型C从而使模型网格C的修正力度加强.然后引入可能模型集(LMS)技术应用于基础网格M的产生，使基础网格M成为能够根据目标机动情况实时变化的模型集，削弱EMA中模型集M对目标机动方式和模型集拓扑结构的影响;并且减少了那些与系统模式相距较远的模型，使得模型的分布更加集中.

2.2 算法实现

根据M-EMA算法思想可知，M-EMA算法的关键是如何根据目标机动的实际情况得到基础网格M和修正网格C.

M-EMA在确定基础模型网格M时，利用LMS方法，将所有模型分为不可能模型集、有效模型集和重要模型集3类.模型集自适应方法为:1)删除不可能模型集;2)保留有效模型集;3)激活与重要模型毗邻的模型集.

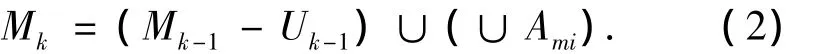
式中:Mk－1为k－1时刻所使用的模型集;Mk为k时刻应该使用的模型集;Uk－1分别为 Mk－1中不可能模型和重要模型的集合;Ami为与重要模型毗邻的模型集.由此基础模型网格M便成为一个根据目标机动情况实时产生、模型分布相对集中、模型数量相对较少的变结构模型集，算法详细流程参考文献［3］.

修正模型网格C的确定则利用AG技术，网格C中各个模型的参数在一个连续区域内自适应的滑动.因此任何时刻只需要少量与系统模式相关的模型.假设选择5个匀加速模型组成该修正网格，各个模型的加速度参数对应于不同机动水平的网格点，记为 C={CCen，CTop，CDow，CLef，CRig}，其中 CCen为网格中心，{CTop，CDow，CLef，CRig}分别是上、下、左、右4个方向上的网格点.修正模型网格C的确定分为2个主要步骤:步骤1用于更新中心模型CCen;步骤2用于实现4个方向上的网格点的更新.文献［5］中详细描述了自适应网格的产生，但文献［5］中的模型网格仅仅在水平方向进行自适应，这里将文献［5］中水平方向的自适应方法扩展到竖直方向，从而产生修正模型网格C.同时在参考文献［6］中的改进方法，引入平滑因子α，提高修正网格C的稳定度.由此，修正网格C摆脱了对模型集M的依赖，同时由于C在时间和空间上分辨率相对较高，因此更利于接近系统的真实模式，实现对基础网格M的有力修正.

在得到上述基础网格M和修正网格C之后，利用最优融合原理得到系统的整体估计.M-EMA算法中参与融合的模型集合拓扑结构如图2所示，“*”处表示系统真实模式，图2(a)、(b)描述了修正网格C在k和k+1时刻在系统模式空间中的位置，正方形区域代表系统的真实模式空间;图2(c)、(d)闭曲线包围的模型集为k和k+1时刻利用LMS技术确定的基础模型网格;图2(e)、(f)描述了 MEMA算法在k和k+1时刻所利用的动态模型集，由此可知，基础网格M与修正网格C在系统真实模式附近形成了双层覆盖，并且参与状态估计的模型集合更加集中，并接近于系统真实模式.

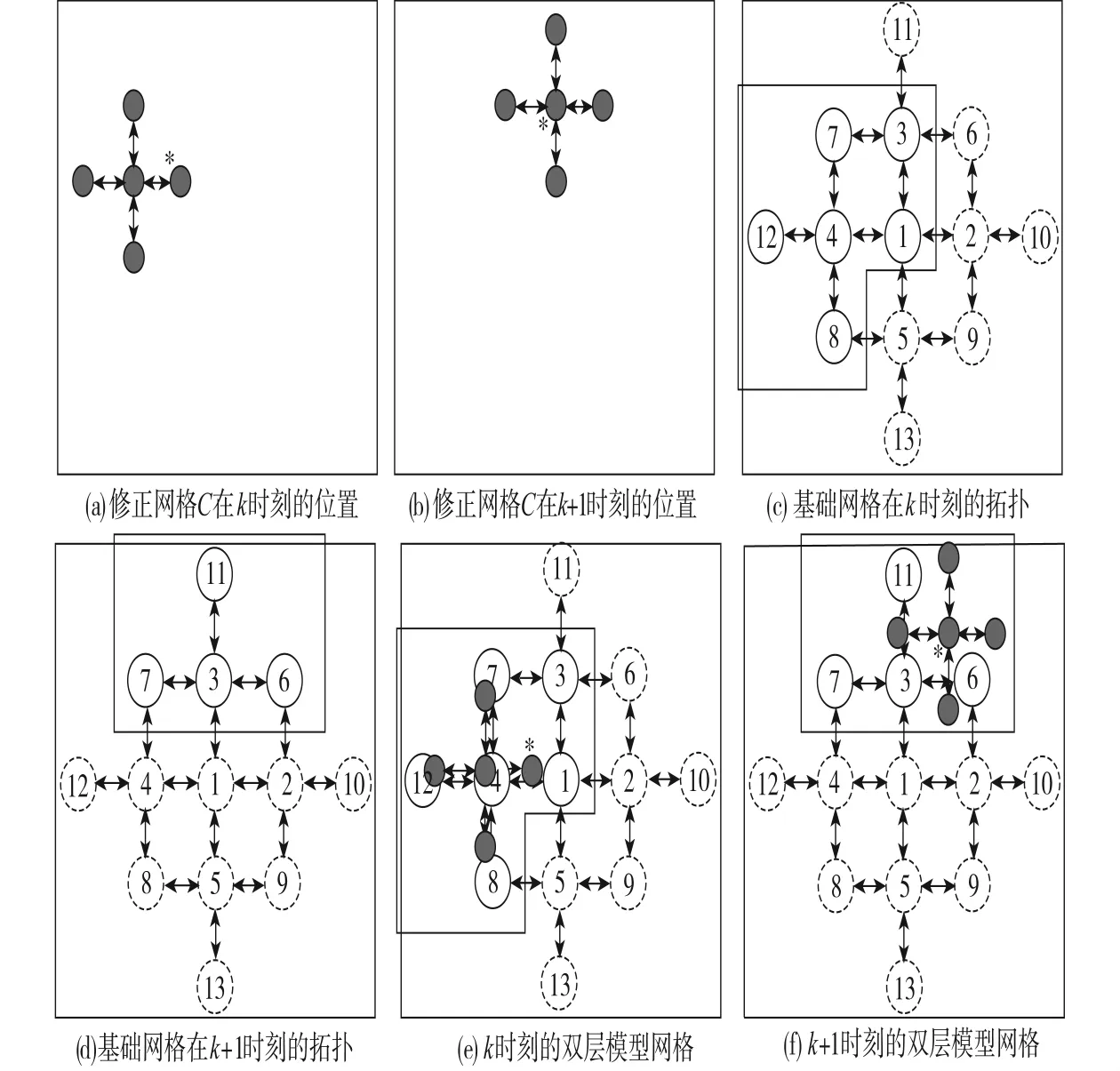
图2 双层网格变结构多模型估计中的模型集拓扑示意Fig.2 The topology of the model set in double layer model grid VSMM

2.3 算法流程

M-EMA算法中系统模式空间Ac定义为［－80，80］.基础网格M模型距离约为40.模型m1～m13的分布见图2(c)～(f)，模型采样时间TM=1 s.修正网格C可能位于系统模式空间中的任何位置，主要依赖于网格C前一时刻的滤波结果，模型最大间距D为待定参数，这里设D=10，模型采样时间TC=0.5 s.模型集C与M之间的转移概率矩阵如图3所示.

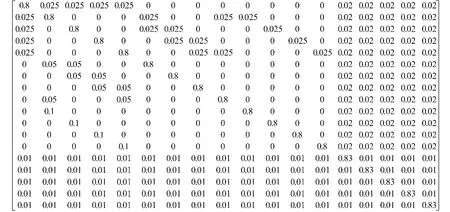
图3 M-EMA中的概率转移矩阵Fig.3 The probability sw itch matrix in M-EMA

M-EMA算法的一个运行周期如图4所示.

1)在时刻 K 基于模型集 Mf=Mk－1－ Ek－1运行VSMM 算法一个递归周期 VSMM［Mf，Mk－1］获得模型的状态估计、估计误差协方差以及模型概率

2)利用AGIMM技术，在一个时间相对细化的尺度上得到对应于时刻K的变结构修正模型网格，作为期望扩张模式集 C=C(Mk－1;M(1)，…，M(q));

3)运行递归 VSMM［Ek，Mk－1］获得状态估计，估计误差协方差以及模型概率

4)将模型集Mf中的模型按照模型的后验概率分为不可能、有效和重要模型，并且令不可能模型的集合为主要模型的集合为

5)如果只有有效模型，则利用最优融合准则，对S1、S3获得的估计结果进行融合，获得基于模型集合Mk=Mf∪Ek的融合结果{，进入下一个递归;

不为空令与主要模型毗邻的模型集合为Ma，则新激活的模型集合Mn=Ma∩Mk运行VSMM［Mn，Mk－1］并将估计结果与 S1、S3 获得的估计结果利用最优融合准则进行估计融合.令Mk=Mf∪C∪Mn，运行VSMM进入下一个循环;

7)如果Muk－1不为空，将其从Mk中删除，进入下一个循环，Mk=(Mf∪C∪Mn)－

3 实验与仿真

3.1 系统模型

目标状态方程和观测方程由式(5)表示:

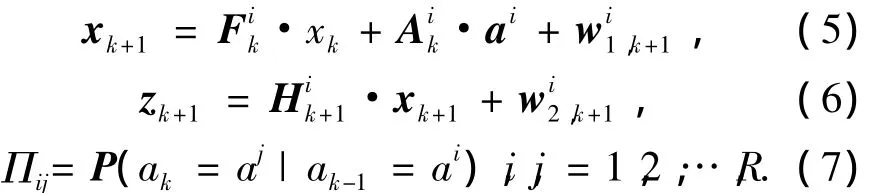
式中:xk和zk分别是状态矢量和观测矢量.ai是加速度矢量.Πij是模型ai到aj的转换概率.

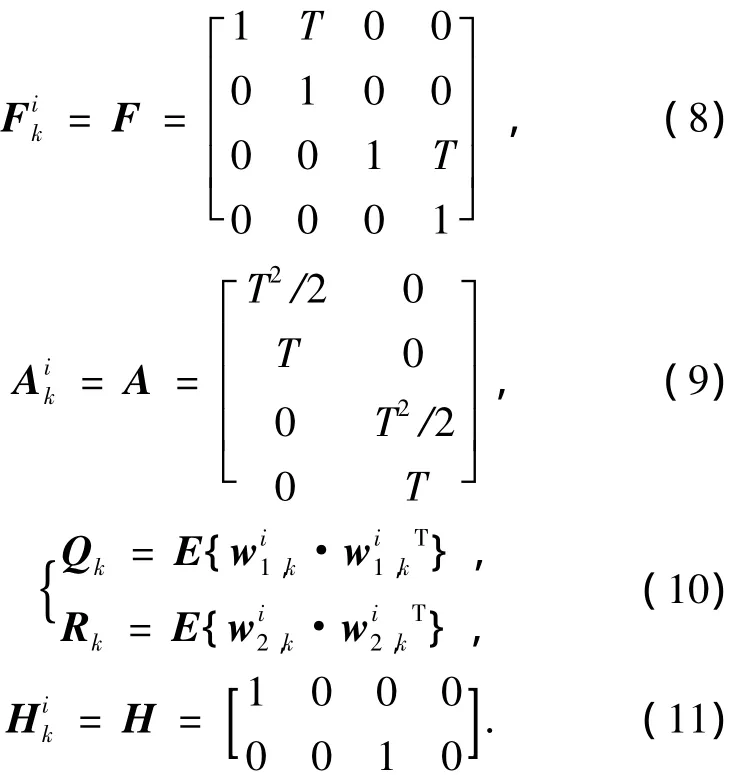
3.2 仿真设计与结果

本文对二维空间上的机动目标跟踪进行仿真.状态矢量由2个坐标上的位置和速度组成，观测矢量由观测到的目标位置组成，加速度矢量由2个坐标上的加速度分量组成，过程噪声和观测噪声协方差分别.

在以下仿真中，位置和距离的单位是m，时间单位是s，速度单位是 m/s，加速度单位是 m/s2.基础网格 M 的初始模型集设为{m1，m2，m3，m4，m5}，各个模型的初始概率为{u1=u2=u3=u4=u5=1/5};修正网格C中Ccen位于模型空间的中心，边缘模型分别位于中心模型的上/下/左/右，且模型间距都为10.各个模型的初始概率同M，初始状态 x0=［0，10，0，10］.噪声方差 Qx=0.2，Qv=0.6，Rx=100.

本文设计了1种不同的强应动运动方式来比较和评价提出的M-EMA算法，对比算法为EMA算法和LMS算法.场景设计如表1所示，仿真时间为100 s，表中序列为目标在X和Y轴上的加速度.仿真场景:假设目标的实际加速度可以在图1(a)中的任意2个节点之间跳变，即目标作强机动.仿真结果如图4、5所示.算法在X、Y轴方向上对位置与速度的估计误差标准差统计结果如表2所示.

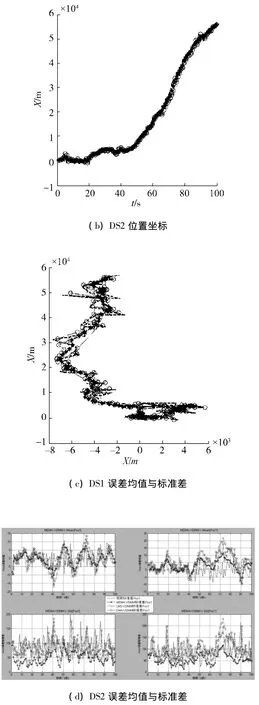
图4 M-EMA算法仿真结果Fig.4 The simulation results of M-EMA

表1 仿真场景设计Table 1 The design of simulation

表2 LMS、EMA、M-EMA算法估计误差标准差比较Table 2 The error std of LMS，EMA and M-EMA

3.3 结果分析

分析仿真结果可知，在仿真场景下，EMA算法和LMS算法会出现严重的偏离，如图4(d)中，X坐标在80 s之后发生严重偏离，Y坐标在60～80 s之间发生严重偏离，而此时的M-EMA算法无论在稳定性还是在精确性上都表现出了明显优势.

4 结论

总结全文可以看出M-EMA算法比较EMA算法和LMS算法具有一定的优势，这种优势是由于M-EMA算法从3个方面突破了EMA算法的局限性:

1)M-EMA算法从模型分布和模型数量上优化了EMA算法中的固定结构模型集;

2)M-EMA算法摆脱了EMA算法中修正模型对固定模型集的依赖，消除了由于固定结构模型集估计的不精确而导致的修正模型的偏差;

3)M-EMA算法利用移动的模型网格取代了EMA算法中单个的修正模型，进一步提高了修正模型集的修正力度.

［1］LI X R，JILKOV Y P.A survey of maneuvering target tracking——part V:multiple-model methods ［J］.IEEE Trans on AES，2005，41(4):1258-1263.

［2］LIX R，ZHANG Y M，ZHIX R.Multiple-model estimation with variable structure——part IV:design and evaluation of model-group switching algorithm［J］.IEEE Trans on Aerospace and Electronic Systems，1999(1):242-254.

［3］LIX R，ZHANG Y M.Multiple-model estimation with variable structure—part V:likely-model set algorithm ［J］.IEEE Trans on AES，2000，36(2):448-466.

［4］LIX R，ZHANG Y M.Multiple-model estimation with variable structure-part VI:expected-mode augmentation ［J］.IEEE Trans on AES，2005，4(3):853-867.

［5］党玲，许江湖.自适应网格交互多模型算法［J］.火力与指挥控制，2004，29(4):51-54.DANG Ling，XU Jianghu.Adaptive grid interacting multiple model algorithm［J］.Fire Control ＆ Command Control，2004，29(4):51-54.

［6］唐婷，何子述.一种改进的自适应网格交互多模型跟踪算法［J］.信号处理，2009，25(5):816-819.TANG Ting，HE Zishu.Amodified adaptive grid interacting multiple model tracking algorithm［J］.Signal Processing，2009，25(5):816-819.

［7］任继山.模型组转换算法在机动目标跟踪中的应用［J］.上海航天，2007，5:54-58.REN Jishan.Application of maneuvering target trackingwith model group switching algorithm［J］.Aerospace Shanghai，2007，5:54-58.

［8］杜在泉，嵇成新，关锦生.一种新的机动目标跟踪中的变结构多模型算法［J］.火力与指挥控制，2010，35(6):144-148.DU Zaiquan，JIChengxin，GUAN Jinsheng.A new variable structure multiple-model algorithm for maneuvering target tracking［J］.Fire Control ＆ Command Control，2010，35(6):144-148.

［9］万永峰，嵇成新，陈阳.跟踪机动目标的一种新的多模型算法［J］.火力与指挥控制，2008，33(4):120-125.WAN Yongfeng，JI Chengxin，CHEN Yang.A new multiple-model algorithm for tracking maneuvering target［J］.Fire Control＆ Command Control，2008，33(4):120-125.

［10］刘士建，郭立，李士民.变结构多模型估计单Kalman滤波跟踪机动目标算法［J］.电路与系统学报，2003，8(5):28-32.LIU Shijian，GUO Li，LIShimin.Variable structure multiple-model and single Kalman filter algorithm for tracking maneuvering target［J］.Journal of Circuits and Systems，2003，8(5):28-32.

［11］伍明，孙继银.一种机器人未知环境下动态目标跟踪交互多模滤波算法［J］.智能系统学报，2010，5(2):127-139.WU Ming，SUN Jiyin.An interacting multiple model filtering algorithm for mobile robots to improve tracking of moving objects in unknow environments［J］.CAAI Transactions on Intelligent Systems，2010，5(2):127-139.