流密码Sosemanuk的区分攻击
李顺波,胡予濮,王艳
(1.西安电子科技大学理学院,陕西西安710071;2.西安电子科技大学计算机网络与信息安全教育部重点实验室,陕西西安710071;3.西安建筑科技大学 理学院,陕西西安710055)
流密码 Sosemanuk[1]是法国电信的 Berbain等人提交的面向软件的快速流密码,经过为期4年的评选,已经成为欧洲eSTREAM计划最终获选的7个流密码算法之一.流密码Sosemanuk是基于流密码SNOW2.0和分组密码SERPENT的加密算法,密钥长度是可变的128bit或256 bit,具有较高的安全性,自今对128 bit密钥还没有比穷举搜索更快的方法,其安全性分析已经成为国内外学者研究的热点.对其现有分析方法有猜测—确定攻击[2-6]和相关攻击[7-8],还未发现有区分攻击的分析结果.
区分攻击是指在统计意义上可以将密钥流与随机序列区分.尽管从攻击结果上看区分攻击是最弱的,但区分攻击也是最灵活的攻击方法,面对区分攻击流密码设计者往往很难做到疏而不漏.许多流密码算法都遭到区分攻击的威胁,如 SNOW[9-11]、Shannon[12]、SN3[13]和 RC4[14]等密码算法.
本文利用区分攻击分析流密码Sosemanuk的安全性,在弱化Serpent1密码特性的前提下,利用线性掩码技术线性逼近FSM和Serpent1;通过建立区分器,需要约2221密钥流比特,就可以把密钥流序列与随机序列相区分,分析结果表明大于2221bit密钥的密码算法是不安全的.
1 区分攻击基本理论
1.1 区分攻击
2002年Coppersmith等提出“区分攻击(distinguishing attack)”[9],通过观察某些输入与输出比特之间的关系来判别这些比特是来自真随机源还是来自密码,将其转化为一个假设检验问题.事实上,它并不是一种攻击形式,而只是判定流密码性质好坏的一个新近提出的严格的安全标准.区分攻击的关键是寻找适当的区分器,更具体地说,区分器是指区分一串密钥流和一串真正随机序列的一种有效算法.区分器是以密钥流的某些弱点为基础的,这些弱点体现出给定的密钥流具有的不随机性,或称为偏差.区分器正是利用这些弱点来设计算法的.
根据Neyman-Pearson引理给出最优检验,所需检测的数据N由统计距离决定,在分布均匀的情况下,N=e-2,其中e为P0和PM1在给定有限集X上的统计距离,即
1.2 线性掩码
掩码技术的基本思想是将输入数据和每一个中间结果都用随机数隐藏起来;通常就是用一串2进制对目标字段进行异或运算屏蔽一些东西.本文采用异或掩码,用“⊕”代替模加和Trans函数运算.

记线性逼近关系Γ·F(x)=Λ·x的偏差为eF,则 εF=|cF(Λ,Γ)/2|.
1.3 Walsh变换和线性逼近
1.3.1 Walsh-Handamard 变换(WHT)
1)设有n维布尔函数f,取n维布尔向量w=(w1,w2,…,wn),令 x·w=x1w1+x2w2+ … +xnwn.定义f的Walsh-Handamard变换F(w)∶
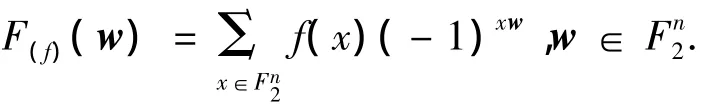

WHT的反变换为
1.3.2 线性逼近
记概率 p(y)=Pr[f(x)=y],则线性逼近Γf(x)=0的相关度为

引理1(最佳逼近定理):
以Pf(x w⊕L)记函数f(x)与仿射函数x w⊕L相等的概率,则有
如果密码函数虽然不是线性的或仿射的,但“很接近”某个线性函数或仿射函数,将对安全性构成致命的威胁.
2 Sosemanuk密码算法
Sosemanuk是Berbain等人设计的基于32 bit字的快速流密码,密钥长度是可变的128 bit或256 bit,初始化向量为 128 bit、384 bit的内部状态.流密码Sosemanuk是基于流密码SNOW2.0和分组密码SERPENT的加密算法,逻辑结构如图1所示,其核心部件由线性移位寄存器(LFSR)、FSM和Serpent1 3部分组成.
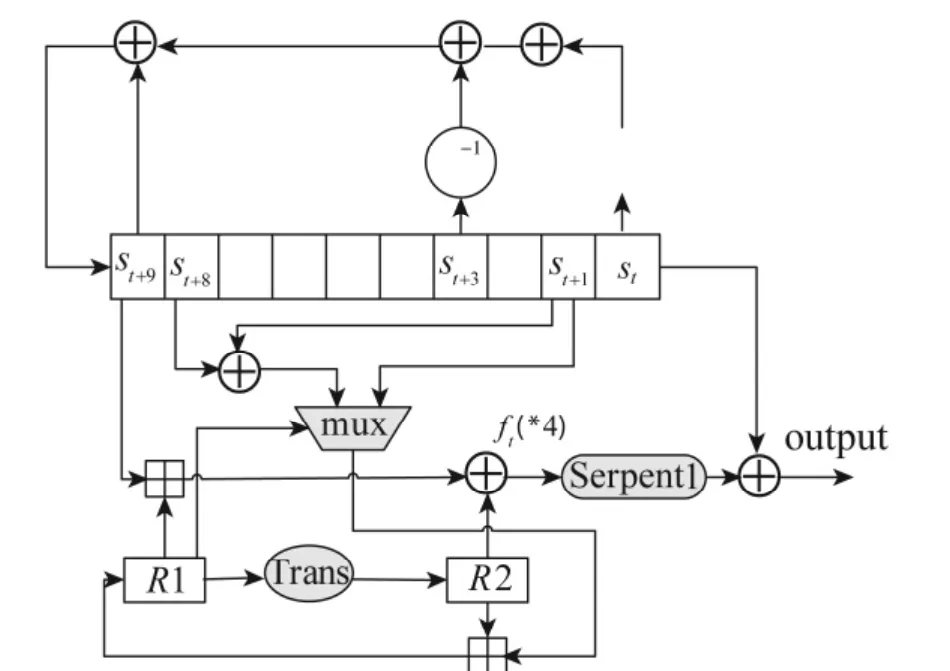
图1 Sosemanuk的逻辑结构Fig.1 The structure of Sosemanuk
2.1 线性移位寄存器
Sosemanuk的LFSR是定义在有限域GF(232),包含10个32 bit的寄存器 si,1≤i≤10.线性递归序列:

对应的特征多项式为
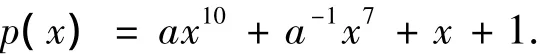
其中,a是定义在 GF(28)上多项式 P(x)的根,P(x)=x4+b23x3+b245x2+b48x+b239.b 是二元多项式 Q(x)的根,Q(x)=x8+x7+x5+x3+1.
2.2 有限状态机(FSM)
记FSM在时刻t的状态为(R1t,R2t),则状态反馈为

其中:为模232加,⊕为按比特异或;lsb(x)为x的最低位比特.

即:
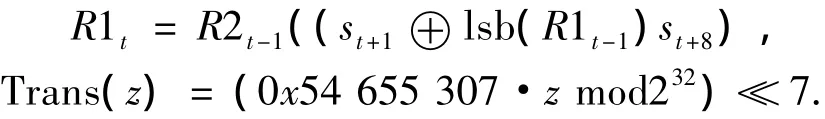
2.3 Serpent1
Serpent[15]是由 Anderson 等设计的 AES 的候选密码算法,32轮SPN结构,其分组大小是128位,8个不同的 S-盒{S0,S1,…,S7}.Serpent1 是一轮的Serpent,没有密钥加法和线性变换;其S-盒为S2={8,6,7,9,3,12,10,15,13,1,14,0,11,5,2}.4 个32 bit字输入,4个32 bit字输出.密钥流生成算法为
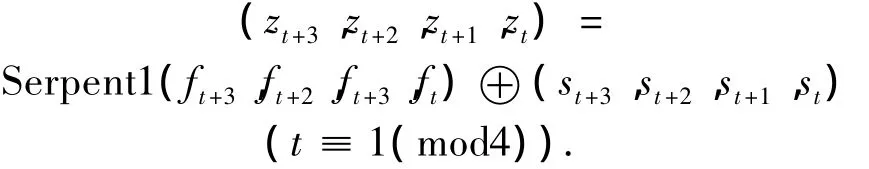
3 区分攻击Sosemanuk
本节讨论利用文献[7]线性掩码技术区分攻击Sosemanuk.首先分别给出了FSM和Serpent1的线性逼近,然后构建区分器,利用计算机模拟获得线性逼近的偏差;最后获得区分需要的密钥流比特.
3.1 线性逼近FSM
令 at=lsb(R1t),ai∈{0,1},若存在 32 bit的线性掩码,用比特异或‘⊕’代替所有的运算(模加和Trans函数运算),则FSM状态转移函数变为
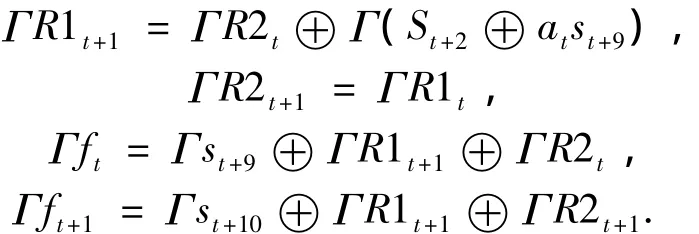
以上4式相加则有
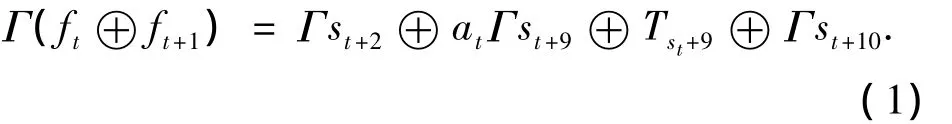
为了提高上式线性逼近偏差的精度,采用不同的线性掩码Φ,如图2所示;其线性掩码对模加和Trans函数的相关度分别为

则线性逼近式(1)的相关度为
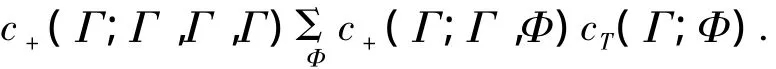

图2 Sosemanuk的线性掩码Fig.2 The linear masking of Sosemanuk
3.2 线性逼近Serpent1
Serpent1是取自分组密码Serpent的第3个S-盒,S2={8,6,7,9,3,12,10,15,13,1,14,4,0,11,5,2},S2有最大的线性相关度1/2,则由图2(b)得到的线性逼近关系式:

成立的相关度为(1/2)wt(Γ),其中w(t)为汉明重量,即1的个数.
由式(1)、(2)可得到下列线性逼近:

成立的相关度为


实验结果表明,当T取重量为4的{25,24,14,0}时,相关度为 cΓ=2-21,41.
所以,相应地线性逼近式(4)的偏差为eΓ=2-22,41.
因为 at∈{0,1},则 at=0 的概率为 1/2,即atΓst+9⊕Γst+9=0成立的概率为 1/2,因此,由式(3)线性逼近:

成立的相关度为
3.3 建立区分器
结合Sosemanuk的线性递归序列和式(4)的线性关系,消去中间状态,得到仅关于输出密钥流z的方程.建立如下区分器:
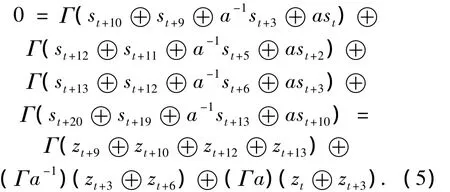
利用有限域理论,实验仿真结果如表1所示.

表1 线性掩码对应的偏差Table 1 The bais to some linear masking
依据堆积引理,区分器式(5)成立的概率为
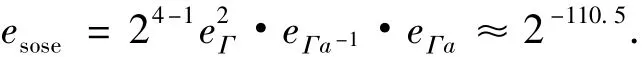

表2 比较Sosemanuk的各种攻击结果Table 2 Comparison of the attack results on Sosemanuk
4 结束语
流密码Sosemanuk是最终获选eSTREAM计划的7个密码算法之一,它软硬件实现简单并有较高的安全性,因此极有可能成为下一代通信加密算法.通过弱化Serpent1的密码特性,利用线性掩码技术线性逼近FSM和Serpent1,建立区分器,需要约2221密钥流比特就可以区分密钥流序列.虽然区分攻击结果不及文献[5]中猜测—确定攻击的时间复杂度;但该文首次利用区分攻击对流密码Sosemanuk的安全性进行了有益的尝试.同时,区分攻击不必借助于线性序列源,对基于非线性序列源的流密码算法具有潜在的威胁,将是未来流密码分析的重要方向之一.
[1]BERBAIN C,BILLET O,CANTEAUT A,et al.Sosemanuk,a fast software-oriented stream cipher[EB/OL].[2005-05-26].Cryptology ePrint Archiive,http://www.ecrypt.eu.org/2005/027.pdf.
[2]AHMADIH,EGHLIDOST,KHAZAEIS.Improved guess and determine attack on Sosemanuk[EB/OL][2005-12-25].http://www.ecrypt.eu.org/stream/sosemanukp3.html.
[3]TSUNOO Y,SAITO T,SHIGERIM.Evaluation of Sosemanuk with regard to guess-and-determine attacks[EB/OL].[2006-01-02].http://www.ecrypt.eu.org/stream/sosemanukp3.htm l.
[4]DING Lin,GUAN Jie.Guess and determine attack on Sosemanuk[C]//Fifth International Conference on Information Assurance and Security-CIAS2009.Xi'an,China,2009:658-661.
[5]FENG Xiutao,LIU Jun,ZHOU Zhaocun,et al.A bytebased guess and determine attack on Sosemanuk[C]//Advances in Cryptology-Asiacrypt 2010.LNCS 6477.Berlin:Springer-Verlag,2010:146-157.
[6]张海霞,胡予濮,柴进.针对Sosemanuk的猜测-确定攻击[J].计算机工程,2011,37(4):170-171.ZHANG Haixia,HU Yupu,CHAI Jin.Guess and determine attack on Sosemanuk[J].Computer Engineering,2011,37(4):170-171.
[7]LEE JK,LEE D H,PARK S.Cryptanalysis of sosemanuk and SNOW 2.0 using linear masks[C]//Advances in Cryptology-Asiacrypt 2008.LNCS 5350.Berlin:Springer-Verlag,2008:524-538.
[8]CHO JY,HERMELINM.Improved linear cryptanalysis of Sosemanuk[C]//Information,Security and Cryptology-ICISC 2009.LNCS 5984.Berlin:Springer-Verlag,2010:101-117.
[9]COPPERSMITH D,HALEVIS,JUTLA C.Cryptanalysis of stream ciphers with linear masking[C]//Advances in Cryptology-Crypto 2002.LNCS 2442. Berlin:Springer-Verlag,2002:515-532.
[10]WATANABED,BIRYUKOV A,CANNIERECD.A distinguishing attack of SNOW 2.0 with linearmasking method[C]//Selected Areas in Cryptography-SAC 2003,LNCS 3006.Berlin:Springer-Verlag,2004:222-233.
[11]NYBERG K,WALLEN J.Improving linear distinguishers for SNOW 2.0[C]//Fast Software Encryption-FSE 2006,LNCS 4047.Berlin:Springer-Verlag,2006:114-162.
[12]AHMADIAN Z,MOHAJERI J,SALMASIZADEH M,et al.A practical distinguisher for the Shannon cipher[J].The Journal of Systems and Software,2010(83):543-547.
[13]KELLER N,MILLER SD.Distinguishing attack on stream ciphers based on arrays of pseudo-random words[J].Information Processing Letters,2010,110:129-132.
[14]SEPEHRDAD P,VAUDENAY S,VUAGNOUX M.Statistical attack on RC4 distinguishing WPA[C]//Advances in Cryptology-Eurocrypt 2011, LNCS 6632. Berlin:Springer-Verlag,2011:343-363.
[15]ANDERSON R,BIHAM E,KNUDSEN L R.Serpent:A proposal for the advanced encryption standard[EB/OL].[1998-08-21].http://www.cl.cam.ac.uk/rja14/serpent.htm l.

