车辆自适应巡航控制算法的设计与仿真＊

黄 珍 吴浩然 库 峰 徐小强

（武汉理工大学自动化学院 武汉 430033）

0 引 言

车辆自适应巡航控制系统（adaptive cruise control，ACC）是智能交通系统（ITS）领域中先进车辆控制及安全系统（AVCSS）开发的一个重要方面.ACC是在传统巡航控制技术基础上发展起来的，因此既具有传统巡航控制的定速巡航能力，同时可通过雷达等车载传感器采集信息，自动调整车辆行驶速度，保持本车与前行车辆的安全间距，从而降低驾驶员操作量、减轻驾驶疲劳，提高车辆的主动安全性及驾驶舒适性.

国内外对ACC 系统的研究主要集中在车载传感器技术、信息融合技术以及控制策略选取等软硬件技术上.其中如何选取控制策略是实现ACC 系统功能的关键技术.目前，国内外车辆ACC的典型控制算法主要有分工况控制和分层控制两种.分工况控制算法将控制工况分为驱动控制与制动控制［1］、速度控制与距离控制［2］，或分为定速与跟车［3］等多种工况分别进行控制.分层控制，即上层控制器依据传感器采集到的车距和相对速度，以及驾驶员设定的车辆时距和巡航速度来决定车辆的纵向加速度.下层控制器依据上层控制器计算出的车辆期望加速度对刹车和油门进行控制，从而使车辆保持设定车速或车距.

其中，分工况控制一般针对不同的控制工况采用特定的控制模型，当多个工况间相互切换时，控制状态变量存在间断不连续等问题，影响了控制效果.分层控制不存在工况间的切换，避免了这个问题.但是，分层控制算法在实际运用上也存在困难.首先，现有的大部分传感器（如激光雷达、微波雷达、毫米波雷达等）只能测量相对距离和前、自车速度，而无法直接测得加速度.因此，前、自车加速度只能通过间接方法（如速度值对时间求微分）求得，这样不仅引入了额外的计算误差，某些情况下（如速度曲线在某一点不可微）系统甚至会出现不可预知的错误.其次，现有的上层控制器所采用的算法如线性最优控制［4］、线性二次型最优控制（LQ）、时间能量最小最优控制（TEM）以及LQ 和TEM 的混合算法［5］等，这些算法普遍较复杂，系统运算量较大，对系统运算能力需求较高，因此增加了技术难度和成本.

针对上述问题，笔者在分层控制的基础上，提出了一种根据当前车距以及前、自车车速，基于安全、舒适因素综合因素决策车辆期望速度，从而控制车辆的车距和车速的ACC 控制算法.该算法将传统ACC控制系统中求取期望加速度改为决策期望车速，有效减少了系统运算量，提高了系统响应速度.

1 系统方案设计

作者构建的ACC 控制系统以车辆直线行驶为主，考虑到尊重驾驶员的驾驶习惯以及安全因素，系统将不控制车辆主动变换行驶车道.

将车辆运行状态分为2种工作模式：

1）定速巡航模式 当前方无车或车距大于设定值时，系统工作在该模式，系统根据用户设定的目标车速定速行驶.

2）安全跟车模式 当与前方车辆的车距小于等于设定值时，系统进入跟车模式.车辆首先调整车速使车距达到设定值.若前车车速大于用户设定的巡航车速，则进入定速巡航模式；若前车车速小于等于用户设定的巡航车速，则车辆保持与前车相同的车速行驶，使车距稳定在设定值.

车速控制器共有5个输入参量，包括3个传感器采集量（前／自车车速、当前车距）和两个用户设定值（目标巡航车速、目标车距）.控制器的输出为节气门开度和刹车力矩.

按照分层控制的思想，将控制器分解为2层.（1）上层控制器输入量为：前车车速、当前车距、目标巡航车速、目标车距，输出为自车期望车速.（2）下层控制器根据上层算法提供的期望车速和当前的自车车速，输出节气门开度和刹车力矩值，从而控制车速.控制器结构见图1.

图1 车速自适应控制器结构示意图

2 控制器细化设计

2.1 上层控制器设计

上层控制器首先根据传感器采集信息和用户设定值判断当前工作模式，输出为车辆当前的期望车速.若为定速巡航模式，则直接输出用户设定巡航车速作为当前期望车速；若为跟车模式，则需通过车距控制算法计算出当前期望车速.

目前国内外的车距控制算法有线性最优控制、LQ＆TEM、神经网络控制［6］以及滑模控制［7］等，这些算法结构较复杂，计算量大，具体实现难度较大.因此，这里探寻出一种更为简单的车距控制算法.

因为要保持车距不变，所以在车距稳定时，自车与前车车速必然相等.因此，可以前车车速为依据，使自车车速以某种规律趋近于前车车速.综合考虑安全、驾驶舒适性等因素，建立理想车速规律表.

设当前实际车距为d，目标车距为ddes，前车车速为vq，设定巡航车速为vs，自车车速为v，当前期望车速为vdes，车距模块输出期望车速为vcj.

计算车距误差Δd，即

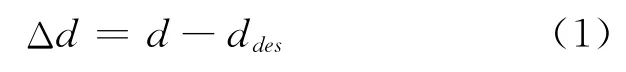
将Δd 的取值范围分成n 个区间（L1，L2，L3，…，Ln），每个区间对应一个系数k值，当前时刻的期望车速.即

系数k＝（k1，k2，k3，…，kn）的取值规律是随着Δd 的由负到正k 先由一个0到1之间的值逐渐增大到1，再逐渐增大.取值举例见表1.

表1 系数k、区间L、Δd与vcj的关系表

而上层控制器的输出vdes则由vcj与vs比较后的较小值决定，即

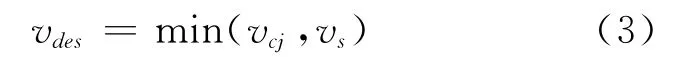
2.2 下层控制器设计

下层控制器相当于一个定速巡航控制器，即控制器与被控车辆形成闭环，使车辆按照期望车速行驶.

下层控制器根据加速和减速两种情况，将节气门控制和刹车控制独立设计，通过切换逻辑使它们分别作用于车辆.

2.2.1 节气门控制

节气门控制采用PID 算法，考虑到不同期望车速之间的平稳切换，可采用增量式PID 控制，如式（4）和（5）所示.

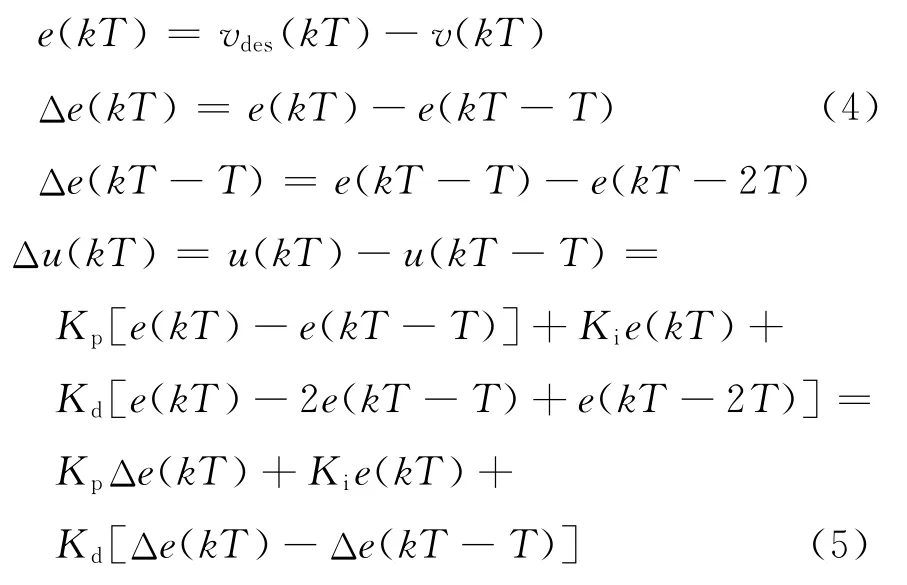
式中：Δu（kT）为第k次采样时刻控制器输出值的增量；Kp为比例系数；Ki为积分系数；Kd为微分系数；vdes（kT）为当前期望车速；v（kT）为自车第k次采样时刻的实际车速；T 为采样周期.

2.2.2 刹车控制

根据ACC控制原理，ACC 控制器在刹车方面主要有以下2个特点：（1）为了保证乘坐的舒适性，并且系统不会产生让驾驶员感到惊奇的行为，汽车的刹车减速度应小于2.5 m／s2；（2）要求刹车控制算法简单、精度高，且响应迅速.

基于以上特点，本系统将制动力矩作为刹车控制的输出值，在已知实际车辆每个车轮制动压力和制动力矩转换系数的前提下，可以方便地将系统的输出值转换为制动力，由车辆的ABS 和EBD 系统分配给每个车轮.

根据刹车前实际车速与期望车速的差值Δv，系统将制动力矩分档输出，刹车力矩的每一档对应Δv的一段取值区间，Δv 越大，对应的制动力矩越大.同时，保证最大制动力矩对应的刹车减速度应小于2.5m／s2.如遇到紧急情况需要更大制动力矩时，系统发出警报提醒驾驶员介入刹车.分档刹车效果如图2所示.

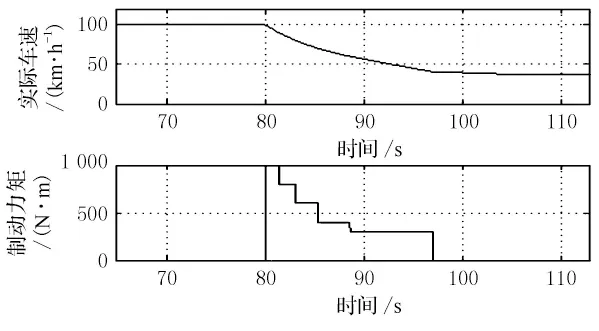
图2 分档刹车效果图

2.2.3 节气门、刹车控制的切换

在实际车辆控制中，油门和刹车是分时作用的，当节气门开度非最小值时制动力矩应为0，而当制动力矩不为0时，节气门开度应为最小值.因此，控制好它们之间的切换尤为重要.

本系统将当前期望车速vdes乘以一个大于1的系数p，再与自车车速v求差值，以此作为节气门、刹车控制的切换规则，如表2.

表2 节气门、刹车控制的切换规则

3 仿真实验及结果分析

本算法在MATLAB－R2009a环境下建立了仿真模型，整个系统通过Matlab／Simulink实现，包括四速自动档车辆纵向动力学模型、控制器模型和传感器信号模型等.车辆纵向动力学模型根据文献［8］提供的方法，以一款1.5L，72kW 自动档轿车为蓝本构建，其中发动机模型、液力耦合器模型及车辆驱动系模型利用Matlab／Simulink框图实现，自动变速器模型利用Matlab／Stateflow 实现.仿真系统结构见图3.

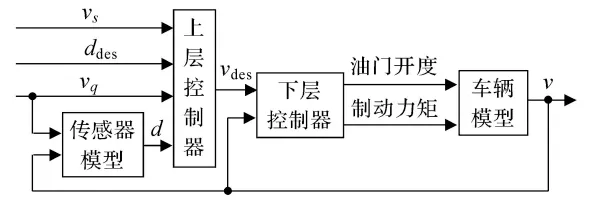
图3 仿真系统结构图

为了验证控制器的控制效果，设置了三种前、自车行驶情景进行模拟仿真.

用户设定值：所有情景中，自车定速巡航速度始终设定为120km／h，目标车距始终设定为80m.

仿真情景1 前车匀速.

在0～40s时前方无车，本车行驶在定速巡航模式，巡航车速为120km／h.在40s时，前方60m 处发现速度为100km／h的前车，本车进入跟车模式.仿真结果见图4、图5.

仿真情景2 前车变速（不大于巡航目标车速）.

在0～40s时前方无车，本车行驶在定速巡航模式，巡航车速为120km／h.在40s时，前方60m 处发现速度为100km／h的前车，本车进入跟车模式.在80s时，前车加速到110km／h，在180s时，前车减速到90km／h.仿真结果见图6、图7.

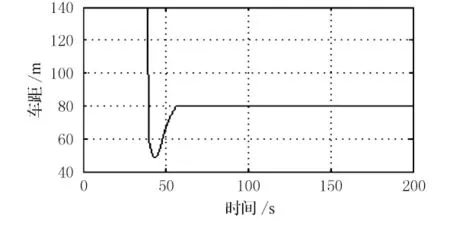
图4 情景1时车距变化曲线

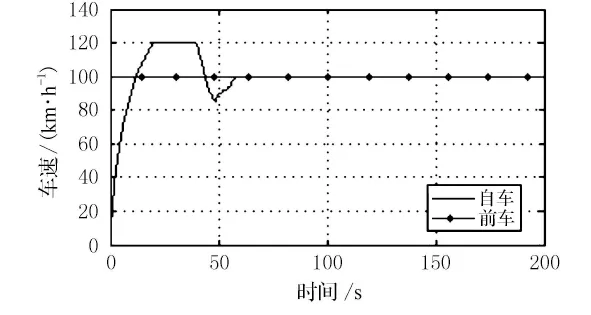
图5 情景1时前方车辆与本车速度变化曲线

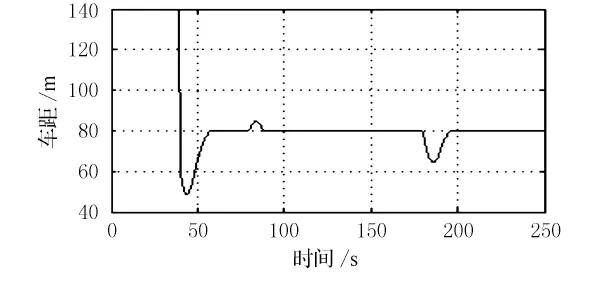
图6 情景2时车距变化曲线

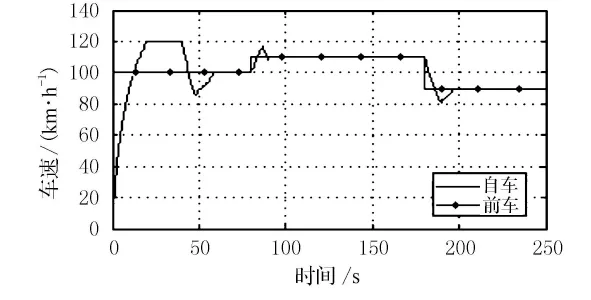
图7 情景2时前方车辆与本车速度变化曲线

仿真情景3：前车变速（有时高于巡航目标车速）

在0～40s时前方无车，本车行驶在定速巡航模式，巡航车速为120km／h.在40s时，前方60m 处发现速度为100km／h的前车，本车进入跟车模式.在80s时，前车加速到130km／h，此时前车车速大于设定的巡航速度且车距不小于设定车距，本车进入定速巡航模式.在120s时，前车减速到90km／h，此时车距大于设定值，本车仍然定速巡航，当车距缩小到设定值附近时，本车进入跟车模式.仿真结果见图8、图9.

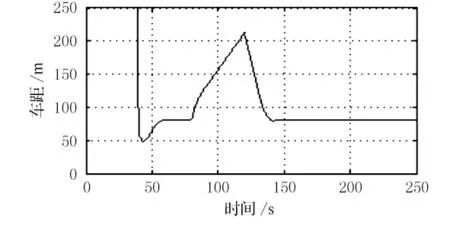
图8 情景3时车距变化曲线

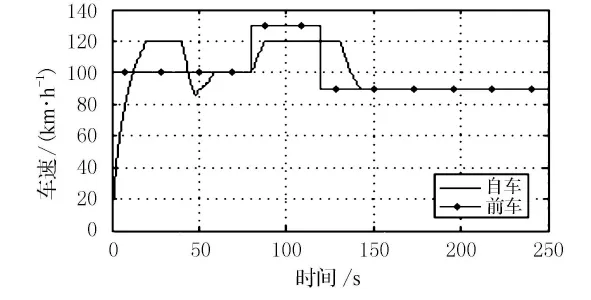
图9 情景3时前方车辆与本车速度变化曲线

从以上仿真结果可以看出，本车能较快跟随前车，车距控制效果稳定，调整时间短，速度响应曲线能很好地满足控制的需要.

三种情景下，定速模式车速控制稳态误差在0.02km／h以内，超调量小于0.6%；跟车模式车距稳态误差在0.15 m 以内，超调量小于1.8%.自动刹车的最大减速度控制在2.5m／s2以内，根据研究，该减速度能很好地保证乘坐的舒适性.

4 结 论

在车速跟踪及PID 控制的基础上建立了车辆ACC分层控制算法.多种工况的仿真结果表明，该算法以较小的数据量和计算量获得了较好的响应速度和控制精度，有效地实现了车辆ACC系统的控制目标.本系统在加、减速度上还综合考虑了乘客的舒适度.

下一步研究工作中，将从人性化决策以及节能的角度进一步优化算法，建立功能更加全面的智能车辆自适应巡航控制系统.

［1］IOANNOU P，XU Z.Throttle and brake control systems for automatic vehicle following［R］.California PATH Research Paper，UCB－ITS－PRR－94－10，1994.

［2］YI Kyongsu，HONG Jinho，YOUNG Dokwon.A vehicle control algorithm for stop－and－go cruise control［J］.Proceedings of the Institution of Mechanical Engineers，2001，215：122－128.

［3］ WALTER J.Adaptive cruise control for coaches［C］／／AVEC′96International Symposium on Advanced Vehicle Control at the Aachen University of Technology，1996.

［4］YI Kyongsu，YOUNG Dokwon.Vehicle－to－vehicle distance and speed control using an electronic－vacuum booster［J］.JSAE Review，2001，22：403－412.

［5］LI Keqiang，GAO Feng，ZHENG Sifa，et al.A longitudinal control algorithm of upper layer controller design for automotive vehicles［C］／／6th Int′l Symposium on Advanced Vehicle Control，2002：168－176.

［6］张浩然，王 炜，任 刚.基于相关分析的跟驰模型及其稳定性［J］.武汉理工大学学报：交通科学与工程版，2008，32（4）：581－584.

［7］李以农，冀 杰，郑 玲，等.智能车辆自适应巡航控制系统建模与仿真［J］.中国机械工程，2010，21（11）：1374－1381.

［8］侯德藻，高 锋，李克强，等.应用于汽车主动避撞系统的车辆纵向动力学模型［J］.清华大学学报：自然科学版，2004，44（2）：258－261.