北斗一代用户机定位精度分析

张德欣，于 鹏，李 鹏，魏 勋，周含冰

(中国人民解放军63880部队，河南洛阳471003)

0 引言

北斗一代卫星导航定位系统的建立摆脱了在卫星导航定位领域受制于人的局面，研究北斗一代独特的“双星定位”精度特性至关重要。北斗用户机实际使用和测试过程中，用户更加关心的是在不同情况下东北天坐标系下eon平面的定位误差，而国内现有文献只是定性地在空间直角坐标系下进行了北斗系统的定位精度分析，不满足北斗用户实际使用需求。

通过建立北斗一代用户机东北天坐标系下的定位精度分析模型，重点对无标校平坦地区、无标校起伏地区、有标校平坦地区和有标校起伏地区4种情况下eon平面的定位精度进行了仿真分析。

1 北斗一代系统组成和工作原理

1.1 系统组成

北斗一代导航定位系统由2颗地球同步卫星、1颗在轨备份卫星、中心控制系统、标校系统和各类用户机构成，各部分通过出站链路(即中心控制系统→卫星→用户)和入站链路(即用户→卫星→中心控制系统)相连接。地球同步卫星又称为空间段，其余部分即为地面应用系统。

地球同步卫星:完成中心控制系统和用户机装备之间的双向无线电信号转发。

中心控制系统:完成全系统信息的产生、收集、处理与工况监控。

标校系统:为卫星轨道确定、电离层校正和气压测高校正提供距离观察量和校正参数。

用户机设备:实现定位、导航、通信和定时功能。

1.2 工作原理

北斗一代系统采用3球交会的测量原理进行定位，即已知的2颗同步卫星为2个球心，以2球心至用户的距离为半径可做2个球面;第3个球面是以地心为球心，以地球半径加上用户所在位置高程为半径的球面，3个球面的交会点排除镜像点即为用户的位置。定位原理示意图参阅相应文献[1]。

系统的工作过程是:首先由中心控制系统经2颗卫星转发器同时向服务区内的用户广播询问信号，用户响应其中1颗卫星的询问信号后发送响应信号，经2颗卫星转发回中心控制系统进行接收解调。对定位申请，中心控制系统测出2个时间延迟后算出用户到2个卫星的距离，同时从存储在计算机内的数字化地形图查寻到用户高程值，从而最终计算出用户所在点的三维坐标，经加密后发送给用户。

2 定位精度分析

2.1 误差来源

与GPS定位原理不同，北斗一代系统“双星”定位系统的定位误差主要由测量误差、大地高程误差以及用户机与卫星的几何分布关系共同决定。其中用户机与卫星的几何分布关系主要表现为用户机所处地理位置对定位精度的影响，而测量误差[1，2]主要包括4个方面:①与卫星有关的误差。这部分误差主要包括卫星星历误差和卫星设备延迟，是由于地面监控部分不能对卫星的运行轨道和卫星设备延迟做出绝对准确的测量、预测而引起的。②与信号传播有关的误差。北斗一代定位信号的传播需要穿越大气层，而大气层对信号传播的影响表现为大气延时。大气延时误差通常被分成电离层延时和对流层延时2部分。不同于GPS，多路径效应基本不影响定位精度。③与接收机有关的误差，主要指接收机的设备延迟。④与中心控制系统的误差。中心控制系统较好测距码分辨率和测量噪声对定位精度影响较小，而由中心控制系统查询数字化地图得到的大地高程误差在平坦地区为几米到十几米，在地形起伏大的不规则地区高程误差迅速增大到几十米。

因此，高程误差是限制北斗一代系统定位精度的主要因素之一。

2.2 精度分析

根据文献[3]可知，在距离测量值与高程测量值分别独立且满足高斯分布的条件下，在空间直角坐标下由测量误差和几何分布共同决定的北斗一代系统定位误差可以表示为:

不同于GPS定位精度误差分析方程的是，式(1)中测量误差矩阵B由2部分组成，=分别为接收机与卫星Ⅰ与卫星Ⅱ之间伪距测量误差的方差，由卫星、信号传播、接收机和中心控制系统4个方面共同决定;σ2h为用户高程测量误差的方差，由数字化地形图决定。因此北斗一代系统定位精度误差分析方程无法表达为几何精度因子与误差矩阵的乘积，这里将N命名为几何分布矩阵。

由于使用需要，北斗一代用户机需要考核的指标通常为东北天坐标系下eon平面的定位精度，而式(1)是空间直角坐标系下的定位精度误差分析方程。因此，以站心坐标系中用户机位移量作为定位方程组中的状态变量，通过坐标转换[4]得到站心坐标系下的定位精度误差分析方程如下:

式中，σH为水平定位误差标准差;G为东北天坐标系下的几何分布矩阵;θ、α分别表示用户机与卫星的仰角和方位角，可根据式(6)和式(7)计算得到，Δu、Δe、Δn分别为用户机与卫星距离在东北天坐标系下的投影。

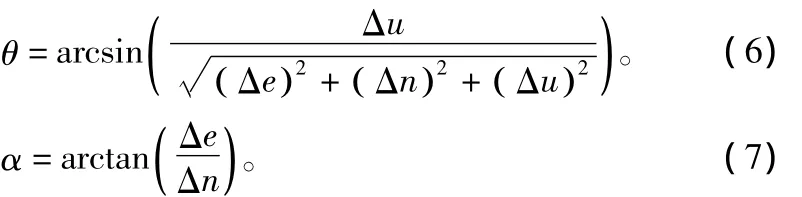
更加关心的是如何利用式(3)分析用户机在大地坐标发生变化时对定位精度的影响，而大地坐标与东北天坐标的转换关系[4]见式(8)～式(12)。其中，Δx、Δy、Δz分别为地心直角坐标系下，用户机与卫星、地心之间的坐标差;N为基准椭球卯酉圆曲率半径;e=0.081 8为地球基准椭球体的偏心率;a=6 378 137 m为地球基准椭球体的长半径;λ、φ、h为用户机的大地坐标。

2.3 仿真计算

已知北斗一代2颗地球同步卫星的大地坐标分别为:(80°E，0°，36 000 km )、(140°E，0°，36 000 km )，设定用户机大地高程为0 m。忽略用户机位置变化对大气时延的影响，分别对以下4种情况下eon平面的定位精度进行仿真计算，有效区域设定为(85°E～135°E，5°N～55°N)。

2.3.1 无标校站平坦地区

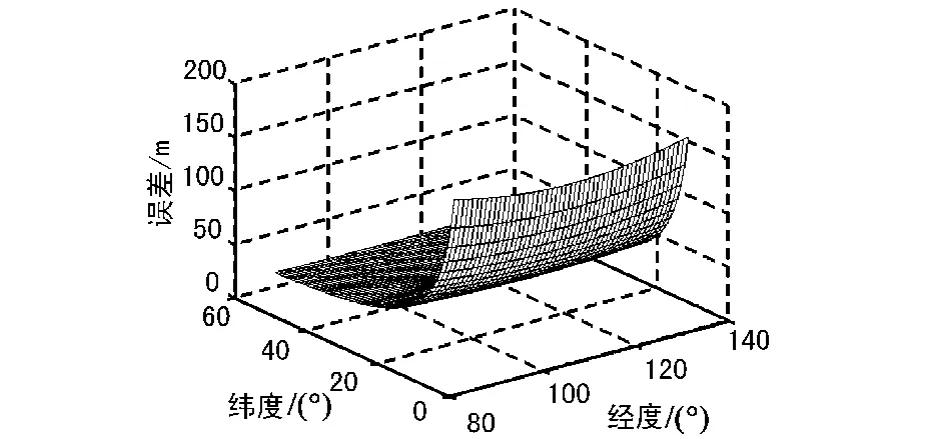
图1 无标校平坦地区定位精度误差分布

2.3.2 无标校站起伏地区

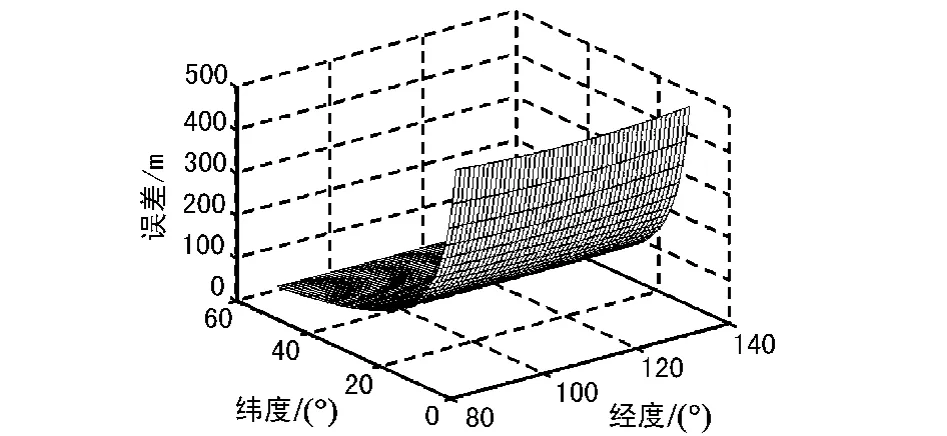
图2 无标校起伏地区定位精度误差分布

2.3.3 有标校站平坦地区

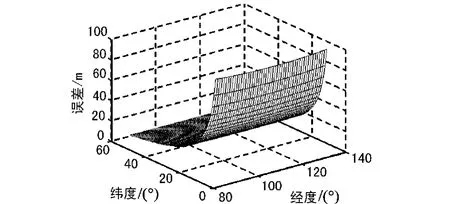
图3 有标校平坦地区定位精度误差分布

2.3.4 有标校站起伏地区

σ2ρ1= σ2ρ2=3 m，σ2h=50 m，仿真结果如图 4所示。

图4 有标校起伏地区定位精度误差分布

3 仿真结果分析

从仿真结果图1～图4分析可以得到以下结论:①用户机位置经度变化对定位误差影响较小;②用户机定位误差随纬度的升高而变小，总体上呈现南高北低的特点;③用户机位于起伏地区相对平坦地区误差较大;④用户机位于平坦地区时无标校相对于有标校时定位误差较大，而位于起伏地区时由于高程误差成为主要制约因素二者误差基本相当;⑤主要范围内无标校平坦地区定位误差在100 m以内，有标校平坦地区定位误差在20 m以内。

由于仿真结果忽略了用户机位置对大气时延的影响，而实际上高纬度地区大气时延误差较大，导致无标校地区定位误差随纬度升高而降低的趋势变小，有标校地区在广域差分原理下大气时延基本不受影响。

4 结束语

根据仿真结果分析，在主要范围内普遍设有标校站的现状下，用户在地势起伏较大的地域可以通过测高方式提高定位精度，需要利用伪卫星技术[1，5，6]对“双星定位”系统进行改进。

[1]隋 艺.北斗卫星和伪卫星组合定位系统研究[D].西安:西北工业大学，2004:42－56.

[2]孙国良，丁子明.双星系统工作方式改进的讨论[J].电子学报，2001，29(9):1 218 －1 220.

[3]戴邵武，马长里，廖 剑.“北斗一代”导航定位系统分析与研究[J].计算机与数字工程，2010，38(3):57 －59.

[4]谢 钢.GPS原理与接收机设计[M].北京:电子工业出版社，2011.

[5]王 玮，刘宗玉，谢荣荣.伪卫星辅助的北斗定位系统的GDOP 研究[J].空间科学学报，2005，25(1):57 －62.

[6]马卫华，袁建平.“北斗”系统低纬度区域定位精度增强方案探讨运筹学[J].全球定位系统，2005(3):46－50.