带通采样时钟沿抖动对解调性能的影响分析
张建志,张丽娜
(1.空军驻石家庄地区军事代表室,河北石家庄050081;2.中国电子科技集团公司第五十四研究所,河北石家庄050081)
0 引言
数字化中频接收机就是将接收到的射频信号下变频到可以处理的中频后,在此中频的基础上进行数字化,再用现代信号处理技术来实现信号的解调、提取和处理。理论上,根据奈奎斯特定理和香农定理,可以用2倍以上信号带宽的采样速率对中频带通信号实现无失真的采样,带通采样的应用可以简化中频复杂度,提高后续数字处理的灵活性,减少对关键器件的要求,同时大大节省运算量。中频带通采样技术已被广泛应用于现代军用或商用无线通信领域。
1 基本原理
采样时钟抖动是时钟源的固有性质,它与输入的信号无关,采样时钟抖动在采样上的表现是使采样位置发生偏离。
采样时钟抖动的影响与采样信号的频率有关系,相同时钟抖动的情况下,信号的频率越高,对时钟抖动的敏感度越大。在中频系统中,信号的频率都很高,带通采样时钟的抖动会对系统的解调性能产生影响,因为采样时钟的抖动是随机的,存在不确定性,所以后端载波恢复对时钟抖动引起的相位偏差不起作用。因此,中频采样时钟抖动问题是数字化中频中带通采样技术的关键问题,下面重点针对中频采样时钟的抖动性问题进行研究。
2 时钟沿抖动对信噪比影响
对于MPSK调制信号,设基带发送的理想信号表示为:
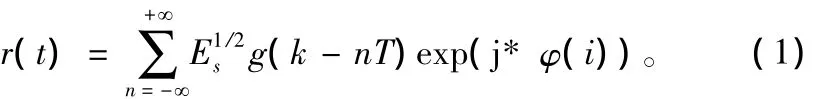
式中,Es为码元能量;T为码元周期;φ(i)为第i个码元的调制相位。
理想中频信号表示为:

下变频后的理想信号表示为:

式中,ω0为载波频率;g(t)为基带滤波器,
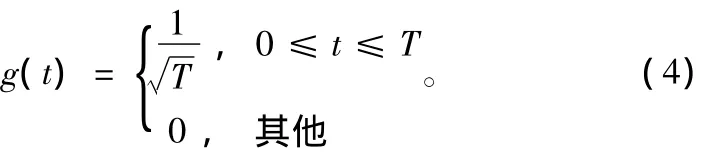
引入时钟抖动τ后的信号表示为:

经过数字下变频后信号表示为:
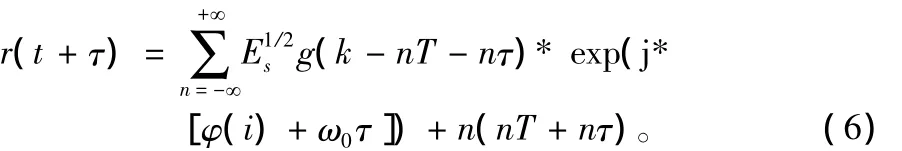
推导中假设时钟抖动方差满足στ<1,此时,

则式(7)可以近似表示为:
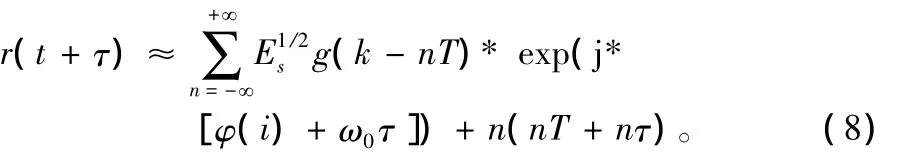
接收端载波恢复后的信号表示为:
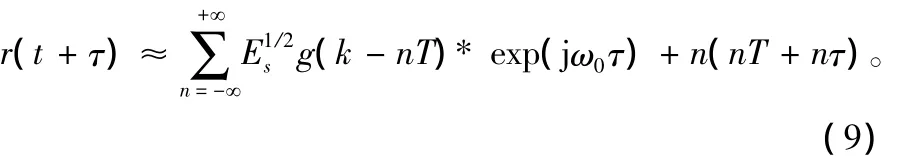
文献[2]和文献[3]推导出相位噪声对 B PSK和QPSK系统误比特率的影响。对于不同的调制方式,由时钟抖动导致的码间串扰量是相同的,而采样时钟抖动产生的载波相位噪声对系统误码率的影响是不同的。令θ=ω0τ,则判决时信号的相位不再是最初的调制相位,而是φ(i)+θ=φ(i)+ω0τ。带通采样时钟抖动对系统的影响除了会带来相位噪声之外还会影响信号的判决,对高阶调制的影响更大。时钟抖动对系统解调信噪比的影响很难进行理论的推导,下面重点通过仿真来说明。
因为时钟抖动的随机性和不确定性,假设时钟沿抖动τ满足均值为0,方差为的高斯分布,对于ωτ满足均值为0,方差为ω2的高斯分布,下面仿真中用相位均方抖动方差来表示 ω2,即=ω2,此时有如下关系:
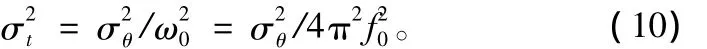
在此定义归一化的时钟抖动,将采样时钟抖动归一化到中频频率可以得出,归一化的时钟抖动为f0τ,方差为。衡量采样时钟抖动对不同调制系统的影响时用归一化的时钟抖动来衡量。
3 仿真验证
3.1 建立仿真模型
带通采样时钟抖动对系统误码率性能的影响仿真模型如图1所示。仿真条件为:成形滤波器和匹配滤波器均采用滚降系数为0.9的平方根升余弦滚降滤波器,在不同的调制方式下相位均方抖动方差取不同的值进行系统误码率仿真,调制方式分别为BPSK、QPSK,仿真长度5 000,仿真次数1 000。仿真中,中频频点f0是可变的。
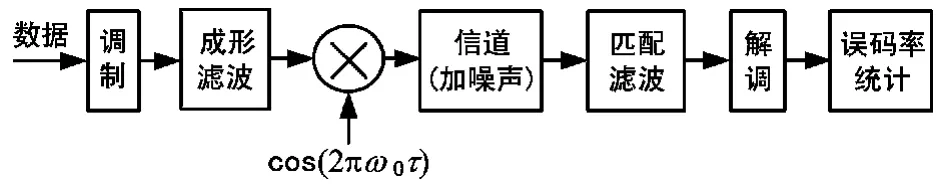
图1 带通采样时钟抖动对系统性能的影响
3.2 仿真1结果及分析

图2 带通采样时钟抖动BPSK系统的误码率影响
3.3 仿真2结果及分析
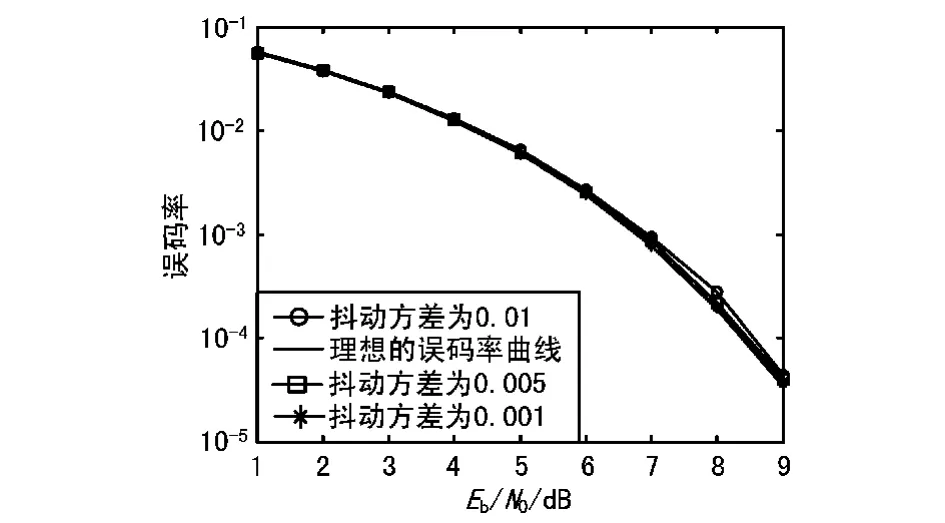
图3 带通采样时钟抖动QPSK系统的误码率影响
3.4 仿真3结果及分析
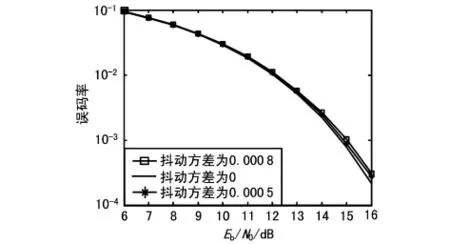
图4 带通采样时钟抖动8PSK系统的误码率影响
信噪比越高,采样时钟抖动对系统的信噪比影响越大。在不同调制方式下对系统性能的影响也不相同,在MPSK调制系统中,相同的采样时钟抖动方差的条件下,M值越大,采样点抖动对其性能的影响也越大。同时,随着中频信号频率的增大,采样时钟抖动对该系统性能的影响也越大。
4 结束语
数字化中频接收系统中带通采样时钟的抖动对系统解调信噪比性能的影响是不容忽视的。具体在某种调制方式下对某个频率的中频信号进行采样时允许的时钟抖动方差可以推过式(10)计算得出。
[1]D ADALT N,HARTENECK M,SANDNR H,.On the Jitter Requirements of the Sampling Clock for Analog-to-digital Converters.IEEE Transactions on Circuits and Systems I,2002,49(9):1 354 -1 360.
[2]杨小军.陈 曦 ,张庆民.时钟抖动对ADC变换性能影响的仿真与研究[J].中国科学技术大学学报,2005,35(1):66-73.
[3]张俊杰,乔 崇 ,刘尉悦.高速数据采集系统时钟抖动研究[J].中国科学技术大学学报,2005,35(2):227-231.

