常规弹药转速测量时频分析方法研究*

尚剑宇，张晓明，2* ，黄建林，崔 星，刘 俊，2

(1.中北大学电子测试技术重点实验室，太原030051;2.中北大学仪器科学与动态测试教育部重点实验室，太原030051)

常规弹药制导化是当今常规弹药发展的主流方向之一［1］。高速旋转可以保证灵巧弹药稳定飞行，因此获得弹丸转速信息是对常规弹药进行改造的必由之路［2－4］。磁传感器通过测量地磁场矢量信息，可完成常规弹丸转速的测量［5－6］，且由于其封装体积小、抗过载能力强、量程大、成本低而脱颖而出。磁传感器用于测量高速旋转弹丸的转速时，会输出频率缓慢变化的非平稳信号，采用一定的时频分析方法分析该信号即可得到弹丸的转速。本文分别采用峰值检测、过零周期检测、短时傅立叶变换(STFT)和“滑动窗口”Chirp-z变换方法对磁传感器输出信号进行时频分析，对比获得精度较高的转速提取算法。

1 常规弹药转速测量原理

磁传感器主要通过敏感地磁场矢量信息来确定弹丸任意时刻的姿态角，且由于其启动时间短，无积累误差而被广泛应用于弹体的姿态测量［7］。本文将单轴磁传感器敏感轴沿弹丸径向安装，通过对弹丸质点外弹道模型、载体磁场模型和单轴磁传感器模型的构建来仿真磁传感器输出信号。由于磁传感器捷联在弹体上，会输出与转速同频率的信号，采用一定的时频分析方法提取磁传感器输出信号的频率即可获得弹丸转速。

为了对该转速提取算法进行评估，需要弹丸理论转速作为参考标准。采用柔格里半经验公式可获得旋转弹丸在外弹道阶段的自转角速度衰减规律［8］，即弹丸理论转速。将上述实验转速和理论转速做误差分析，可得到磁传感器测量弹丸转速的精度。若采用不同的时频分析方法提取信号频率，通过做算法评估还可比较不同时频分析算法的优劣性。

2 磁传感器输出信号频率提取方法

采用一定的时频分析方法分析磁传感器输出信号即可得到信号的时频信息。时频分析［9－11］包括时域分析和频域分析，本文针对磁传感器输出信号，分别对其采用时域分析方法、频域分析方法进行频率提取。

2.1 信号的时域分析

信号的时域处理又称为波形分析，主要是对时域信号波形的分析处理。峰值检测和过零周期检测等方法即建立在时域分析的基础上。

当信号采样率较低或者存在噪声时，通过“峰值检测法”检测出的峰值点有时并不是真实峰值。因此，峰值检测法有一定的局限性，若要提高其精度，需提高信号信噪比和采样率;过零周期检测精度较峰值检测高，但也存在诸如易受噪声影响、采样率低且存在零点偏置的问题。

时域分析方法算法简单、实时性较强，但是易受噪声影响、且采样率较低。因此，时域分析方法较适用于信号的实时分析。若要提高信号分析精度，应当考虑采用频域分析方法。

2.2 信号的频域分析

频域分析是建立在傅立叶变换基础上的时频变换，所得结果是以频率为变量的函数。频域处理的主要的方法为傅立叶变换［12］，后来在傅立叶变换的基础上发展了短时傅立叶变换、Chirp-z变换等频域分析方法。

(1)短时傅立叶变换(STFT)

针对标准傅立叶变换只在频域有局部分析的能力，而在时域内不存在局部分析的能力，加窗傅立叶变换分析方法(短时傅立叶变换)应运而生。通过适当加窗函数的选取，可以实现一定程度上的局部时间分析［13］。

由于短时傅立叶变换实质上是加窗的傅立叶变换，而傅立叶变换其本身的频率分辨率较低，因此，短时傅立叶变换的精度也较低。为了得到更好的效果，应当考虑采用更为适合的频域分析方法。

(2)“滑动窗口”Chirp-z变换

线性调频Z变换(Chirp Z-transform，CZT)是由傅立叶变换导出的一种频谱分析方法［14］，该方法可对信号宽带中的部分频带进行高频率分辨率的频谱细化分析，提高频率分辨率［15］。由于CZT变换本质是一种频域分析方法，分析频率慢变信号时，不能直接得到信号的时频关系。根据短时傅立叶变换是在传统傅立叶变换的基础上加一窗函数［13］的思想，本文引入“滑动窗口”Chirp-z变换细化频率分析方法。“滑动窗口”细化频率分析法如图1所示如下。

图1 “滑动窗口”分析法原理示意图

首先，选取信号中(t1～t2)时间段作为第一个“窗口”，对此窗口内所包含的数据点进行Chirp-z变换分析，得到一个频率值，并认为此数值为该窗口中间时间点的频率值;而后将第一个“窗口”沿时间轴向右滑动Δt，再次选取时间宽度为(t1～t2)的第二个“窗口”分析;以此类推将信号中所有数据分析一遍，即可得到该信号的时间－频率对应关系。

“滑动窗口”Chirp-z变换算法体现出一种局部放大的小波处理思想［13］，能在增加有限计算量的基础上极大地提高频谱分辨率，从而提高测频精度。

频域分析方法不易受噪声和零点偏置的影响，并且其采样率较高，可以有效地解决时域分析方法的缺点，但由于其实时性较差，适用于事后信号分析处理。

3 MATLAB仿真分析

本文分别采用峰值检测、过零周期检测、短时傅立叶变换和“滑动窗口”Chirp-z变换分析一组仿真的单轴磁传感器输出信号，单轴磁传感器敏感轴沿弹丸径向安装。该信号的采样频率为1 000，出炮口转速为50 r/s。

图2为弹丸按照上述初始条件飞行后磁传感器的输出信号。该信号是一条类正弦曲线，其幅值先逐渐增大，后开始减小，减小到一定程度后由于飞行轨迹达到终点而停止。

图3是采用柔格里半经验公式求解出的弹丸理论转速，从初始的50 r/s线性衰减到48.6 r/s。

图2 磁传感器输出信号及其细节

图3 柔格里半经验公式推算出的弹丸理论转速

3.1 峰值检测

图4是通过“峰值检测”方法求解出的弹丸转速实验值(曲线2)和柔格里半经验公式求解出的弹丸转速理论值(曲线1)的对比图;图5为将弹丸转速实验值同理论值做误差分析后得到的转速绝对误差曲线，其转速绝对误差标准差为16.3585°/s。误差较大，究其原因是当信号采样率较低或者存在噪声时，检测出的峰值点有时并不是真实峰值。因此，峰值检测有一定的局限性，若要提高其精度，需提高信号的信噪比和采样率。

图4 弹丸转速实验值和理论值对比图

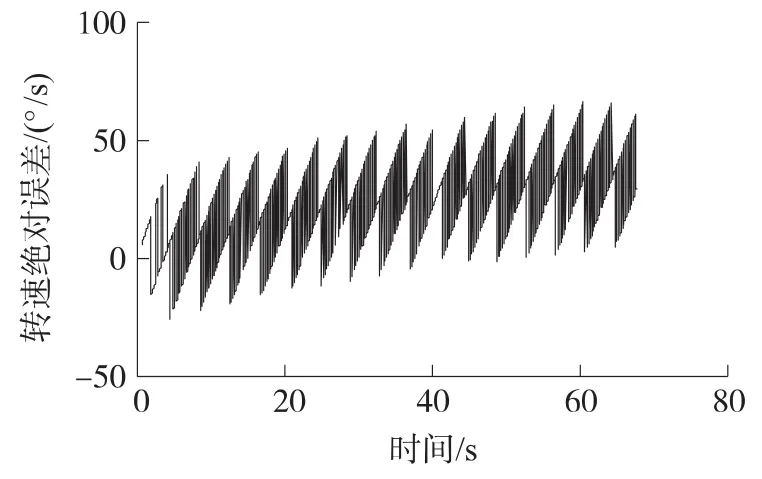
图5 弹丸转速绝对误差曲线

3.2 过零周期检测

图6是通过“过零周期检测”方法求解出的弹丸转速实验值(曲线2)和柔格里半经验公式求解出的弹丸转速理论值(曲线1)的对比图;通过“过零周期检测”算法求解出的弹丸转速误差标准差为1.0417°/s，较峰值检测小。

图6 弹丸转速实验值和理论值对比图

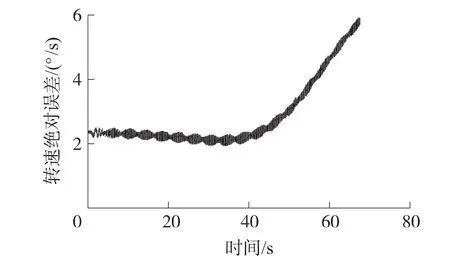
图7 弹丸转速绝对误差曲线

3.3 短时傅立叶变换(STFT)

利用短时傅立叶变换分析信号时，首先获得磁传感器输出信号的STFT时频谱图，见图8;再提取该时频谱图的时频脊线，即可得到信号的时频关系，见图9。图9中曲线2为通过“短时傅立叶变换”方法求解出的弹丸转速实验值，曲线1为柔格里半经验公式求解出的弹丸转速理论值。

图8 短时傅立叶变换分析信号的时频谱图

由短时傅立叶变换求解出的转速绝对误差标准差为515.9449°/s。此误差特别大，究其原因是短时傅立叶变换实质上是加窗的傅立叶变换，而傅立叶变换其本身的频率分辨率较低，实现不了频率的局部化分析。

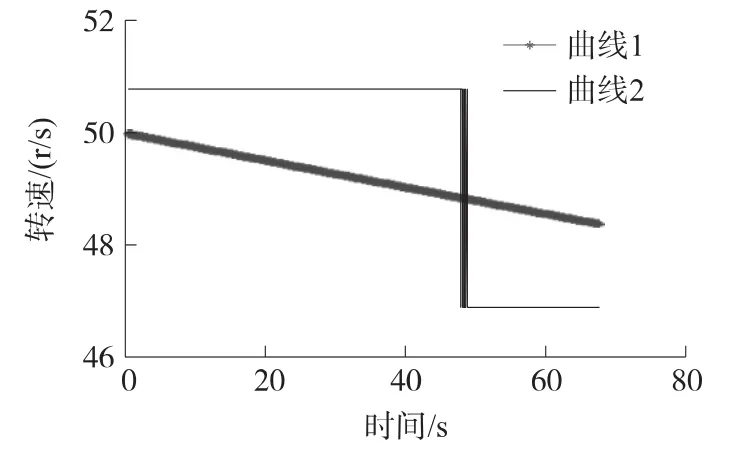
图9 弹丸转速实验值和理论值对比图

图10 弹丸转速绝对误差曲线

3.4 “滑动窗口”Chirp-z变换

图11是通过“滑动窗口”Chirp-z变换方法求解出的弹丸转速实验值(曲线2)和柔格里半经验公式求解出的弹丸转速理论值(曲线1)的对比图;运用“滑动窗口”Chirp-z变换算法求得的转速绝对误差标准差为 0.8755°/s。

图11 弹丸转速实验值和理论值对比图

图12 弹丸转速绝对误差曲线

4 “滑动窗口”宽度对时频分析精度的影响

通过以上四种方法的对比分析，“滑动窗口”Chirp-z变换算法用于提取弹丸转速时误差最小。

以上采用该算法提取信号频率时，“滑动窗口”宽度为25个周期的时间点。研究表明，窗口宽度与频率分辨率和时间分辨率有直接的联系。因此，本文将研究“滑动窗口”宽度对该算法在时域和频域上的影响。

图13为针对上一节的仿真初始条件，采用不同“滑动窗口”宽度时得到的频域和时域误差曲线。可见，随着“滑动窗口”宽度的增加，频域误差逐渐减小，时域误差增大。

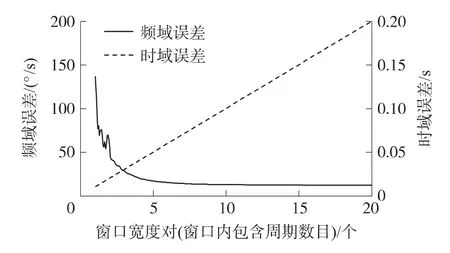
图13 窗口宽度对“滑动窗口”Chirp-z变换算法在频域和时域上的影响

当“滑动窗口”宽度小于两个周期时，频域误差受“所选窗口是否为整周期”的影响较大，并呈现波动性;当“滑动窗口”窗口宽度为2～5个周期时，频域误差受“所选窗口是否为整周期”的影响逐渐减小，且波动性变得不明显;当“滑动窗口”宽度超过5个周期后，窗口宽度的提高对频域误差的减小没有影响，此时的频域误差基本稳定。

可见，随着“滑动窗口”宽度的增加，频域误差逐渐减小，但时域误差逐渐增大。根据Heisenberg测不准原理［13］，时频分辨率在时域和频域上不能同时达到高精度。因此，在保证实时性的基础上，应该尽量加宽“滑动窗口”的宽度，以下将研究在确保实时性的基础上，最佳“滑动窗口”的宽度。

图13中，当时域误差处在0.02 s～0.05 s时，满足频域误差较小、波动不明显所对应的窗口宽度为(2.15～5)个周期。为了验证此结论的普遍性，以下仿真另外八组数据，研究最佳“滑动窗口”的宽度取值范围，其中时域误差范围:0.02 s～0.05 s，结果见下表1。

由表1可知，当满足时域误差要求时，窗口宽度大约从2.2个周期开始。因此，在运用“滑动窗口”Chirp-z变换算法时，窗口宽度应根据具体要求来选定，实时性要求不高时，应适当加宽窗口宽度来增加频率分辨率;如果实时性要求较高，窗口宽度应当尽量短，但最短不应短于两个周期。

表1 时域误差为0.02 s～0.05 s时的最佳“滑动窗口”宽度

5 信噪比(SNR)对“滑动窗口”Chirp-z变换算法做时频分析精度的影响

信号幅值的变化会导致信噪比的变化，为了研究信噪比对“滑动窗口”Chirp-z算法做时频分析精度的影响，仿真一组如图14的磁传感器输出信号，此信号的幅值变化较图3中的更加剧烈。叠加的噪声均值为0，方差为100 nT。

图14 磁传感器输出信号

图15中曲线1和曲线2分别是柔格里半经验公式求解出的弹丸转速理论值和通过“滑动窗口”Chirp-z变换方法求解出的弹丸转速实验值。

图15 弹丸转速实验值和理论值对比图

采用“滑动窗口”Chirp-z算法分析该信号，得到信号的时间－信噪比、时间－转速绝对误差关系如图16和17所示。根据上一节的结论，选定“滑动窗口”的宽度为5个周期，得到的转速绝对误差标准差为 12.4078°/s。

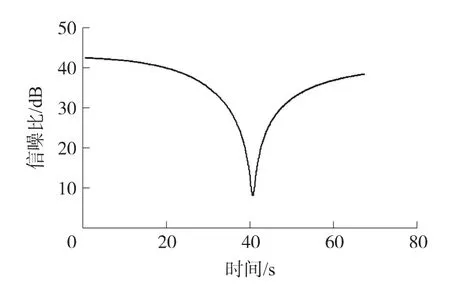
图16 信噪比曲线

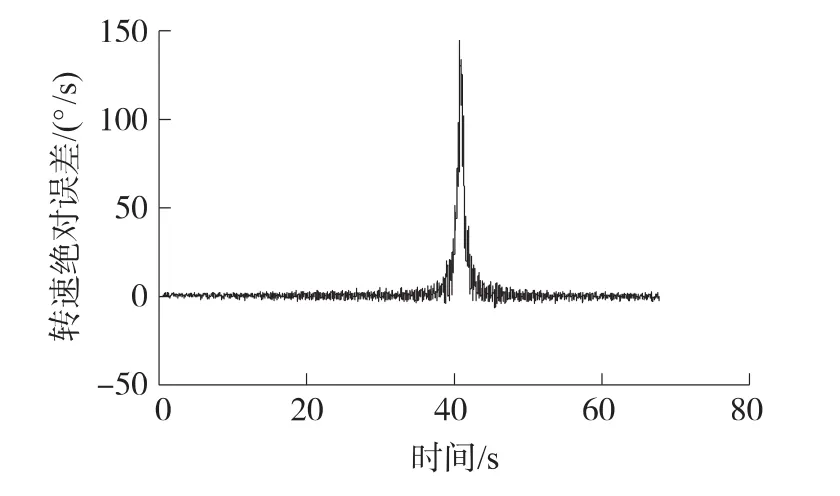
图17 弹丸转速绝对误差曲线

图16中，原始信号的幅值先是减小而后逐渐增大，信噪比SNR也按此规律分布。图17中，磁传感器输出信号幅值在40 s附近急剧减小，此时信噪比也达到最小值，“滑动窗口”Chirp-z算法在此处分析的误差达到最大。

图18为信噪比对“滑动窗口”Chirp-z变换算法做时频分析精度影响的曲线。随着信噪比的增加，转速绝对误差呈减小的趋势。

图18 信噪比对“滑动窗口”Chirp-z变换算法分析弹丸转速的误差影响

因此，针对噪声能量较大的信号，采用“滑动窗口”Chirp-z变换算法做时频分析时精度较低，此时应适当增加“滑动窗口”的宽度来提高算法分析精度。

5 结论

本文提出一种“滑动窗口”Chirp-z变换算法用于提取磁传感器输出信号的频率，进而得到弹丸转速信息。通过将其与其他时频分析方法比较，得出其用于提取弹丸转速时精度最高，且其不易受噪声影响。此外，还有以下结论:①窗口宽度会影响“滑动窗口”Chirp-z变换算法的精度。窗口宽度越宽，频率分辨率越好，但时间分辨率降低;窗口宽度越窄，时间分辨率越好、实时性加强，但频率分辨率降低。无论实时性要求多高，“滑动窗口”的宽度至少应包含两个周期以上的时间点;②信噪比(SNR)对“滑动窗口”Chirp-z变换算法精度有影响。研究表明:信噪比越大，该算法分析信号的精度越高。因此，当信号中噪声能量较大时，需适当加宽“滑动窗口”的宽度，通过牺牲一部分时间分辨率来换取频率分辨率。

［1］ 高峰，张合.基于基准角和补偿角的常规弹药滚转角磁探测算法研究［J］.探测与控制学报，2008，30(5):11－15.

［2］ 黄吉传，刘占辰，房振生.高速旋转弹丸外弹道仿真研究［J］.微计算机信息，2008，24(6):227－229.

［3］ 刘汉忠，顾晓辉.灵巧弹药半实物仿真系统及模型［J］.火力与指挥控制，2005，30(1):55－58.

［4］ 张斌.基于灵巧弹药的目标探测与弹道修正技术研究［D］.太原:中北大学硕士学位论文，2010:1－4.

［5］ 娄朝飞，张锐.地磁传感器在自旋导弹惯测组合中的应用研究［J］.航天控制，2008，26(2):41－46.

［6］ 愈卫博，高敏.基于传感器零值输出的旋转弹丸磁航向测量方法［J］.探测与控制学报，2009，31(1):19－22.

［7］ 李玎，卜雄洙.基于非正交磁传感器组合的旋转弹体横滚角测试［J］.兵工学报，2010，31(10):1316－1321.

［8］ 王雨时.旋转弹丸外弹道自转角速度衰减规律半经验公式［J］.探测与控制学报，2003，25(1):1－6.

［9］ Leon Cohen.Time-Frequency Analysis:Theory and applications［M］.New York:Prentice Hall，1995.

［10］孟宗，戴桂平，刘彬.基于EMD时频分析方法的性能研究［J］.传感技术学报，2006，19(4):1029－1032.

［11］ Mallet S.and Hwang L.Singularity detection and processing with wavelet［J］.IEEE Trans on Information，1992，38(2)，617－643.

［12］王济，胡晓.MATLAB在振动信号处理中的应用［M］.北京:中国水利水电出版社，2006:118－120.

［13］焦叙明.时频分析及其在地震资料处理分析中的应用［D］.青岛:中国海洋大学硕士学位论文，2007:15－20.

［14］何昆英，郭虹，刘洛琨等.一种FFT和CZT联合的快速高精度频率估计算法［J］.数字电视与数字视频，2006，8:18－20.

［15］潘银松，李向全，汪瑛等.适用于像素CZT辐射探测器ROIC的高精度 S/H 电路［J］.传感技术学报，2010，23(9):1261－1265.