基于小波多尺度变换的光纤陀螺振动误差分析与补偿*

方 琳，申 冲，陈熙源*

(1.东南大学机械工程学院，南京210096;2.东南大学仪器科学与工程学院，南京210096;3.微惯性仪表与先进导航技术教育部重点实验室，南京210096)

在惯导系统的工作过程中，机械振动是不可避免且长期存在的，作为惯导系统的核心元件，光纤陀螺在振动环境下能否保持高稳定性与高精度成为影响整个惯导系统精度的重要因素。理论上，光纤陀螺的全固态结构以及无旋转部件等特点使得光纤陀螺具有抗振动能力强、稳定性高等优点，但在实际应用过程中，振动引起的光纤环应力变化、器件尾纤振动以及结构的共振等都将引起陀螺误差，进而影响到整个惯导系统的精度。因此，如何消除或减小光纤陀螺的振动误差，已成为光纤陀螺研发人员共同关心的一个问题。

对振动引起的光纤陀螺误差的抑制方法主要有两种，一是物理方法，从光纤陀螺封装或电路结构上进行改进，如采用固胶的方法提高光线环的抗振性能［1］，在有限元分析的基础上对光纤陀螺的结构进行小型化和轻型化设计并优化装配工艺［2］，在光纤环圈中引入“匹配点”以实现四级对称缠绕技术［3］等，这些方法在一定程度上提高了光纤陀螺在振动环境中的输出精度，但由于实际制作工艺及安装等原因，并不能完全消除振动对光纤陀螺性能的影响。因此在物理方法的基础上，还必须引入第二种方法抑制振动引起的误差，即数学分析方法。利用数学方法对振动环境下的光纤陀螺输出信号进行分析，以确定振动对陀螺各误差项的影响并分别进行抑制与补偿。相比物理方法，利用数学方法进行误差分析与补偿在简易性、可操作性上均有明显优势，本文将利用数学方法对光纤陀螺振动误差进行研究。

本文针对某一型号的光纤陀螺在振动环境下的输出信号进行了小波多尺度分析，通过重构低频信号有效抑制了振动造成的光纤陀螺零漂及噪声，随后利用RBF神经网络对振动造成的零偏误差进行了建模及补偿，Allan方差分析结果表明，本文提出的方法能够有效的抑制振动产生的各误差项，提高光纤陀螺在振动环境下的精度。

1 光纤陀螺振动误差模型及分析

1.1 光纤陀螺振动误差的数学描述

为了方便研究，本文主要介绍光纤陀螺的静态特性及其部分指标。在静基座上，如果光纤陀螺的测量轴位于水平面内，则陀螺的输出信号为［4］:

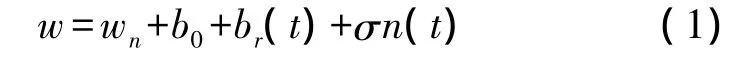
其中，w是光纤陀螺实际输出的角速度信号，wn为真实的角速度信号，b0为陀螺的常值误差项，即零偏，br(t)为陀螺的随机游走，即零漂，σn(t)为零均值的噪声项，σ为方差。其中，零偏和零漂是两个用来衡量光纤陀螺性能的重要指标，其中零偏是指当输入角速率为零时光纤陀螺的输出量，主要反映为低频信号误差，它以规定时间内测得的输出量平均值对应的等效输入角速率表示;零漂为当角速率输入为零时，衡量陀螺输出量围绕其均值的离散程度，主要反映为高频信号误差，以规定时间内输出量的标准差对应的等效输入角速率表示。而噪声如果过大，也会淹没真实信号，影响陀螺精度。本论文将主要针对零偏与零漂及噪声误差进行分析与抑制，以提高光纤陀螺的精度。

1.2 Allan 方差分析

零偏和零漂是衡量光纤陀螺性能的综合指标，包含有很多成分，比如量化噪声(Q)、角度随机游走(N)、零偏稳定性(B)、速率随机游走(K)以及速率斜坡(R)，其功率谱函数可分别表示为:

量化噪声:

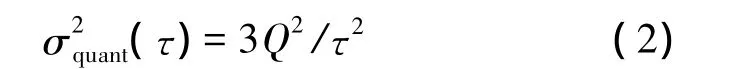
其中Q为量化噪声系数。

角度随机游走:

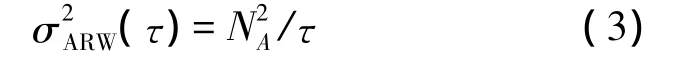
其中NA是速率随机游走系数。

零偏稳定性:

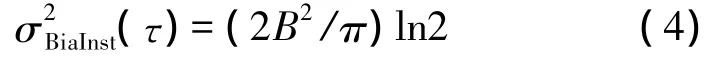
其中B是零偏稳定性系数。

速率随机游走:

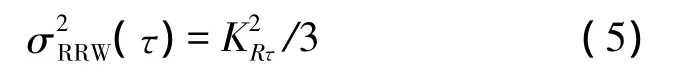
其中KRτ是速率随机游走系数。

速率斜坡:

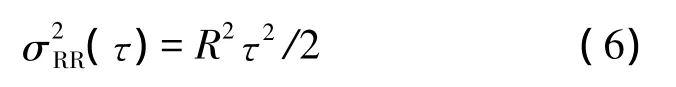
其中R为速率斜坡系数。

在工程上常采用Allan方差分析法来计算这些误差系数。Allan方差分析法［5－6］由美国国家标准局于20世纪60年代提出，是IEEE公认的陀螺仪参数分析的标准方法。

1.3 振动实验与数据分析

针对在加速度值一定的情况下，不同振动频率对光纤陀螺性能的影响，做了两组线振动实验，第一组实验在1 Hz～500 Hz扫频振动下采集了光纤陀螺输出信号，第二组在500 Hz固定频率的振动下采集了光纤陀螺输出信号。两组信号如图1所示。

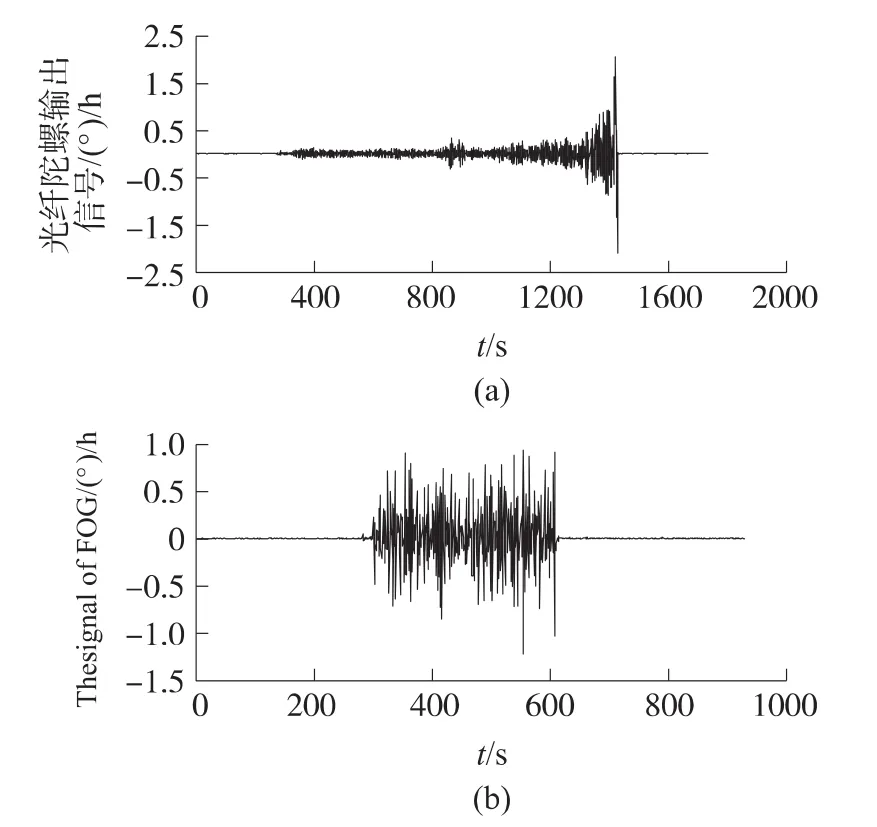
图1 两组振动实验下的光纤陀螺输出信号

在图1中，图1(a)为扫频振动下的光纤陀螺输出信号，图1(b)为固定频率下的光纤陀螺输出信号。由图1可得，两组信号波形均包含三个阶段，第一阶段为未加振动时的陀螺静态输出，第二阶段为加入振动后的陀螺输出信号，第三阶段为取消振动后陀螺的输出信号。以图1(b)信号为例，对三阶段分别进行Allan方差分析，分析结果如表1所示。

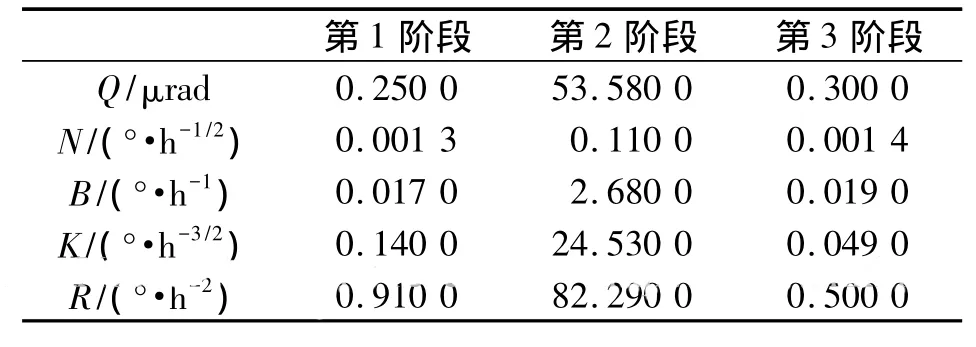
表1 图1(b)中三阶段Allan方差系数对比

由表1可得出以下结论:①相比第1和第3阶段，第2阶段的各误差系数均有显著增加，说明振动下的光纤陀螺输出产生较大误差;②第1和第3阶段相比，量化噪声(Q)、角度随机游走(N)和零偏稳定性(B)基本没有变化，而速率随机游走和速率斜坡均有减小，但相比于第2阶段的变化，该减小并不明显，因此可认为振动前后陀螺精度无明显变化。

2 小波多尺度分析

2.1 小波多尺度分析

为更好的分析并有效消除振动环境下光纤陀螺信号中的误差，本文引入了有“数学显微镜”之称的小波多尺度分析方法［7］。小波多尺度分析在时域、频域都具有良好的局部化性质，目前应用于小波多尺度分析的常见算法为Mallat塔式分解与重构算法，Mallat算法的原理及流程在有关小波的文献中多有详细介绍［8］。与另两种常用的分析方法－频谱分析和EMD变换方法相比，小波分析具有自己的优势。以500 Hz振动下的陀螺信号为例，分别进行频谱分析、EMD变换和小波变换分析，分析结果如图2所示。

图2中，图2(a)为信号的频谱分析图，从图中仅能看出信号在高频段引入了噪声，并且幅值随着频率的增加而增大，但不能得到时域内的频率变化情况;图2(b)为EMD变换的频谱图，从图中可看出该方法并未得到良好的分析结果，因为在信号受到噪声污染时，EMD方法并不能得到良好的分析结果［8］;图2(c)为连续小波变换分析图，从图中可以清晰的看出信号频段随时间的变化情况:第一阶段没有引入振动，第二阶段引入高频振动，以及第三阶段振动消除。从图2(c)可以得到清晰的分析结果，因此本文选取小波方法对振动环境下的陀螺信号进行分析。

母函数的选取是小波分析的关键点，不同的母函数的选取可使相应的小波变换体现不同的信息特征，一般情况下，依据小波母函数的性质，希望选取紧支撑、对称、正则性好以及消失矩高的母函数［7］，但根据Heisenberg测不准原理，严格满足以上要求的函数并不存在。考虑到漂移信号多尺度分解对小波母函数完备性的基本要求，并兼顾局部分析中要求的紧支性与高消失矩等性质，在参阅大量相关参考文献和多次实验的基础上，本文选取db4为小波母函数，并利用Mallat塔式算法进行多尺度分析。

以1 Hz～500 Hz扫频振动下的光纤陀螺输出信号为例，进行尺度为10的小波多尺度变换后的三维时频图如图3所示。

图2 三种频率分析方法的频谱图

图3 扫频振动陀螺信号的三维时频图

由图3可见，分解尺度较低部分，即高频信号存在明显的漂移和噪声分量，分解尺度越高，漂移和噪声分量就越小。从图3还可以明显看出，在分解尺度较高即低频信号部分，相比第一和第三阶段信号，第二阶段即振动部分的信号在高振动频率(约300 Hz～500 Hz)的部分还是存在着一定的偏移误差。对光纤陀螺而言，理想情况下的零偏误差为低频信号，零漂与噪声误差为高频信号，因此在利用小波多尺度分析对信号进行处理的时候，可重构低频逼近信号作为陀螺零偏误差，将高频细节信号进行重构作为零漂误差与噪声项。小波多尺度分解的分解层数选取也是一个关键问题，本文对原始数据进行尺度为10的分解，通过反复比较相邻几层信号的变化趋势，发现第六层逼近信号去除了大量噪声并最大程度的保留了真实信号，因此选取第六层逼近信号作为零偏信号进行重构，对第一层至第六层的细节信号进行重构作为零漂及噪声信号。如图4所示，图4中a7为第七层逼近信号，d6、d1、d分别为第六层、第一层细节信号以及重构后的零漂及噪声信号。对重构后的零偏与零漂及噪声误差分别进行Allan方差分析，对比结果如表2所示。

图4 小波分解后的低频与高频信号

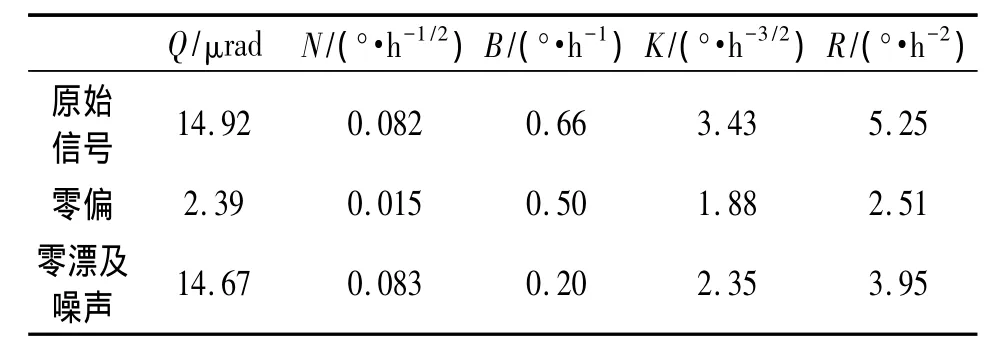
表2 原始信号与重构后的误差项系数对比

由表2可得以下结论:①与原始信号相比，提取的零偏信号的误差系数中量化噪声与角度随机游走和速率斜坡下降较大，与之相比零偏稳定性、速率随机游走下降较小，表明误差系数中的零偏稳定性、速率随机游走主要表征了信号的低频误差即零偏误差;②零漂与噪声信号的误差系数中，量化噪声、角度随机游走和速率斜坡变化很小，而零偏稳定性、速率随机游走下降较大，表明误差系数中的量化噪声、角度随机游走和速率斜坡主要表征了信号高频误差即零漂与噪声误差。

从表2中我们还能看出，利用小波多尺度分析可以有效的去除陀螺误差项中的零漂与噪声误差，但是对零偏误差则没有很好的抑制。因此为了抑制零偏误差，还必须建立高精度的零偏误差模型以对其进行补偿。

3 RBF神经网络建模补偿

为抑制零偏误差带来的影响，本文使用径向基函数(RBF)神经网络建立关于振动频率与光纤陀螺零偏误差的关系模型，以实现依据振动频率对零偏误差进行补偿。RBF神经网络由于其可以逼近任意函数的能力和训练速度快等优点而被广泛应用到建模、预测以及故障诊断中来［9－11］。其具体工作原理可参见文献［12］。一个典型的RBF神经网络结构如图5所示。

图5 RBF神经网络结构图

在本文中，以1 Hz～500 Hz的振动频率为输入，以对图4中a7重构后得到的零偏误差为输出建立了单输入单输出的RBF神经网络模型进行逼近。训练时，选取网络训练的目标精度为0.000 1，经过多次验证发现散布常数选为1.2时逼近效果较为理想，网络中心的选择方式为随机固定法。与传统的最小二乘拟合逼近方法相比，RBF神经网络的逼近精度更高，建立的模型更准确。RBF神经网络逼近结果与最小二乘拟合逼近结果的对比如图6所示。

图6中，蓝线为陀螺零偏曲线，红线为RBF神经网络逼近曲线，绿线为4阶最小二乘拟合逼近曲线。可见RBF神经网络的逼近精度远高于最小二乘拟合方法的逼近精度。图7为利用小波多尺度变换后去除零漂与噪声误差信号的曲线图，蓝线为500 Hz振动频率下的陀螺信号，红线为去零漂及噪声后的信号，可得在振动阶段，去除零漂及噪声后的信号还是存在一定的偏移，即零偏误差，该误差在图8中反映的较为明显。图8为利用RBF神经网络所建立的逼近模型对500 Hz振动所产生的零偏误差进行补偿，图中的蓝线对应图7中的零偏误差信号，可以看出振动阶段存在较大的偏移误差，红线为补偿后的信号，可见除振动边界处有较大波动外，振动过程中的零偏误差已得到良好的补偿。这一过程的Allan方差分析结果如表3所示。

图6 两种方法的逼近曲线对比

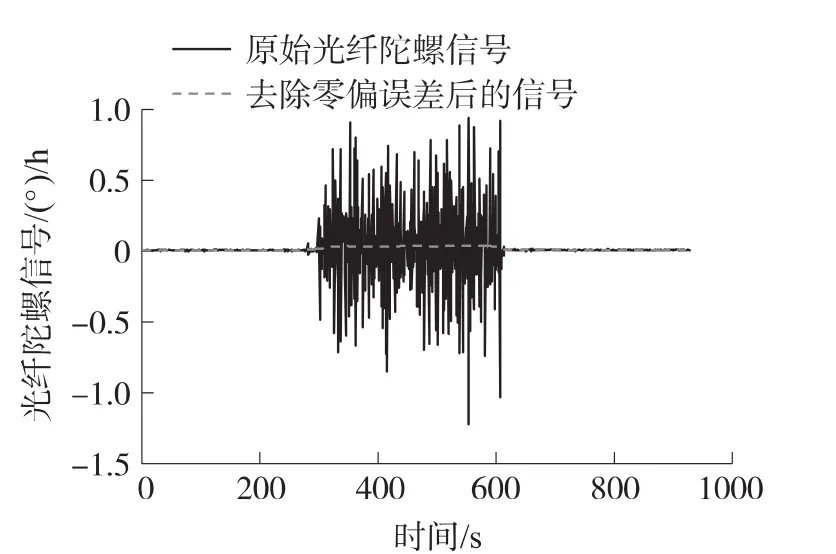
图7 去零漂及噪声信号曲线图

图8 零偏误差补偿曲线图

表3 补偿结果的Allan方差分析

由表3可得，在去零漂及噪声误差后，表征零漂及噪声误差的量化噪声与角度随机游走两误差系数明显减小，随后用RBF建模及最小二乘拟合建模分别进行零偏误差补偿，可见表征零偏误差的零偏稳定性、速率随机游走和速率斜坡三项误差系数均明显下降，但RBF建模补偿后的误差系数明显小于最小二乘拟合建模补偿后的误差系数，说明利用RBF神经网络建模精度更高，能更有效地消除光纤陀螺信号中的零偏误差。

4 结论

本文针对线振动环境对光纤陀螺性能的影响，利用小波多尺度变换对光纤陀螺在振动环境下的信号进行了分析，建立了基于RBF神经网络的光纤陀螺零偏误差模型并进行了补偿，对仿真结果进行了Allan方差分析，得到以下结论:①振动前后光纤陀螺的性能未发生明显变化;②小波多尺度分析能够提取出振动环境下光纤陀螺信号中的各误差项并对零漂及噪声误差进行有效的抑制;③光纤陀螺误差项中的零漂与噪声误差与Allan方差分析误差系数中的量化噪声、角度随机游走及速率斜坡相对应，零偏误差与零偏稳定性、速率随机游走相对应;④利用RBF神经网络建立精确的零偏误差模型并进行补偿，该方法优于传统的最小二乘拟合方法，有效降低了Allan方差分析中的各误差系数，提高了振动环境下光纤陀螺的工作精度。

［1］ 孟照魁，邵洪峰，徐宏杰，等.固胶对保偏光纤环的影响［J］.北京航空航天大学学报，2006，32(8):958－961.

［2］ 刘颖，李言，徐金涛.光纤陀螺动力学特性研究及结构优化设计［J］.红外与激光工程，2009，38(3):520－524.

［3］ 吴衍记，黄显林.机械振动对光纤陀螺的影响及其减小措施［J］.红外与激光工程，2008，37(2):363－365.

［4］ 袁瑞铭，孙枫，陈慧.光纤陀螺信号的小波滤波方法研究［J］.哈尔滨工业大学学报，2004，36(9):1235－1238.

［5］ David A Howe，Donald B Percival.Wavelet Variance，Allan Variance，and Leakage［J］.IEEE Transactions on Instrumentation and Measurement，1995，44(2):94－97.

［6］ 姬伟，李奇.光纤陀螺信号误差分析与滤波算法的研究［J］.传感技术学报，2007，20(4):847－852.

［7］ 蒋庆先，吴富梅.基于小波阈值消噪的光纤陀螺信号的抗差估计［J］.传感技术学报，2009，22(11):1596－1601.

［8］ 孙亮，侯宏.阻尼识别的小波和EMD方法仿真对比研究［J］.振动、测试与诊断，2008，28(2):164－167.

［9］ 王璐，潘紫薇，叶金杰.基于EKF训练的RBF神经网络及其故障诊断应用［J］.振动、测试与诊断，2008，28(4):358－361.

［10］林海军，杨进宝，汪鲁才，等.基于复合RBFNN的数字温度传感器误差补偿方法［J］.传感技术学报，2011，24(2):243－247.

［11］张小俊，张明路，李小慧.基于RBF神经网络的电化学CO气体传感器的温度补偿［J］.传感技术学报，2009，22(1):11－14.

［12］ Chen Xiyuan，Shen Chong，Xu Changyan.Application of Filtering Fusion for FOG Based on Improved RBF Neural Network［J］.ICIC Express letters，2009，3(3):847－852.