一种宽频被动雷达制导信号的鲁棒滤波方法

程雪梅 杨俊鹏

西北工业大学，西安 710072

一种宽频被动雷达制导信号的鲁棒滤波方法

程雪梅 杨俊鹏

西北工业大学，西安 710072

探索提高制导武器末制导系统抗噪声扰动鲁棒性的技术方法，研究了一种能将制导信号不确定噪声引起的滤波估计误差控制在一定边界范围内的鲁棒滤波算法，采用该算法对宽频被动雷达导引头测量输出信息滤波估计，可以弱化不确定随机噪声对制导系统的扰动，从而提高制导系统抗噪声扰动的鲁棒性。通过仿真验证了算法的有效性。

制导信息;不确定噪声;鲁棒滤波;估计误差

在反辐射制导武器中，被动雷达导引信号的测量误差是影响制导精度的主要因素，尤其是宽频段被动雷达头对工作频率较低和较高频点的测量信噪比低，而且这种测量噪声随雷达频点、地形等影响的随机性大，致使制导精度降低。对于这种具有较强不确定性的噪声，经典卡尔曼滤波方法无法得到满意效果。因此，本文将鲁棒控制思想引入滤波器设计中，设计一种宽频被动雷达制导信号的鲁棒滤波方法，能将系统不确定噪声引起的滤波估计误差控制在一定边界范围内，弱化不确定随机噪声对制导系统的扰动，从而提高制导系统抗噪声扰动的鲁棒性。通过仿真验证了算法的有效性。

1 鲁棒制导滤波器设计

被动雷达导引头按纵向和侧向两个制导平面输出目标视线角和目标视线角速度作为制导信号，而在目标视线角和目标视线角速度测量输出中包含不希望的不确定随机噪声，需要设计制导滤波器进行滤波处理。本文为了简化描述而又不失说明问题，仅考虑了纵向目标视线角和角速度的滤波器设计。

首先在发射坐标系中建立目标视线角和目标视线角速度数学模型。发射坐标系为惯性坐标系，坐标原点o取在制导武器的发射点，ox轴水平并指向制导武器发射方向，oy轴垂直于水平面指向上。在oxy坐标平面内，制导武器与目标的相对运动关系如图 1 所示［1］。

图1 制导武器与目标相对运动关系图

以xT，yT和xm，ym分别表示目标和制导武器的位置坐标，制导武器在ox轴和oy轴的加速度分量为amx，amy。假设目标运动规律可以用一阶辛格模型表示，那么制导武器与目标相对运动模型可以表示为如下矩阵形式:

其中

方程中，γTx，γTy为一阶相关时间常数，wx，wy为高斯白噪声，x=［x1x2x3x4x5x6］T为制导武器和目标的相对位置、相对速度以及相对加速度。那么目标视线角η和视线角速度q可以由相对位置x1，x2以及相对速度x3，x4计算得到。以 z=［ηq］T表示导引头输出的制导信号向量，则制导信号的测量方程可表示为:

上式中，v=［v1v2］T为制导信号测量噪声。

将方程(1)和(2)离散化，则得到离散形式为:

其中，wk，vk为零均值白噪声，其方差分别为Q和R［2］。

将测量方程(4)线性化得到

根据方程(3)，(6)可以得到系统扰动噪声wk到滤波残差相关量Hkxk，Δkxk的传递函数矩阵分别为:

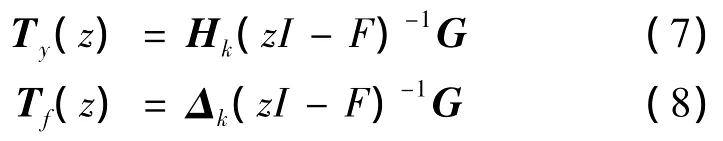
从而得到系统扰动噪声wk引起的系统估计误差的传递函数矩阵为［3］:

对于由方程(3)和(9)描述的系统，由于测量噪声的统计特性有较强不确定性，不能满足经典卡尔曼滤波对噪声统计特性的要求，因此会使滤波效果不理想甚至发散。但是如果测量噪声的上界可以统计得到，那么可以构造一个辅助系统，辅助系统和原系统间的关系由下面引理1进行定义。

引理1:给定两个稳定离散系统Σ1，Σ2为

当系统矩阵满足条件

时，则有 Y1(w)≤Y2(w)，Y1(w)，Y2(w)分别为y1，y2的功率谱密度矩阵［4］。

根据引理1，若方程(9)表述的传递函数可确定边界值，那么可将不确定系统转化为具有确定边界的辅助系统，基于该辅助系统设计卡尔曼滤波器可以得到该系统状态的无偏估计。由于该辅助系统相对于原标称系统补偿了不确定性的影响，因此基于该系统设计的卡尔曼滤波器对原标称系统具有一定的鲁棒性，即在系统的不确定性影响下，该滤波器的估计误差控制在一定范围内。

如果传递函数Tf有一上界Tu，那么可以根据系统噪声wk输出的功率谱密度推导确定该上界值。定义存在以Tu为上界的系统为

用Tuxk替代Δxk，并且将系统Tu加入到方程(3)和(6)中，得到

基于系统(12)进行卡尔曼滤波设计。假设k时刻 ξk的估值为 ξk|k，方差为 P，在k+1 时刻测量得到zk+1，ξk的估值通过以下步骤得到:

1)预测

2)新息

3)更新

根据引理1可以得到该滤波算法对原系统具有一定的鲁棒性，估计误差可以控制在确定的范围内。

2 仿真

某反辐射武器制导系统以被动雷达导引头测量输出的目标视线角速度作为制导信号，采用比例导引进行末段制导。设定导引头测量噪声服从N(0，0．8)的正态分布特性。图2给出了制导武器对地面目标攻击过程中目标视线角速度的变化曲线。在0.6～1.0s时间段内，噪声引起导引头目标视线角速度扰动幅值达60(°)/s。图3给出了采用常规卡尔曼滤波给出的滤波估计结果，可以看到，虽然噪声扰动时间短还未引起滤波发散，但对噪声扰动的滤波效果十分不理想，这对攻击精度的影响是致命的。图4给出了采用本文设计的鲁棒滤波算法对噪声扰动的滤波效果，其将噪声扰动弱化到了制导系统要求的精度范围内，达到了预期目的，提高了制导系统抗噪声扰动的鲁棒性。

图4 目标视线角速度鲁棒卡尔曼滤波估计输出

3 结论

本文研究了一种用于宽频被动雷达制导信号的鲁棒卡尔曼滤波算法，它将系统中未建模高频动态特性以及外部扰动等可能的不确定因素以当量噪声的形式引入到标称状态中，滤波算法设计基于引入噪声后的系统状态，从而在设计过程中对不确定因素进行了预补偿，使滤波算法对制导信号中包含的不确定噪声具有鲁棒性。通过仿真分析表明该算法的有效性。

［1］周荻.寻的导弹新型导引规律［M］.北京:国防工业出版社，2002.

［2］Hassibi.B.，Kailath T.，Sayed A.H.Array Algorithms for H∞Estimation［J］.IEEE Trans Automatic Control，2000，45(4):702-706.

［3］U.Shaked.H∞Minimum Error State Estimation of Linear Stationary Process［J］.IEEE Trans.Automatic Control，1990，35(5):554-557.

［4］H.K.Winmmer.Extensions of the Bounded Real Lemma of Discrete Time［J］.Systems.Int.J.Control，2000，73(14):1322-1328.

The Robust Filter Design for the Guidance Signal of Wide-band Passive Radar Guided Weapon

CHENG XuemeiYANG Junpeng
Northwestern Polytechnical University，Xi’an 710072

The technologies of improving guidance system robustness of guided weapon are researched．A robust filter method that can make the estimation errors induced by an uncertain bound is studied．By using the proposed method to filter the output measurement information of the seeker，a guided weapon guidance system is more robust when some uncertain noises occur．The validity is proven by simulation．

Guidance information;Uncertain noise;Robust filter;Estimation error

TP273

A

1006-3242(2012)01-0003-03

2011-03-30

程雪梅(1972-)，女，河南南阳人，博士，高级工程师，主要研究领域为无人飞行器控制总体、制导与控制、大系统仿真;杨俊鹏(1976-)，男，西安人，博士，高级工程师，主要研究领域为无人飞行器飞行力学、制导与控制、飞行器系统建模与仿真。