基于排队论的机场末端光电防护红外侦察告警多目标处理能力分析
敖 琪
(国防科技大学,安徽 合肥 230037)
0 引 言
光电制导武器因其制导精度高、突袭速度快、破坏威胁大等特点,常常被用于现代化精确空袭作战,对飞机、塔台等机场目标和重要设施构成极大的生存威胁,给机场末端光电防护作战侦察告警能力提出了很高要求[1]。在机场末端光电防护作战中,红外侦察告警通常被用于引导激光干扰设备发现目标并实施激光干扰,是重要的侦察手段,必须运用科学方法计算其作战能力及保障需求,以便有效应对处理多批次空袭目标。
1 问题描述
红外侦察告警,即通过发射、接收红外光,对敌方光辐射源或散射源进行探测、搜索、定位、辨别、测定,判断其威胁程度,并实时提供相关情报、发布告警信息而采取的行动。在机场电子防空反精确制导作战中,假定阵地情况足够理想,来袭制导武器多批次、多方向进入,对于某一红外告警器而言,由于其侦察告警容量有限,超过上限将认为设备饱和,不再对后面的来袭制导武器实施侦察告警。可将红外告警器看作一个服务机构,来袭武器的制导过程就是一个制导武器接收告警设备告警服务的过程,为了能够提供足够有用有效的干扰反应时间,确保满足作战需求的红外告警概率,可利用排队服务模型精确计算红外告警服务能力及相关保障需求。
2 模型建立
2.1 系统假设
在反精确制导作战中,红外侦察告警设备在部署阵地等待来袭制导武器光辐射源或散射源的到来,提供侦察告警服务,以便将信号参数传输给激光干扰单元实施干扰行动。以红外侦察告警设备为服务机构,将来袭制导武器光辐射源看作是告警排队系统的“顾客”,从进入告警作用半径开始,接受某一红外侦察告警设备的服务直至防御方对来袭制导武器实施干扰结束[2]。可先研究单个红外侦察告警设备对来袭制导武器提供侦察告警的概率,通过分析告警概率与红外侦察告警设备服务强度、来袭制导武器到达强度等之间的关系,找出改善红外侦察告警能力的有力举措。对红外告警排队系统作如下假设[3]:
一是到达过程。假设来袭制导武器到达红外告警作用半径接收告警服务事件在任意Δt时间内发生的次数是相同的,且到达告警服务系统的时间间隔独立,服从到达强度为λ的负指数分布,其概率密度函数为:
(1)
二是排队规则。被任何来袭制导武器击中都是防护方不愿意承受的,因此可以预设所有来袭制导武器的优先级相同,选择“先来先服务”的排队规则。当来袭制导武器过多时,红外告警设备达到饱和,不能再对后面的来袭制导武器实施侦察告警。
三是服务时间。假设红外告警设备对来袭制导武器的处理服务时间是独立的,服从参数为μ的负指数分布:
(2)
四是逗留时间。来袭制导武器的逗留时间是等待时间与服务时间两者之和,设来袭制导武器的制导时间为tz,从红外侦察告警到实施有效干扰的反应时间为tf,若在tz-tf时间段内没有完成对来袭制导武器的侦察告警,被保护机场目标将被攻击,告警失去意义,因此,来袭制导武器的逗留时间是有限的。
2.2 模型建立
根据以上假设,可选择单服务台混合制排队模型(M/M/1/K),即来袭制导武器的到达时间服从参数为λ的负指数分布,红外告警设备的处理时间服从参数为μ的负指数分布,红外告警设备最多允许K-1个来袭制导武器等待处理,超过K-1个将不再响应[3]。对任意给定的时刻t和足够小的时间增量Δt,在时间区间[t,t+Δt]内可能发生以下情况:
(1) 有1个来袭制导武器到达的概率为λΔt,有1个来袭制导武器被成功告警服务的概率为μΔt;
(2) 在时刻t,有n个来袭制导武器,而在时间区间[t,t+Δt]内,有1个来袭制导武器到达,且有1个来袭制导武器被成功告警服务的概率为λΔt·μΔt;
(3) 在时刻t,有n+1个来袭制导武器,而在时间区间[t,t+Δt]内,没有新的来袭制导武器,但有1个来袭制导武器被成功告警服务的概率为(1-λΔt)·μΔt;
(4) 在时刻t,有n-1个来袭制导武器,而在时间区间[t,t+Δt]内,有1个来袭制导武器到来,而没有1个来袭制导武器被完成告警服务的概率为λΔt·(1-μΔt);
假设在时刻t+Δt恰有n个来袭制导武器的概率为Pn(t+Δt),由于上述4种情况是相互独立的,即都有可能发生,因此可得:
Pn(t+Δt)=Pn(t)·(1-λΔt)·(1-μΔt)+
Pn(t)·λΔt·μΔt+Pn+1(t)·(1-λΔt)·μΔt+
Pn-1(t)·λΔt·(1-μΔt)
(3)
略去高阶无穷小量(Δt)2,则有:
Pn(t+Δt)=Pn(t)·(1-λΔt-μΔt)+
Pn+1(t)·μΔt+Pn-1(t)·λΔt=Pn(t)+
λPn-1(t)·Δt+μPn+1(t)·Δt-(λ+μ)Pn(t)·Δt
(4)
考虑n=0的情况,在时刻t+Δt没有来袭制导武器排队的状态有2种情况:
(1) 在时刻t,没有来袭制导武器的概率为P0(t),在时间区间Δt内,没有来袭制导武器到达的概率为1-λΔt,在时间区间Δt内,没有来袭制导武器被服务,无需考虑该因素。因此,这种情况发生的概率为P0(t)·(1-λΔt);
(2) 在时刻t,有1个来袭制导武器的概率为P1(t),在时间区间Δt内,没有来袭制导武器到达的概率为1-λΔt,有1个来袭制导武器被服务好的概率为μΔt。因此,这种情况发生的概率为P1(t)·(1-λΔt)·μΔt。
可以得出,在时刻t+Δt没有来袭制导武器排队的概率:
P0(t+Δt)=P0(t)·(1-λΔt)+
P1(t)·(1-λΔt)·μΔt
(5)
略去高阶无穷小量(Δt)2,则有:
P0(t+Δt)=P0(t)-λP0(t)Δt+μP1(t)Δt
(6)
假设红外告警服务系统进入稳定状态情况,则P0(t),…,Pn(t)都与t无关,为常量,导数为0,可得到:
(7)
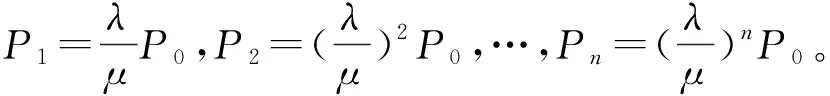
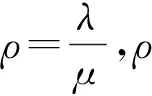
当n=K时:
(8)
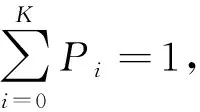
(9)
来袭制导武器平均数(排队长度)为:
(10)
来袭制导武器的逗留时间为:
(11)
3 仿真计算
在某军用永备机场末端光电防护作战行动中,使用红外侦察告警设备实施侦察告警,在不考虑气候条件影响及机场地形条件情况下,假设红外侦察告警设备上限容量K=10,单位时间内能够提供告警服务的平均数μ=10批/min,则未被告警的概率与来袭武器的到达强度λ之间的关系如图1所示。
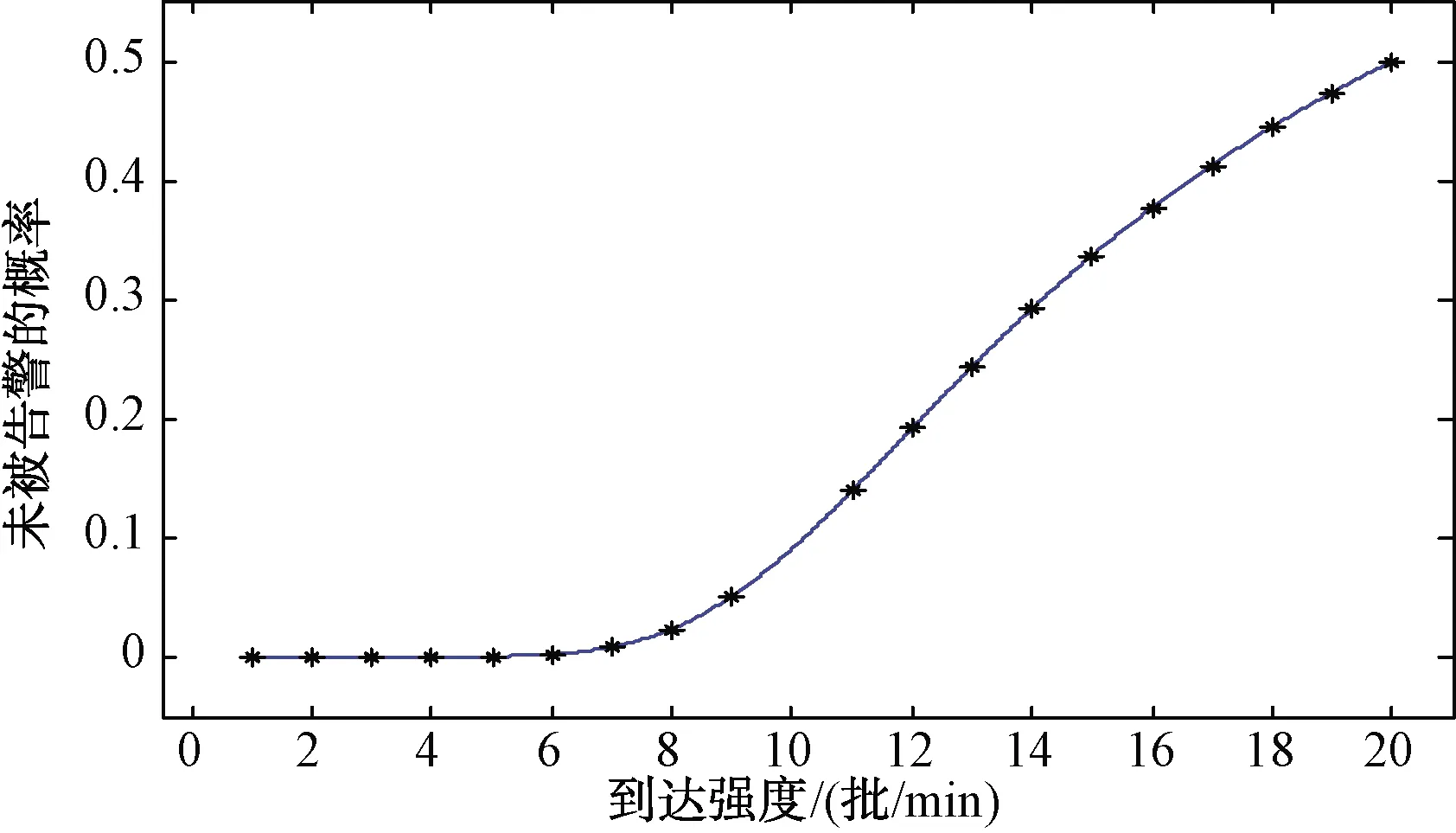
图1 未被告警的概率与来袭武器的到达强度之间的关系
可以看出,当来袭武器的到达强度λ小于6批/min,未被告警的概率几乎为0,但是当到达强度λ增大到20批/min时,近一半的来袭武器未被告警。也就是说,当μ一定时,到达强度λ如果超过一定级别,红外侦察告警设备失去作用,没有组织防护的意义。随着μ的逐步增大,到达强度的上限也可增大,可通过改善红外侦察告警设备的处理信号效率来提高应对高强度多目标能力。
4 结束语
本文基于排队模型研究分析了机场末端光电防护作战行动中的红外侦察告警设备的侦察告警能力,通过比较来袭制导武器强度与红外侦察告警设备失去告警能力之间的关系,得出当来袭制导武器信号的到达强度超过一定值后,红外侦察告警设备将失去告警作用,不得不通过提高其自身处理信号效率来应对高强度多目标处理能力,为研究运用红外侦察告警设备提供了很好的借鉴。

