用同余数表证明哥德巴赫猜想

叶雉鸠

（陕西财经职业技术学院，陕西 咸阳712000）

哥德巴赫（C.Goldbach，1690.3.18—1764.11.20）是德国数学家。1742年，哥德巴赫提出了著名的哥德巴赫猜想（Goldbach Conjecture）——每个不小于6的偶数都可以表示为2个奇素数之和。

1 命题的转换及同余数表

1.1 命题的转换

原命题每个不小于6的偶数都可以表示为2个奇素数之和。

命题0 每个不小于12的偶数都可以表示为2个奇素数之和。

命题0与下列的命题1等价。

命题1 对于任意大于10的偶数2a（a≥5，且a∈N），下列方程组无正整数解。

定义下列3个集合：

命题1的解读，该同余式方程组的特点是：

首先，同余式方程左边的被减项是不大于2a的所有顺序排列的所有奇素数的全集，一个奇素数也不能少。为了确保（1）同余式方程左边的数值不小于3，所以在左边统一加2，这并不影响证明推论的逻辑一致性。（1）也可以理解为：“对于任意大于12的偶数2a＋2（a≥5，且a∈N），方程组（1）无正整数解”。

最后，所谓“方程组（1）无正整数解”的语义可以做以下3层理解：a无正整数解；方程组（1）中的同余式左端差的数值除以相对应模量的商不能全为正整数；方程组（1）中所有的未定数不能同时为正整数，即方程组（1）无解。

命题2 2a（a≥5）以内的所有奇素数，不可能以内的奇素数为模进行同模同余表示。即下列同余式方程组无解。

命题中同余式方程组的要点：

（1）命题中同余式方程组（2）的左边奇素数从上到下按顺序排列，是Pk的全集。

（2）方程组（2）右边不讲究顺序，也不讲究奇素数是否为Pb的奇素数的全体，即可以为Pb的全集，也可以为Pb的子集。

（3）方程组（2）右边讲究模和同余数的对应关系，就是说相同的模对应相同的同余数；不要求同余数相异，即x1，x2，…xb可以相同，也可以不尽相同，也可以完全不同；x1，x2，…xb没有大小顺序，即并不意味着存在x1≤x2≤…≤xb的顺序关系。

根据孙子定理，下式恒有解。

式（3）减去式（1）的对应方程式就会得出式（2）。若式（2）无解成立，则式（1）无解；若式（1）无解成立，则式（2）无解。因此，命题1和命题2为等价命题。

1.2 同余数表

以pb为模的pk同余数表。为了证明命题2，我们必须制作以pb为模的pk同余数表。限于篇幅问题，我们只显示以内的以pb为模的pk同余数表（表1）。该表交叉点的数据显示的是pk≡r mod pb中余数r的数值。比如：附表1中横7和竖149交叉点的数据2显示的是149≡2mod 7中的余数2。

表1 以pb为模的pk同余数表（pk≤168，pb≤

表1 以pb为模的pk同余数表（pk≤168，pb≤

?

2 采用数学归纳法证明命题2

2.1 取初始值验证命题2成立。

由于当2a＝6和2a＝8时，模pb不存在或者pb＝2，谈不上解的问题，所以从2a＝10开始验证。

当2a＝10时，

查以pb为模的pk同余数表，得出此时的数表为表2。

表2 以pb为模的pk同余数表（pk≤10，pb≤

表2 以pb为模的pk同余数表（pk≤10，pb≤

pk pb

表2显示的同余关系为：

比较式（4）和式（5），显示x1有3个可能值。在这3个可能值选任何一个，都会漏掉另外2个pk。按照“不重不漏”的原则，选谁都不合适。可见由该表得出式（4）中的x1无解。即命题2成立。

同理可证当2a＝12、2a＝14…2a＝24时命题2成立。

当2a＝26时，由式（2）得：

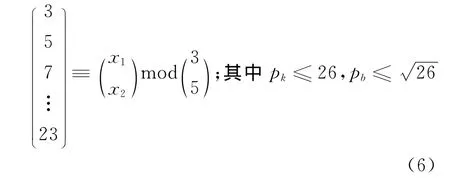
查以pb为模的pk同余数表，得出此时的数表为表3。

表3 以pb为模的pk同余数表（pk≤26，pb≤

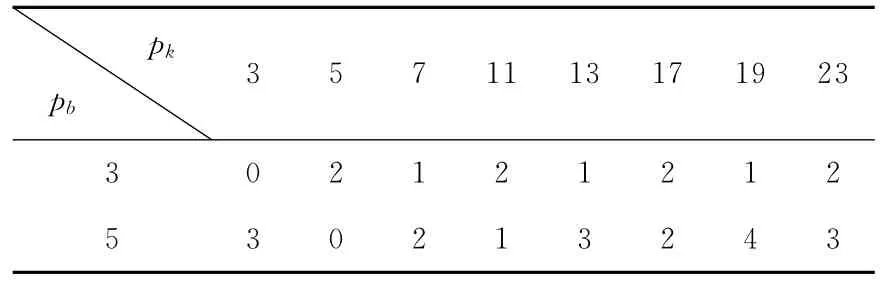
表3 以pb为模的pk同余数表（pk≤26，pb≤

?

表3显示的同余关系为：

比较式（6）和式（7），经过4×6＝24种（模3有4种可能，即0、1、2和不出现；模5有6种可能，即0、1、2、3、4和不出现）可能性筛选计算，不能够找到（6）中的x1，x2，将 ｛3 5 7 …23｝ 这8个元素不重不漏的同模同余表示完毕，也就是说，由该表得出（6）中的x1，x2无解。即命题2成立。

同理可证当2a＝28、2a＝30…2a＝48时命题2成立。

2.2 数学归纳法最关键的递推

假设当2a＝2n（n≥5，且n∈N）时命题2成立，递推证明当2a＝2（n＋1）时命题2也成立。

2.2.1 假设部分

由于当2a＝2n（n≥5，且n∈N）时命题2成立，故下列同余式方程组无解。

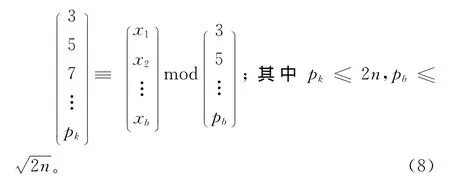
查以pb为模的pk同余数表，得出此时2a＝2n的数表为表4。

表4 以pb为模的pk同余数表（pk≤2n，pb≤

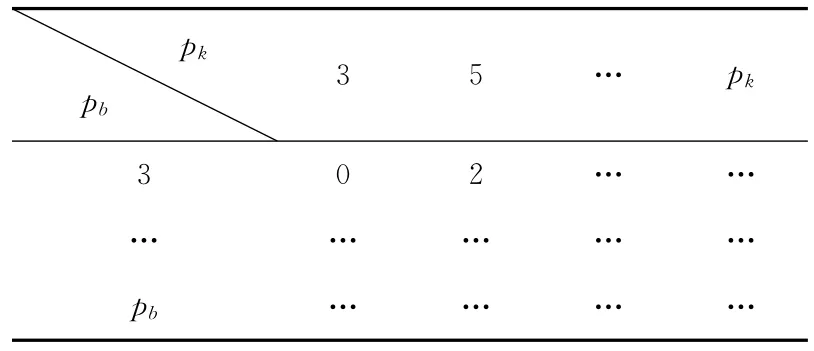
表4 以pb为模的pk同余数表（pk≤2n，pb≤

pb 3 5…p pk k… ………………pb …………

由该表能够得出式（8）中的x1，x2，……xb无解，即命题2成立。

2.2.2 递推部分

（1）第1种情况

第1种情况：2a从2n到2（n＋1）没有引起pk和pb的变化。此时，2a＝2（n＋1）所对应的数表与2a＝2n所对应的数表（表4）相同。由表4可以得知：x1，x2，……xb无解，故此种情况下，命题2成立。

（2）第2种情况

第2种情况：2a从2n到2（n＋1）没有引起pb的变化，但是pk发生了变化。此时，2a＝2（n＋1）所对应的数表与2a＝2n所对应的数表（表4）行数相同，列数增加了一列。（表4）原本无解，列数增加进一步导致数表所对应的x1，x2，……xb更加无解，故此种情况下，命题2成立。

（3）第3种情况

第3种情况：2a从2n到2（n＋1）没有引起pk的变化，但是pb发生了变化。此时，2a＝2（n＋1）所对应的数表与2a＝2n所对应的数表（表4）列数相同，行数增加了一行。这说明，2n＋1＝。即2n＝－1，2（n＋1）＝＋1。

关于这种情况，我曾经给出模量空间放大法和反证法2种证明方法[1－2]。这里再给出与上述模量空间放大法和反证法相互佐证的模量空间数表放大法和数表反证法。

模量空间数表放大法的基本思想在模量空间｛3，5，7，…pb｝下式（2）无解，那么我们可以放大模量空间到 ｛3，5，7，…pb＋1｝下，式（2）仍然无解。

模量空间数表放大法的证明步骤：

第1步，假设：在模量空间 ｛3，5，7，…pb｝，式（2）无解，但是放大模量空间增添一个紧邻的奇素数pb＋1时，式（2）有解。

第2步，递推：因为式（3）减去式（2）的相对应方程式就会得出式（1），所以式（3）和式（2）中x1，x2，…xb是相同的。在pb＋1出现时，由式（3）就会得出一组x1，x2，…xb＋1。这时选取2a＝－1作为参照数，把2a＝－1代入式（3）就可以得出式（9）：

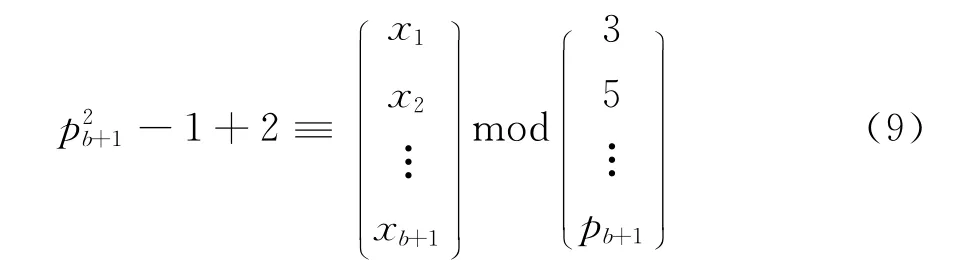
由式（9）进一步可以得出式（10）：

式（10）中mi是用来保证余数小于模数的正整数。

第3步，依据假设继续递推：因为假设“放大模量空间增添一个紧邻的奇素数pb＋1时，式（2）有解”，所以把式（10）代入式（2）得出式（11）：

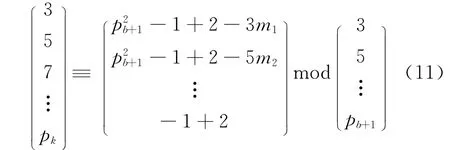
式（11）中mi是用来保证余数小于模数的正整数。

这意味着在 ｛3，5，7，…pb｝的条件下，式（2）中没有筛掉的素数p遗漏有下列同余式成立：

即p遗漏＝2kpb＋1＋1，其中k为任意使得p遗漏为小于－1的素数的自然数。

第4步，揭示矛盾点：

又pb＋1－2k≡0mod p某b，p某b∈Pb

第5步，结论：上述推论与第1步，假设，相矛盾。故数表所对应的x1，x2，……xb＋1仍然无解，于是此种情况下，命题2仍然成立。

数表反证法的假设在这第3种情况下，pb＋1的出现使得式（2）有解。即当2n＝－1时，式（2）无

数表反证法的证明步骤：

第1步，因为式（3）减去式（2）的相对应方程式就会得出式（1），所以式（3）和式（2）中x1，x2，…xb是相同的。在pb＋1出现时，由式（3）就会得出一组x1，x2，…xb＋1。把这时选取2a＝＋1作为参照数，2a＝＋1代入式（3）就可以得出式（12）：

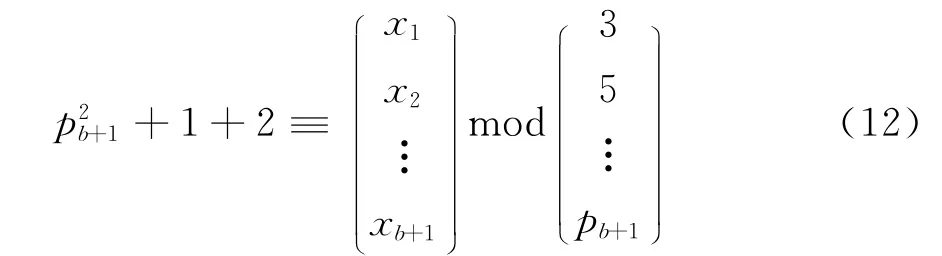
由式（12）进一步可以得出式（13）：

式（13）中mi是用来保证余数小于模数的正整数。

第2步，如果“数表反证法的假设”条件成立—— 在第3种情况下，pb＋1的出现使得式（2）有解，那么，同时可以把式（13）代入式（2）得出式（14）：

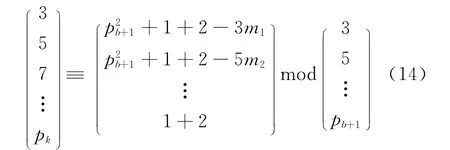
式（14）中mi是用来保证余数小于模数的正整数。

这意味着在条件 ｛3，5，7，…pb｝下或者在2n＝－1时，式（2）中没有筛掉的素数有下列同余式成立：

即p遗漏＝2kpb＋1＋3，其中k为任意使得p遗漏为小于＋1的素数的自然数。

第3步，揭示矛盾点。

又pb＋1－2k≡0mod p某b，p某b∈Pb

关于第3种情况这种证明方法的2点说明：

首先，命题1和命题2的模域空间可能不一致，这将导致模量空间数表放大法和数表反证法的推导不完备。即命题2的模域空间为 ｛3，5，7，…pb｝，而命题 1 的 模 域 空 间 为 ｛p01，p02，p03，…p0k｝ ⊂｛3，5，7，…pb｝时，模量空间数表放大法和数表反证法的推导不完备。但是，由于所推出的结论是“无解”，而导致命题1和命题2最可能有解的模域空间是 ｛3，5，7，…pb｝，所以命题1和命题2的模域空间我们 可 以 认 为 是 ｛3，5，7，…pb｝。理 由 是 在 模 域｛3，5，7，…pb｝上 尚 “无 解 ”， 则 模 域 为｛3，5，7，…pb｝的真子集时更加“无解”。

（4）第4种情况

第4种情况：2a从2n到2（n＋1）引起了pk和pb的共同变化，这种情况是不会存在的。原因很简单，那就是：如果2a从2n到2（n＋1）“pk增加了一个的同时，pb也增加了一个”，这就意味着pk＋1＝—— 这是矛盾的。即第4种情况不存在。

2.3 证明结论

综合2.1和2.2，根据数学归纳法得出：命题2恒成立。即，任意2a（a≥5）以内的所有奇素数，不可能以内的奇素数为模进行同模同余表示。

由于原命题、命题0、命题1、命题2的等价关系，所以哥德巴赫猜想成立。

[1]叶雉鸠.哥德巴赫猜想的证明[J].科技信息，2011（25）：206－207.

[2]叶雉鸠.“哥德巴赫猜想的证明”的几点说明[J].科技信息，2011（33）：460－469.