统计学中参数假设检验拒绝域的确定

杨 刚

（陕西理工学院数学与计算机科学学院，陕西 汉中723000）

0 引言

同数理统计教材相比，一般统计学教材中假设检验的方法和步骤常常显得十分简洁、直观，但这样做的缺点也很明显：一些数学推理过程被屏蔽起来，解题过程十分抽象、步骤间跨度较大，推理不清晰。这样的教材对非统计学专业和非数学专业的教师、学生而言无疑大大加重了他们讲解、学习这门课程的难度，使他们感到假设检验的过程十分抽象，令人困惑。因此在教学过程中，把这些被许多统计学教材没有涉及到的推理内容搞清楚是十分必要的。

1 假设检验的基本思想

1.1 假设检验采用的逻辑推理方法是反证法

为了检验某假设是否成立，先假定它正确，然后根据样本信息，观察由此假设而导致的结果是否合理，从而判断是否接受原假设。

假设检验使用了一种类似于“反证法”的推理方法，它的特点是[1]：

（1）先假设总体某项假设成立，计算其会导致什么结果产生。若导致不合理现象产生，则拒绝原先的假设。若并不导致不合理的现象产生，则不能拒绝原先假设，从而“接受”原先假设。

（2）它又不同于一般的反证法。所谓不合理现象产生，并非指形式逻辑上的绝对矛盾，而是基于小概率原理。

1.2 进行假设检验的基本原理是小概率原理[2]

小概率原理是指发生概率很小的随机事件在一次实验或个别实验中是几乎不可能发生的。如果在原假设成立的前提下发生了小概率事件，则认为原假设是不合理的；反之，如果小概率事件没有发生，则没有证据拒绝原假设。

假设检验是基于样本资料来推断总体特征的，而这种推断是在一定概率置信度下进行的，而非严格的逻辑证明。因此，置信度大小的不同，有可能做出不同的判断。

2 双侧检验拒绝域的确定

在双侧检验问题中，一般统计学教材中的解题步骤简洁、清晰，但推理过程含混、抽象，甚至一些推理略而不提。不妨以一个总体的总体均值和正态总体方差的假设检验为例。

2.1 总体均值的双侧假设检验

例1：某机床厂加工一种零件，根据经验知道，该厂加工零件的椭圆度近似服从正态分布，其总体均值为μ0＝0.081mm。今换一种新机床进行加工，抽取n＝200个零件进行检验，得到的椭圆度均值为0.076mm，样本标准差为s＝0.025mm。问新机床加工零件的椭圆度的均值与以前有无显著差异[2]？（α＝0.05）。

许多统计学教材中对此题的求解过程如下：解：H0：μ＝0.081，认为新旧机床加工零件的椭圆度的均值没有显著差异；

H1：μ≠0.081，认为新旧机床加工零件的椭圆度的均值有显著差异；

由题意可知这是一个双侧检验问题，拒绝域应该在抽样分布曲线的左、右尾部，如图1所示。

由题意可知，μ0＝0.081mm，s＝0.025mm，＝0.076mm，n＝200。由于大样本，故可以用z统计量。

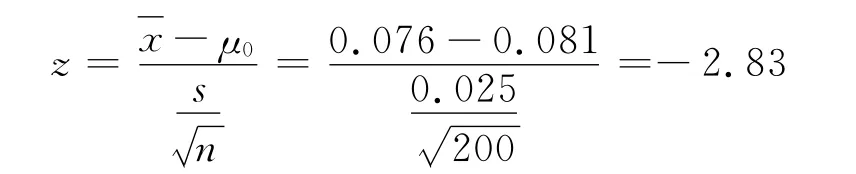
在显著性水平α＝0.05下，拒绝H0，认为新旧机床加工零件的椭圆度的均值有显著差异。

图1 双侧检验示意图

在上述解法中，为什么本题是双侧检验而不是左单侧检验或右单侧检验，因其讲述不清，没有令人可信的数学推理过程，因此很有必要把上面解题过程中为什么采用双侧检验的原因搞清楚。

由于要检验的假设涉及总体均值，故可借助于样本均值来判断。因为是μ的无偏估计量。所以，若H0为真，则不应太大，又1），故衡量的大小可归结为衡量的大小[3]。于是可以选定一个适当的正数k，当观察值满足时，拒绝假设H0。反之，当观察值满足时，接受假设H0。因为当H0为真时），由标准正态分布分位数的定义：

令k＝zα／2，当时，拒绝 H0；当时，不拒绝H0。

这就是一般统计学教材中进行双侧假设检验时没有涉及到的内容（甚至一些数理统计教材中也没有涉及到）。

2.2 正态总体方差的双侧假设检验

设总体 X ～ N（μ，σ2），其中μ、σ2均未知，X1，X2，…，Xn为来自总体X的样本（样本容量为n），由样本可以计算出样本方差为s2。（已知显著性水平为α）

如果遇到如下的双侧检验问题：H0：σ2＝，H1：σ2≠，其中σ0为已知常数。

由于s2是σ2的无偏估计，则当H0为真时，比值在1的附近摆动，此值不应该过分大于1或者过分小于1。由抽样分布的相关定理可知：

当H0为真时取作为统计量则拒绝域的形式为：

P（当 H0为 真， 拒 绝为了计算方便，习惯上取由χ2分位数的定义得：

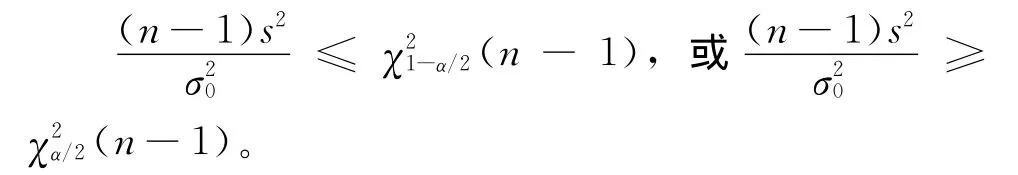
又因为n＝26，α＝0.02，由题意可用χ2检验。查表 可 得（n － 1）＝（25）＝ 44.314，（n－1）＝（25）＝11.524，故拒绝域为：

在上述推理的基础上，关于正态总体方差的双侧检验问题常常在统计学教材中就可以按照下列例2所示的简洁过程进行假设检验。这也是统计学教材中强调统计方法的具体应用，淡化推理推导的思想的具体体现。

例2：某厂生产的某种型号的电池，其寿命长期以来服从方差σ2＝5 000（h2）的正态分布，现有一批这种电池，从它的生产情况来看，寿命的波动性有所变化。现随机取26只电池，测出其寿命的样本方差s2＝9 200（h2）。问根据这一数据能否推断这批电池的寿命的波动性较以往的有显著的变化？（α＝0.02）

解：由题意：H0：σ2＝5 000，H1：σ2≠5 000，

3 单侧检验拒绝域的确定

不妨以一个总体的总体均值的右单侧假设检验为例。

例3：某工厂生产的一种电子元件，在正常情况下，其使用寿命X（h）服从正态分布 N（2 500，1202）。某日从该厂生产的一批这种电子元件中随机抽取16个，测得样本均值假定电子元件寿命的方差不变，问能否认为该日生产的这批电子元件的寿命均值不小于2 500（h）？（α＝0.05）

首先分析问题：由题意可以设计原假设和备择假设如下：

H0：μ≥2 500；H1：μ＜2 500，这里μ0＝2 500，σ0＝120。又由抽样分布的相关定理可选z＝作为统计量。又因为是μ的无偏估计，当H0成立时大一些较为合理，它较小就不合理了，因此较小是小概率事件。如果记P（z＜b）＝α，但是，由于μ≥μ0。因此，μ0不是正态总体的均值，从而z的分布未知，在此我们无法求得b值。为此，再另选一个统计量它服从标准正态分布。当H0成立时，有z＊≤z，于是有：P（z＜b）≤P（z＊＜b），这表明事件（z＜b）是比事件（z＊＜b）发生的概率还要小的小概率事件[4]。因此，只要令P（z＊＜b）＝α，由于z＊服从标准正态分布，查表得b＝－zα，从而有：P（z＜－zα）≤α，于是H0的拒绝域为：z＜－zα。

在上述推理的基础上，许多统计学教材上的解法如下：

解：H0：μ≥2 500，认为该日生产的这批电子元件的寿命均值不显著小于2 500（h）；

H1：μ＜2 500，认为该日生产的这批电子元件的寿命均值显著小于2 500（h）；

又因为：μ0＝2 500，σ0＝120，n＝16，故可以采用z统计量

又因为显著性水平α＝0.05，查表得zd＝z0.05＝1.645，此 时－2.17，故z＜－zα，于是拒绝H0，接受H1。即认为该日生产的这批电子元件的寿命均值μ显著小于2 500（h）。

对于一个总体参数的其他假设检验问题可以按照类似的方法进行推理，此处不再赘述。

4 结语

假设检验是推断统计的重要内容之一，对它进行深入的理解和掌握是十分重要的。但由于现行的许多统计学教材变重应用而轻推理的思想的影响，导致假设检验求解过程被简化、淡化。殊不知这从另一方面反而加重了教师、学生学习统计学的难度，在某些院校一定程度上造成了这门课程教师不愿教或教不透，学生不愿学或学不懂的局面，建议在统计学教材中应该适当补充一些基本的推理、推导过程，这样才能使这门课程显得比较通俗易懂。

[1]MBA智库百科.假设检验[OL].厦门：MBA智库百科，2008[2012－04－26].http：／／wiki.mbalib.com／wiki／假设检验.html.

[2]贾俊平，何晓群，金勇进.统计学[M].4版.北京：中国人民大学出版社，2009：212－214.

[3]教学资源库.辽宁石油化工大学－概率论与数理统计教案08[OL].上海：教学资源库，2008[2012－04－26].http：／／down.math.org.cn／dispbbs.asp？boardid＝40＆Id＝3504.

[4]李晓红.假设检验中原假设的选取问题[J].平原大学学报，2006，23（6）：122－124.