多进制LDPC编码调制系统在衰落信道下的性能分析＊

吕 娟 陈少昌 陈希球 杨雪飞

（1.长江工程职业技术学院 武汉 430212）（2.海军工程大学 武汉 430033）（3.海军装备研究院 北京 100073）

1 引言

多进制低密度奇偶校验（Low-Density Parity-Check，LDPC）码及其迭代译码算法 QSPA（Q-ary Sum-Product Algorithm）由Davey和 Mackay于1998年首次提出［1］，相比于二进制LDPC码，其具有更好的差错性能优势［2］。现代通信系统越来越需要可靠且频谱有效的传输，多进制LDPC编译码技术可保证传输的可靠性，而频谱有效性可通过高阶调制来获取。研究多进制LDPC码的编码调制系统主要有两个方向：一个是多级编码调制（MultiLevel Coding，MLC）［3］；另 一 个 是 比 特 交 织 码 调 制 （Bit Interleaved Coded Modulation，BICM）［4～5］。这两种系统都是基于高阶调制的，两者的区别在于BICM只需要一个编译码器，而MLC需要采用多个编译码器。为了减少系统的复杂度，本文主要仅考虑多进制LDPC-BICM的编码调制系统。多进制LDPC-BICM系统可以获得更好的纠错性能，码字自身的内在交织性可完成各信息符号之间的交织，能达到更高的数据传输速率和频谱效率。

传输信道的特征在很大程度上决定了通信系统的性能，在数字通信理论中最经常使用的是加性高斯白噪声（Additive White Gaussion Noise，AWGN）信道，然而在实际应用的很多情况下AWGN信道不能满足描述信道特征的要求而必须采用非高斯信道模型，无线移动信道就是实际移动通信环境的一种，多径衰落是其主要的特点。目前对于多进制LDPC-BICM的研究大多集中在AWGN信道上［6～7］，对Rayleigh信道和 Rice信道研究的文章相对较少［8～10］。本文将首先介绍Rayleigh和Rice信道的仿真模型，在此基础上建立了多进制LDPC-BICM系统，分析了在衰落信道下迭代译码的初始化条件，最后给出了仿真结果和分析。

2 衰落信道

多径接收信号的幅度包络变化一般服从Rayleigh分布和Rice分布［11］。在移动无线信道中，Rayleigh衰落分布是常见的用于描述平坦衰落信号或独立多径分量接收中包络的时变统计特性的一种衰落类型；Rice衰落分布是由于在瑞利衰落分布的基础上，存在一条直射路径的影响而造成的。

Rayleigh衰落信道中不存在一个较强视距直射路径，当多径信道的信号幅度包络服从Rayleigh分布，其相应的概率密度函数为

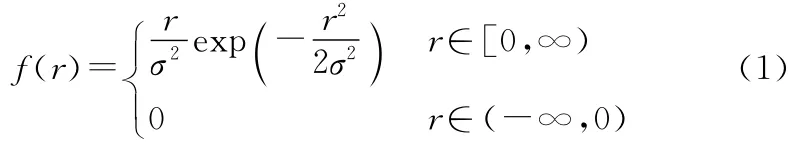
Rice衰落信道是视为在Rayleigh衰落多径上叠加了一个主要的静态信号分量，该路径信号的强度往往比其它路径大得多，其相应的概率密度函数为

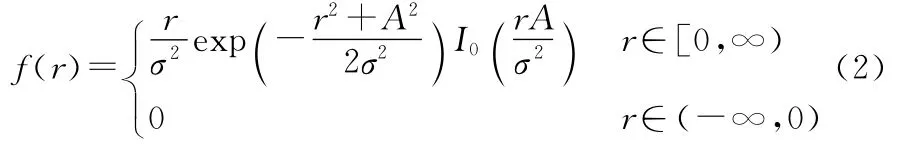
其中，参数A为直射波幅度的最高峰值，I0（x）为第一类零阶修正Bessel函数。莱斯因子K为直射波信号与多径散射分量信号能量之比，其能够完全确定Rice分布。当直射信号幅度趋于零时，Rice分布就变为Rayleigh分布，可见，Rayleigh分布是Rice分布的特例。图1和图2分别给出了服从Rayleigh和Rice分布的信号衰落幅度包络和频度分布情况，其中Rice分布中莱斯因子K＝5dB。

图1 Rayleigh衰落包络及概率密度分布

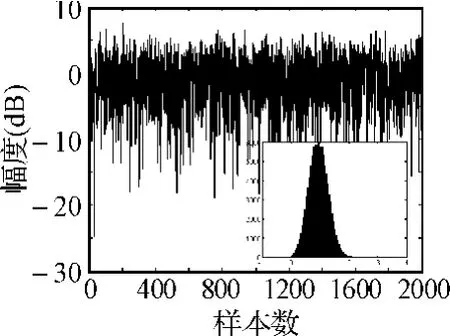
图2 Rice衰落包络及概率密度分布

3 系统模型

传统的编码调制系统在编译码与调制解调之间需要交织与解交织器，由于LDPC码校验矩阵中非零值的随机分布特性及其高度稀疏性，使LDPC码本身具有内在交织性。在多进制LDPC码编码的同时，也完成了各信息符号之间的交织，因此，构造多进制LDPC码编码调制系统时，可省略交织与解交织器，从而降低系统的复杂度并缩短了时延。多进制LDPC码的编码调制系统如图3所示。采用q进制LDPC码与M阶调制结合（M＝q）的编码调制方式，可以提供更高的数据传输速率和频谱效率，有利于带宽有效传输；同时可以避免发送端和接收端比特与符号之间软信息转换。

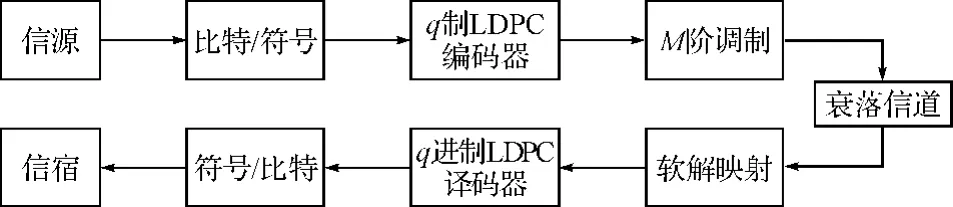
图3 多进制LDPC编码调制系统框图

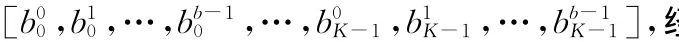
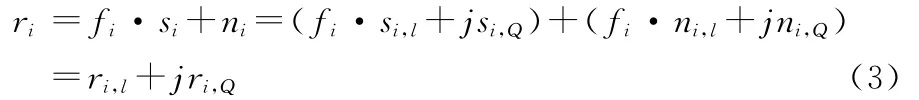
其中，ni，l、ni，Q为两个独立同分布均值为零方差为σ2的高斯白噪声。

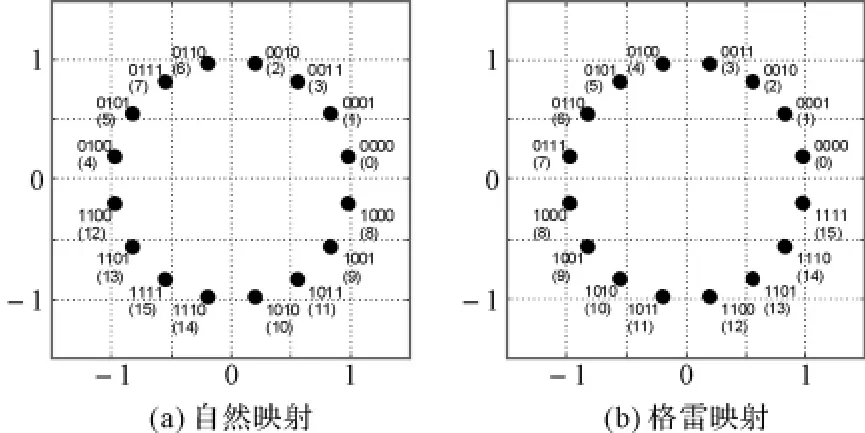
图4 不同映射方式的16PSK星座图

接收向量ri，l、ri，Q的联合概率密度为

假设发送各符号的先验概率相等，则后验概率为

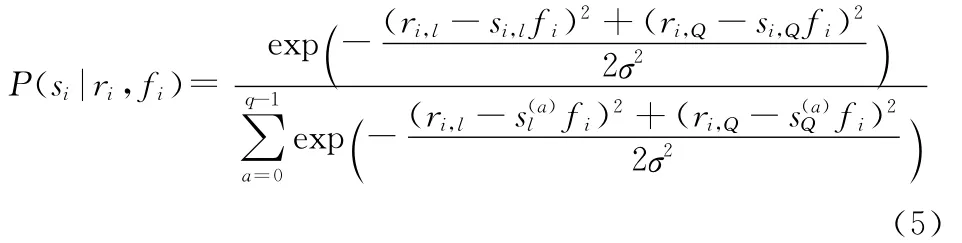
4 仿真实验及性能分析

本节对多进制LDPC编码调制系统在Rayleigh和Rice信道下进行了性能仿真和比较分析。多进制LDPC码选用结构化的多进制QC LDPC码，仿真的迭代译码算法采用FFT-QSPA算法，二进制LDPC码译码采用和积算法（Sum-Product Algorithm，SPA）。最大的迭代次数都设置为50。

首先将多进制LDPC-BICM系统与二进制LDPC-BICM系统进行对比说明多进制LDPC码与高阶调制结合的优势。选用有限域第I类构造方法构造出同比特长度同码率的多进制和二进制LDPC码。16-ary（225，173）LDPC码是基于GF（24）域的有限域第I类构造方法［12］，该多进制码的校验矩阵H是一个由具有15×15循环置换矩阵的4×15阵列构成的大小为60×225矩阵，其列重行重分别为4和14。二进制（899，691）LDPC码采用基于GF（25）域的有限域第I类构造方法［13］，该二进制码的校验矩阵H是一个由具有31×31循环置换矩阵的13×29阵列构成的大小为403×899矩阵，其列重行重分别为13和28。16进制LDPC编码调制和二进制LDPC编码调制在AWGN信道下的性能仿真如图5所示。在FER为10－4处，多进制LDPC编码调制较二进制LDPC编码调制取得了大约10.28dB的编码增益，体现出了多进制LDPC码与高阶调制结合的优势。

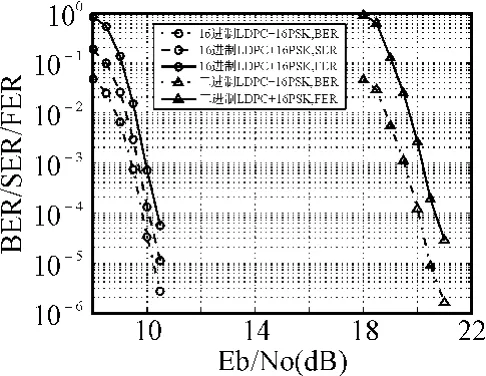
图5 多进制和二进制LDPC编码调制系统的误码性能比较

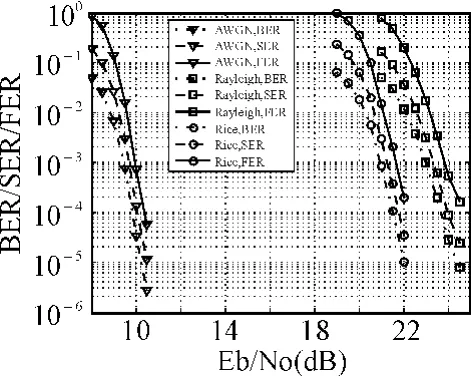
图6 16进制（225，173）QC LDPC编码高阶调制系统的误码性能

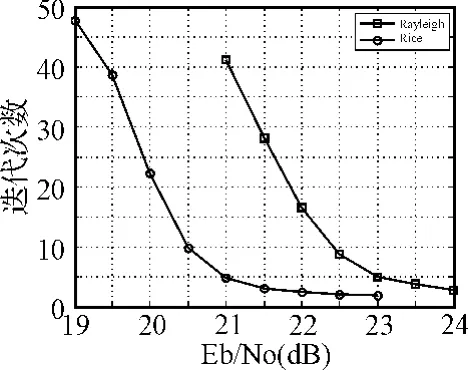
图7 16进制（225，173）QC LDPC编码高阶调制系统的平均迭代次数

图6给出了16-ary（225，173）LDPC码采用格雷映射16PSK调制方式在AWGN、Rayleigh和Rice信道下的误码率曲线图，其中莱斯因子K＝5dB。图7给出了对应的平均迭代次数曲线图。从图6和图7可以看出，在Rayleigh和Rice信道下，多进制LDPC编码高阶调制系统均表现出良好的误码性能，在高信噪比下也未出现误码平台，迭代译码在较小的迭代次数下就能达到收敛。

5 结语

在多进制码型当中，目前应用最为广泛的是RS码，其在衰落信道下具有很好的误码性能。与RS码相比，多进制LDPC码不仅具有多进制码型的抗突发特性，而且还采用了软判决迭代译码算法，使得误码性能更为优越。本文建立了多进制LDPC编码调制系统，给出了Rayleigh和Rice衰落信道下多进制LDPC码迭代译码的初始化条件，讨论了多进制LDPC码在衰落信道下的性能。研究结果表明，LDPC码具有良好的抵御衰落干扰的特性。

［1］Davey M C，Mackay D.Low-density parity check codes over GF（q）［J］.IEEE Commun.Lett.，1998，2（6）：165-167.

［2］李丹，白宝明，孙蓉.多元LDPC码与二元LDPC码的性能比较［J］.无线通信技术，2007（3）：1-6.

［3］Arabaci M，Djordjevic I B，Saunders R，et al.Nonbinary quasi-cyclic LDPC-based coded modulation for beyond 100trans-mission［J］.IEEE Photon.Technol.Lett.，2010，22（6）：434-436.

［4］Zhao D，Ma X，Chen C，et al.A low complexity decoding algorithm for majority-logic decodable nonbinary LDPC codes［J］.IEEE Commun.Lett.，2010，14（44）：1062-1064.

［5］Baldi M，Chiaraluce F，Cancellieri G.Finite-precision analysis of demappers and decoders for LDPC-coded M-QAM systems［J］.IEEE Trans.Broadcasting，2009，55（2）：239-250.

［6］王哲，栾英姿.基于Q矩阵的LDPC码编码设计方法［J］.计算机技术与发展，2010，20（6）：201-204.

［7］刘晓明，彭芳芳，吴皓威，等.基于IEEE802.16e的LDPC编译码方案设计与实现［J］.2009，19（5）：205-208.

［8］孙韶辉，贺玉成，王新梅.低密度校验码在瑞利衰落信道中的性能分析［J］.计算机学报，2002，25（10）：1077-1082.

［9］林家儒，吴伟陵.LDPC码在RICE信道中的性能分析［J］.北京邮电大学学报，2004，27（2）：48-53.

［10］林家儒，吴伟陵.非规则LDPC码在RICE信道中的性能分析［J］.电子学报，2005，33（1）：43-46.

［11］Kostov N.Mobile radio channels modeling in MATLAB［J］.Radio Engineering，2003，12（4）：12-16.

［12］Zeng L，Lan L，Tai Y Y，et al.Constructions of nonbinary quasi-cyclic LDPC codes：A finite field approach［J］.IEEE Trans.Commun.，2008，56（4）：545-554.

［13］Lan L，Zeng L，Tai Y Y，et al.Constructions of quasi-cyclic LDPC codes for AWGN and binary erasure channels：A finite field approach［J］.IEEE Trans.Inf.Theory，2007，53（7）：2429-2458.