基于PIC-MCC的纳米放电加工放电通道模拟及其机理研究

陈 寅,赵万生

(上海交通大学机械与动力工程学院,上海 200240)

电火花加工是一种非接触加工方法,具有不受工件材料强度、硬度等机械性能限制及宏观加工力小等优点,在常规加工和微细加工领域都占有重要位置。电火花加工可方便地通过控制微小放电能量来获得最小的加工去除单位,理论上可实现单层原子级的材料去除,具备纳米尺度加工的潜能,还具有加工成本低的优点,从而使低成本、高集成度的微纳尺度器件、传感器及微纳仪器关键部位的加工甚至产业化成为可能。

国外学者已对纳米电加工的可能性、工艺及机理进行了初步探索。国枝正典等通过在电路中采用耦合电容的方法进行双极性放电加工,抵消了回路中杂散电容的负面影响,加工出直径小于500 nm的电蚀坑[1]。Rajurkar等用钨探针在原子力显微镜上分别对置于空气、去离子水和油等不同介质中的金和铜涂层进行电加工,观察到了一系列现象,如在空气中探针经过工件表面会引起金原子堆积,而在去离子水和油中则引起材料去除;此外还研究了AFM扫描力对涂层表面的影响[2]。Virwani和Malshe等以STM 为加工平台、绝缘油(正葵烷)为工作介质,使用尖端半径为35 nm的铂铱合金或钨探针为工具电极在金表面加工出直径约为10 nm的小坑[3-5]。目前纳米电加工的机理还未获得很好的解释,但Rajurkar和Malshe均认为其纳米尺度材料去除的机理应该是以放电加工为主,而没有微机械加工或电化学加工的证据。这为放电加工方法实现纳米加工提供了有力的支持。

国内对微纳米尺度放电加工的研究主要集中在以微米尺度加工特征为对象的微细放电加工方面。崔景芝建立了气中放电通道模型,采用粒子模拟方法对电火花等离子放电通道的形成过程和振荡特性进行模拟研究,分析了微细放电通道形成和振荡的机理[6]。王振龙等研究了空气中的放电沉积现象,证实纳米尺度放电加工不仅具有去除能力,还具有沉积能力[7]。赵万生等对微细电火花加工进行了多方面的研究,并尝试采用单次脉冲放电法加工出尖端半径100 nm的钨电极[8]。

本文以纳米尺度放电加工为对象,采用粒子模拟方法,结合蒙特卡罗碰撞模型和二次电子发射模型,对纳米尺度等离子体放电通道击穿过程的粒子运动、电磁场变化等进行仿真模拟,尝试用相关物理知识对纳米尺度放电加工过程进行合理的描述和解释。对比纳米尺度与传统微细尺度放电通道击穿过程的异同,探索纳米尺度下放电加工的新机理,并对纳米尺度的加工特征进行理论预测。

1 放电通道模拟相关的理论与算法

1.1 放电通道形成机理

汤森理论表明,在极间电场足够大时,电子在电场中获得足够能量使气体粒子产生激发和电离,新生的电子和离子在电场作用下又获得能量产生激发和电离,以致电子向阳极运动过程中带电粒子浓度按指数规律增长,形成雪崩式电离。在电火花加工中,随着极间电压升高和极间距离减小,当阴极表面某处场强达到105V/mm左右时,场致电子将由阴极表面向阳极方向逸出。在电场力作用下,高速运动的电子撞击介质中的分子或中性原子,发生碰撞电离,进而形成大量带电粒子,即发生雪崩式电离,使介质击穿形成放电通道。此时由于通道扩张压力大于自洽磁场约束力与介质阻力之和,等离子体将沿通道径向向外运动,放电通道迅速扩张。随着通道扩张压力迅速下降,当其与自洽磁场约束力及介质阻力之和相等时,径向扩张停止,放电通道处于平衡状态[9]。

1.2 PIC-MCC模型

粒子模拟法(Particle In Cell,PIC)通过模拟计算跟踪大量单个微观粒子的运动,对其进行统计平均,由此得到宏观物质特性及其运动规律。因其能跟踪大量粒子并动态模拟各种物理量的变化,尤其是极短时间内的暂态过程,故能实现具体实验中一些难以观察的过程和现象(如ns级过程)。PIC法已成为等离子体模拟研究的一种重要工具。

蒙特卡罗碰撞(MCC)模型从碰撞次数的概率分布出发,基于随机数计算得到平均碰撞次数,以此作为碰撞概率。MCC模型补偿了传统方法中忽略的多次碰撞,可提高计算精度。PIC-MCC模型适用于非平衡状态的低温等离子体参数模拟[10]。

PIC法时间步长受到多种限制[11],如差分方程稳定性条件CFL限制(cΔ t/Δ x＜1)、等离子体频率限制等。引入MCC模型后,还需满足空碰撞模型Vahedi限制,即限制一个时间步长内总碰撞概率小于0.1[12],这样可避免一个时间步长内出现多次碰撞。

PIC-MCC模型基本循环过程见图1。首先,将所要研究的空间区域划分为许多网格,设定带电粒子的初始位置和速度;其次,对它们统计平均求出等离子体空间的电荷和电流密度;然后通过求解Maxwell方程组得到空间网格上的自洽电磁场,推出粒子所处位置的电磁场;最后,求解粒子运动方程,得到新的粒子位置和速度,并采用MCC模型得到碰撞后的位置和速度。这样不断进行迭代求解,从而得到各参量随时间变化的过程。

1.3 二次电子发射模型

当具有一定能量或速度的电子或离子轰击金属、半导体、绝缘体等物体时,会引起电子或离子从这些物体发射出来,这种电子发射的物理现象称为二次电子发射。二次电子发射主要可分为反射型、透射型和轰击传导3类,我们通常所说的二次电子发射是指反射型[9]。目前国内外理论研究认为,气中放电击穿过程主要机理包括碰撞电离、光电离及二次电离。放电间隙较大时,汤森理论能较好地解释放电击穿机理。而微米级或更小的放电间隙不足以发生雪崩式电离,其放电击穿主要是由二次电子发射引起的,而非间隙中气体本身的反应[10]。

国外学者在氩气的电离模拟中习惯使用实验得出的二次电子发射率,即常量8%。Petrovic等[10]认为应考虑二次电子的多种来源,包括金属边界吸收和反射的非流体动力学过程、空间电荷对汤森放电的影响及二次电子的产生与基本放电参数间的线性非线性关系。但目前在模拟中实现困难较大。

2 放电通道模拟结果与分析

为简化模拟,放电空间只采用一种中性气体Ar。采用轴对称圆柱坐标系,故只需计算1/2半径空间。取电子温度4 eV,二次电子发射率8%。采用等离子体PIC模拟软件OOPIC Pro 2.0.2,该软件包含蒙特卡罗模块和二次电子发射模块。电磁模式下时间步长按CFL限制酌情选取,等离子体频率限制和空碰撞模型限制软件自动满足。

2.1 微纳尺度放电通道模拟对比

(1)首先模拟微米级氩气电离。电子束从阴极入射,使极间Ar的中性气体分子发生碰撞电离。模拟参数为:放电间隙 40μm,通道半径 7μm,初始气压0.5MPa,极间电压25 V,时间步长10-13s。

图2是微米级氩气电离放电通道中氩离子和电子的空间分布相图。由模拟结果可观察到明显的放电通道形成过程,击穿时间约为5×10-10s,符合实际加工情况。

(2)初步模拟纳米级氩气电离放电通道。模拟参数为:放电间隙40 nm,通道半径7 nm,初始气压0.5MPa,极间电压25 V,时间步长10-15s。模拟结果见图3。

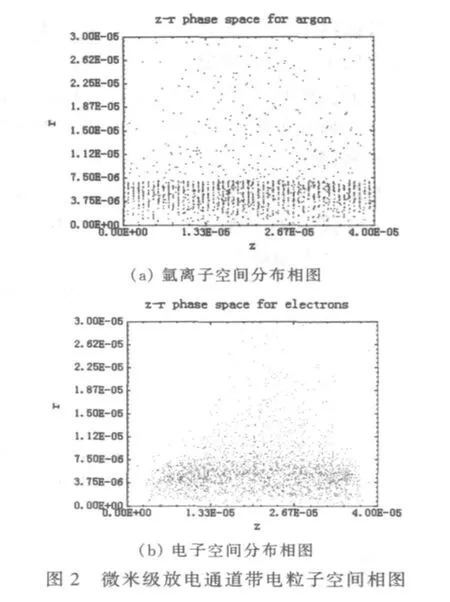
图3a中,锥状区域密度下降,表示中性气体分子被电离,可看到电离区域从阴极至阳极(从左到右)略呈辐射状。与模拟微米级氩气电离结果对比后发现:微米级放电通道形成时,被电离的中性气体分子数目可观,且形成了明显的通道形态,而纳米级通道击穿过程并不明显(这与模型设置过于简化有关)。此外,由动态模拟结果可见,纳米尺度下带电粒子的个体特性变得更显著,运动轨迹具有一定的随机性,这与微米尺度下大量粒子呈现出较规律的波动特性有所不同。这一区别与物质的波粒二象性原理相符合。

2.2 纳米尺度放电通道模型改进

为了对纳米尺度放电通道进行更准确的模拟,力求接近真实实验加工情况,依照目前纳米电加工的典型实验设置[3-5]对模型进行如下改进(图4):以半径35 nm的铂铱合金或钨针尖作为阴极(通道半径取30 nm),表面平整的金试样作为阳极,放电间隙为3 nm,极间电压10 V,初始气压为常压(1 atm),时间步长 10-15s。

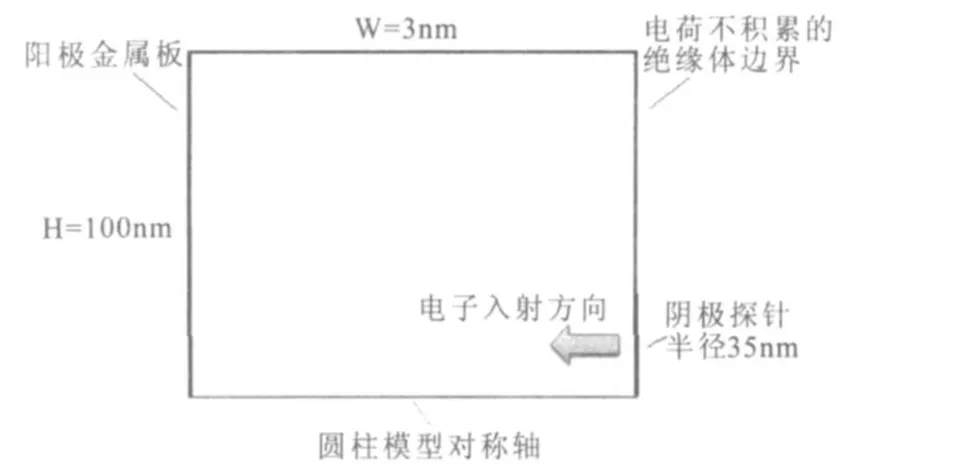
图4 改进后的纳米放电通道示意图

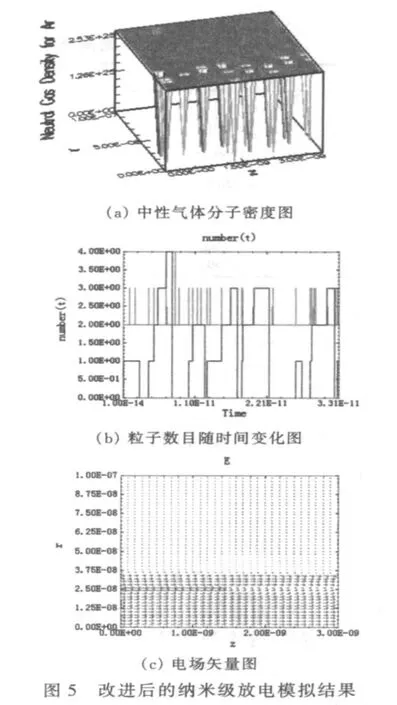
模拟结果显示:1×10-11s左右通道基本形成(图5a),通道内中性气体分子密度下降,说明气体被电离。图5b是离子和电子数目随时间变化图,可看出1×10-11s左右粒子数目达到第一个高峰,即发生击穿。氩离子、电子相图和密度图上结果并不清晰,但在动态模拟结果中已可较清楚地观察到电子持续稳定地从阴极探针尖端向阳极金属板运动,等离子体通道形成。从电场矢量图(图5c)上可较清楚地看出通道形状。放电通道范围内电场强度较大,且具有方向性。

2.3 气体最佳击穿气压存在性验证

由文献[9]可知,要发生稳定的直流放电,需产生足量的电子-离子对以补偿碰撞过程(包括附着、漂移和扩散至边界)中损失的带电粒子。低压情况下电子-中性粒子的碰撞几率很低,因此电离效应不显著;而高压情况下,弹性碰撞使粒子难以获得足够的能量发生电离,且离子-中性粒子的碰撞使离子扩散至边界损失的数量增多。因而在放电间隙确定的情况下,存在气体击穿的最佳气压。用2.2节中改进的纳米级放电通道模型对气体最佳击穿气压的存在性进行验证,同时验证模型的正确性,对实际加工情况进行理论预测。

取气压基准值为P0=10760 Torr(1 Torr=1mmHg)。模拟结果见图6。可见,击穿时间约为7.4×10-12s,此时通道内带电粒子数目首次达到最高峰。

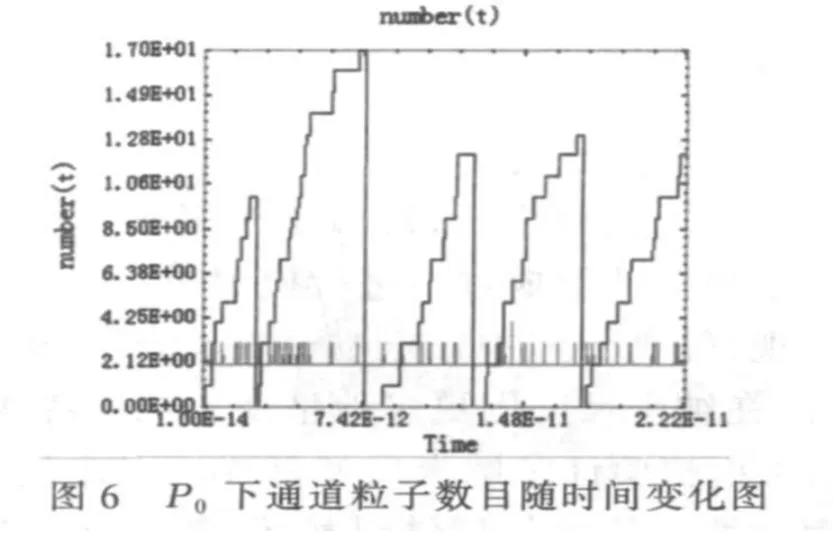
以P0为基准增大和减小气压,模拟气压值及相应的击穿时间数据见表1。可见P=30760 Torr时通道击穿时间延长已较显著,预计继续增加气压,电离效应会越来越弱。这是由于弹性碰撞使带电粒子从边界扩散损失增多,电离发生更困难。同理,P=760 Torr时通道击穿时间已明显延长,预计继续减小气压,电离效应会继续减弱,原因是粒子碰撞几率减小。

由表1数据绘制通道气压-击穿时间关系图,见图7。

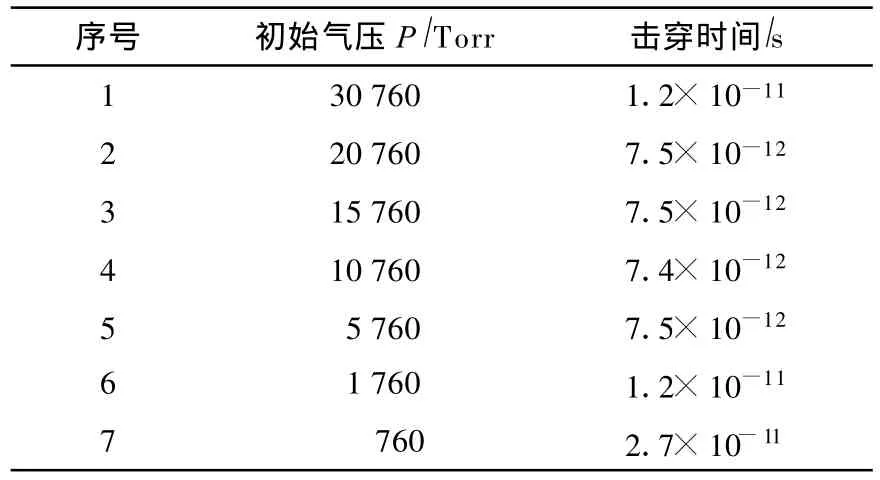
表1 纳米放电通道气压-击穿时间模拟值

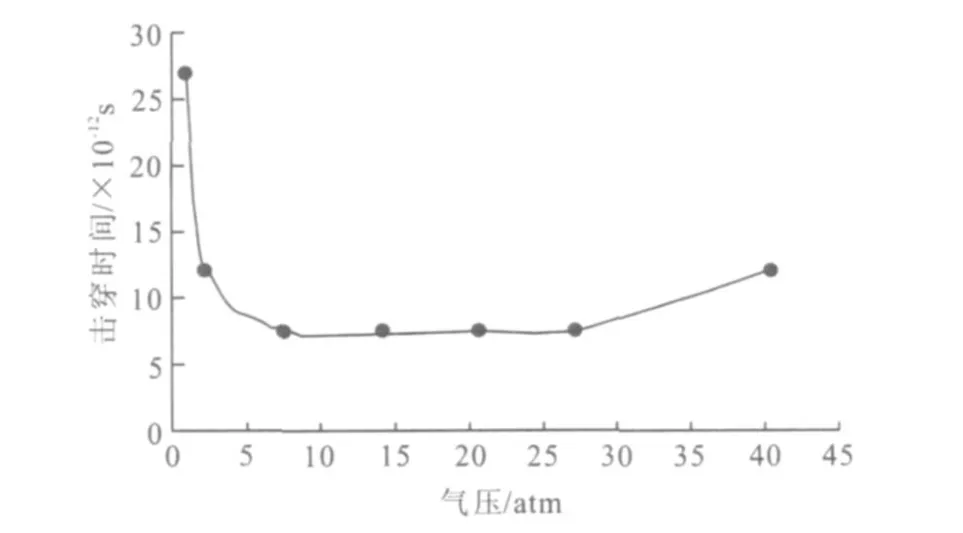
图7 纳米放电通道击穿时间随气压变化图

由图7可见,通道气压在一定范围内(初步认为是5760～20760 Torr/7.6～27.3 atm)的气体电离效果较好,击穿时间约为7.5×10-12s。在此范围外,增加或减小气压都会降低电离效果,使击穿时间延长,验证了气体电离最佳击穿气压的存在性。

3 结论

(1)运用粒子模拟方法,结合蒙特卡罗碰撞模型和二次电子发射模型,对微纳米级氩气电离等离子体放电通道的形成过程进行模拟仿真。通过模拟对比发现,等离子体中带电粒子在微米尺度呈现出波动性,在纳米尺度则更多地呈现出粒子特性。

(2)模拟验证了纳米尺度氩气放电最佳击穿气压的存在性。数据处理结果显示,气压在一定范围内气体电离效果较好,在此范围之外气压偏大或偏小都会降低电离效果,击穿时间会延长。

[1] Kunieda M,Hayasaka A,Yang Xiaodong.Study on nano EDM using capacity coupled pulse generator[J].Annals of the CIRP,2007,56:213-216.

[2] Alkhaleel A H,Yu Zuyuan,Sundaram M M,et al.Nanoscale features by electro-machining using atomic force microscope[J].T ransactions of NAMRI/SME,2006,34:437-444.

[3] Virwani K R,Malshe A P,Rajurkar K P.Understanding dielectric breakdown and related tool wear character-istics in nanoscale electro-machining process[J].Annals of the CIRP,2007,56:217-220.

[4] Virwani K R,Malshe A P,Rajurkar K P.Understanding sub-20 nm breakdown behavior of liquid dielectrics[J].Physical Review Letters,2007,99:017601-1-017601-4.

[5] Kalyanasundaram V,Virwani K R,Spearot D E,et al.Understanding behavior of machining interface and dielectric molecular medium in nanoscale electro-machining[J].CIRP Annals-Manufacturing Technology,2008,57(1):199-202.

[6] 崔景芝.微细电火花加工的基本规律及其仿真研究[D].哈尔滨:哈尔滨工业大学,2008.

[7] Wang Zhenlong,Peng Zilong,Jin Baidong.Technique of micro EDM deposition in air for fabrication of micro spiral structures[C]//Proceedings of the 8th International Conference on Frontiers of Design and Manufacturing.Tianjin,2008:807-810.

[8] Zhao Wansheng,Cao Guohui,Wang Zhenlong,et al.Primary study on instantaneous fabricating mechanism of tungsten microelectrode based on single discharge and its application[J].Key Engineering M aterials,2004,259-260:496-501.

[9] 江剑平,翁甲辉.阴极电子学与气体放电原理[M].北京:国防工业出版社,1980.

[10] Radmilovic-Radjenovic M,Petrovic Z Lj,Radjenovic B.Modelling of breakdown behavior by PIC/MCC code with improved secondary emission models[J].Journal of Physics:Conference Series,2007,71(1):1-19.

[11] Birdsall C K,Langdon A B.Plasma physics via computersimulation[M].New York:Adam Hilger,1991.

[12] Vahedi V,Surendra M A.Monte carlo collision model for the particle in cell method:applications to argon and oxygen discharges[J].Computer Physics Communications,1995,87(1-2):179-198.