基于微分进化神经网络的模拟电路故障诊断✴

赵光权,彭喜元,马勋亮

(哈尔滨工业大学自动化测试与控制系,黑龙江哈尔滨 150001)

模拟电路的故障诊断是当今世界研究的一大热点.模拟电路的故障可分为两大类:一类称为硬故障,指元件的开路和短路失效故障;另一类称为软故障(元件参数故障),指元件的参数超出预定的容差范围,一般它们均未使设备完全失效[1].由于在模拟电路中元件参数具有连续变化的特性,电路的可能状态总数是无穷的,使得采用传统的故障诊断方法对软故障进行诊断相对困难,而基于现代方法的故障诊断方法例如神经网络已逐步受到人们的重视[2-4].

基于神经网络的故障诊断方法不需要建立对象的精确模型,而且其泛化能力与非线性能力使之能够用于解决模拟电路故障诊断中的容差和非线性问题,目前在故障诊断中已得到了广泛的研究和应用.但是,利用经典的BP神经网络进行模拟电路的故障诊断存在如下问题:①网络收敛速度慢,且容易陷入局部最优;②神经网络结构难以确定[5].

针对上述问题,国内外已有不少学者致力于利用进化算法优化神经网络的研究,文献[6]研究了遗传算法训练神经网络的问题,取得了较好的效果,但GA同时存在着易早熟的缺点;文献[7],文献[8]将PSO算法用来训练神经网络的权值.

鉴于微分进化算法(Differential Evolution Algorithm,简称DE算法)独特的思想机制和神经网络的广泛应用,将两者相结合进行研究已成为目前的新方向.本文在分析DE基本算法原理的基础上提出了改进的微分进化算法,并利用改进的DE算法对神经网络进行权值训练.最后,将微分进化神经网络应用到模拟电路故障诊断中,验证算法的有效性和实用价值.

1 改进的DE算法

DE是求解基于连续变量的全局优化算法.假设DE算法种群规模为NP,每个个体有D维变量,则第G代的个体可表示为Xi,G,i=1,2,…,NP.DE算法的主要算子包括:变异、交叉、选择[9].

DE算法和其它进化算法的主要区别是变异方式.变异操作后得到中间个体记为vi,G+1,即

式中:r1,r2,r3∈{1,2,…,NP}为r1≢r2≢r3≢i,F为DE算法中的一个控制参数.

交叉操作如下:将变异得到的中间个体vi,G+1和当前个体Xi,G进行杂交,如式(2)所示.经过杂交后得到当前个体的候选个体.

式中:i=1,…,NP,j=1,…,D.rnbr(i)是一个随机参数保证ui,G+1至少从vi,G+1中取到一个分量值,randb(j)∈[0,1]是一个均匀分布的随机数,杂交因子CR∈[0,1]是DE算法的一个控制参数,它决定了中间个体分量值代替当前个体分量值的概率.

选择操作如下:对候选个体ui,G+1进行适应度评价,然后根据式(3)决定是否选取新产生的个体.

上述操作中,变异机制对DE算法的性能有着很大的影响.标准DE算法有多种变异策略,一般将式(1)所示的变异策略称为基本策略,另一种常用的变异策略如式(4)所示.

式中:Xbest,G表示当前种群中的最优个体.

仔细分析,不难发现:式(1)变异策略的特点是全局性能强但搜索速度慢,式(4)变异策略的特点则是搜索速度快但易陷入局部最优.为此,本文提出了一种混合变异策略的方法,其主要思想是使少部分个体按式(4)进行变异,其余大部分个体仍按式(1)进行变异.其具体方法为:在每个个体变异前,先将当前所有个体的适应度值归一化,然后依据该个体适应度的值在所有个体中所占的位置,以一定的概率选择该个体变异策略是采用式(1)还是式(4).其伪代码如图1所示.

图1中,rand()表示取 0～1之间的随机数,cmin和cmax分别表示上一代个体中的最优个体和最差个体的适应度的值,cost(i)表示要变异的上一代父个体的适应度值,δ是一个常数,根据大量实验,δ一般取0.1.Xr1,G,Xr2,G,Xr3,G是在上一代个体中随机选取的,且Xr1,G≠Xbest,G,r1≠r2≠r3.

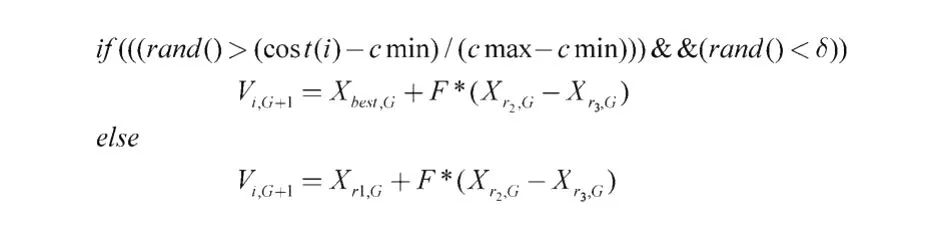
图1 混合变异策略伪代码Fig.1 Pseudocode of hybrid mutation strategy

MDE算法的本质是是每代中的小部分优秀个体以一定概率在当前最优解附近搜寻,并且优秀的个体有相对大的机会在当前最优解附近搜索,而大部分其它个体则仍然进行随机搜索.和基本DE算法相比,MDE算法既使少部分个体以一定的概率增强其贪婪性,又使大部分个体保持其多样性,从而使得MDE能够在保持较强全局多样性的同时加快其收敛速度.

2 基于MDE算法的神经网络训练

在使用神经网络前,首先要通过输入和输出样本集对网络进行训练,亦即对网络的权值进行学习和修正,以使网络实现给定的输入输出映射关系.神经网络的训练过程就是学习的过程,也是确认权值的过程(这里阈值可知,看成系数为 -1的权值,故以后只提权值优化).

BP算法是一种经典的神经网络权值训练算法,同时又有着一定的局限性,主要体现在如下几个方面:①学习收敛速度太慢;②不能保证收敛到全局最小点;③对目标函数的依赖性太强;④没有确定隐层神经元数的有效方法.

鉴于此,本文采用MDE算法来优化神经网络的权值.其基本思想是:首先通过常规办法确定神经网络结构,再将连接权进行编码,然后利用MDE算法在权值空间中搜索最优权值.

2.1 编码方式

本文采用实数编码的方式,每个连接权值用一个实数表示,一个网络的权值用一组实数向量表达,即为DE算法的一个个体.

2.2 适应度函数

在DE算法中,适应度值是群体进化的依据.本文中权值训练适应度函数的选取如式(5)所示.

式中:P表示输入的样本数;M表示神经网络总的层数;y表示神经网络的输出;t表示样本中的实际输出.

在确定了算法的编码方式和适应度函数后,下一步就该用MDE算法对神经网络进行权值优化.优化的过程实际上就是一个算法寻优的过程,每一组权值看成一个个体,个体在寻优过程中不断得到进化,最后得到最优个体,此时神经网络学习完成.

利用MDE算法优化神经网络的步骤如图2所示.

图2 MDE算法优化神经网络Fig.2 Flowchart of neural network trainingwith MDE algorithm

3 模拟电路故障诊断实例

应用神经网络进行模拟电路故障诊断主要有如下几个步骤:

1)产生训练样本集.首先要完成故障状态点选择和测试点的选择,并应用PSPICE软件模拟出电路各测试点的理论值和故障值,并把它建成一个故障状态表.

2)建立神经网络.确定神经网络的种类,并利用训练样本集训练神经网络.本文利用MDE算法来训练神经网络,充分保证其泛化能力.

3)利用训练好了的神经网络进行故障诊断.神经网络训练后,电路的故障字典就建立在神经网络之中,网络的输入节点由电路的可测节点决定,输出节点由故障状态的数目决定.诊断时,将待诊断的故障特征数据输入到神经网络之中,经过计算,神经网络的输出就是故障的类别.

本文以sallen-key滤波电路为例来介绍基于微分进化神经网络的故障诊断方法.sallen-key滤波电路如图3所示[10].

根据灵敏度分析,sallen-key电路中R2和R3,C1和C2的参数变化对电路输出的影响较大,选择这4个器件作为故障单元,分别设置电阻和电容的正常容差为5%和10%.每个器件设置的故障阈值为±50%,即当这4个器件任何一个的参数值在其标称值±50%以外,则认为电路出现故障,本文只考虑单故障的情况.即电路总共有 R2↑(F1),R2↓(F2),R3↑(F3),R3↓(F4),C1↑(F6),C1↓(F7),C2↑(F8),C2↓(F9)这8种故障模式和1种正常模式(本文将正常情况也看成一种故障模式F5),共9种故障模式.其中↑表示器件参数超过标称值50%,↓表示器件参数低于标称值50%.

文献[10]指出,电阻R2阻值变大对电路的影响很小,F1和F5这两类故障模式的差异最大不超过8.5%,导致在实际的电路中,这两类故障模式很难区分.因此,本文将故障F1和F5合并为一类故障F5,并对这8类故障进行诊断.

图3 Sallen-key滤波电路原理图Fig.3 Circuit diagram of sallen-key filter

如图3所示,电路的激励信号为幅值 5 V、脉宽10 μ s的矩形信号.通过PSPICE对电路图进行仿真,对每种故障模式进行25次蒙特卡洛分析以获得故障诊断数据.其中15组用来训练神经网络,另外10组用来测试.

本文所采用的神经网络为BP网络,神经网络的结构为5-5-1,输入层有5个节点对应5维故障特征输入向量,输出层有1个神经元,输出数据1～9分别对应于9种故障模式(F1～F9).BP学习算法采用最速下降BP算法(matlab中用traingd函数表示),适应度函数为均方误差(mse)函数,目标精度为0.2.

利用标准BP算法和MDE算法分别对神经网络进行训练,两种算法对15个故障训练样本进行训练的时间与诊断结果对比如表1所示.

从表1可以看出,基于MDE算法的训练时间为BP算法的50%左右,训练速度明显快于BP算法,且训练效果也优于BP算法,体现出MDE算法在神经网络权值训练中具有较强的优越性.

利用训练好的两种神经网络对10个测试样本进行实际诊断,故障诊断准确率对比如表2所示.

表1 BP算法和MDE算法训练结果对比Tab.1 Comparision of trainging results with BP algorithm and MDE algorithm

表2 BP神经网络和MDE神经网络实际诊断结果对比Tab.2 Comparision of diagnosis results with BP neural network and MDE neural network

从表2可以看出,微分进化神经网络的故障诊断准确率要比BP神经网络高7%,充分验证了微分进化神经网络在故障诊断方面的优越性.

利用MDE优化后的神经网络对Sallen-key滤波电路各故障模式的具体诊断结果如表3所示,表3中每一行表示的是对某个特定故障类型进行诊断时,神经网络得到正确结果的样本数以及误判的样本数.例如,对于故障F3来说,10次诊断都获得了正确的结果,对于故障F6和F7来说,10次诊断中均出现了一次误判.

表3 基于微分进化神经网络的故障诊断结果Tab.3 Fault diagnosis results with differential evolution neural network

从表3可知,基于微分进化神经网络的故障诊断方法是有效的,并且表现出了优异的性能.

4 结 论

本文提出了一种在搜索过程中基于混合变异策略的微分进化改进算法,该算法在保证种群多样性的同时使得搜索速度有较大提高,同时本文利用改进的微分进化算法来训练神经网络权值.利用微分进化算法优化神经网络时,具有如下优势:①MDE算法在适应度函数的选取上没有太多的限制,而BP算法要求适应度函数是可微的;②基于微分进化的神经网络学习算法能够比较好的得到全局最优,且收敛时间相对较短,其综合性能明显优于BP算法.

最后,将微分进化神经网络用于模拟电路故障诊断,实验结果表明,基于微分进化神经网络模拟电路故障诊断方法与BP神经网络相比具有训练时间短、故障诊断准确率高的特点,为模拟电路故障诊断提供了新的思路和方法.此外,基于微分进化算法的神经网络结构优化也是有待进一步深入研究的课题.

[1]叶笠,王厚军,田书林,等.容差模拟电路软故障诊断的一种方法[J].电工技术学报,2011,26(5):119-125.

Ye Li,Wang Houjun,Tian Shulin,et al.An approach for soft fault diagnosis on analog circuits with tolerance[J].Transactions of China Electrotechnical Society,2011,26(5):119-125.(in Chinese)

[2]祝文姬,何怡刚,谢宏,等.基于遗传BP网络的模拟电路故障诊断[J].测试技术学报,2007,21(5):460-467.

Zhu Wenji,He Yigang,Xie Hong,et al.Fault diagnosis based on GA-BPNN for analog circuits[J].Journal of Test and Measurement Technology,2007,21(5):460-467.(in Chinese)

[3]张彦斌,贺从林,张鹏.基于神经网络的某装备电路单元故障诊断研究[J].测试技术学报,2010,24(6):558-561.

Zhang Yanbin,He Conglin,Zhang Peng.ANN-based fault diagnosis method of circuit units for a certain weapon equipment[J].Journal of Test and Measurement Technology,2010,24(6):558-561.(in Chinese)

[4]Yin Shirong.Application of BP Neural Network in Analog Circuits Diagnosis[C].Shanxi University.2010 International Conference on Computer Application and System Modeling,Shanxi:IEEE Computer Society,2010,V11:1140-1143.

[5]Blanco A,Delgado M,Pegalajar M C.A genetic algorithm to obtain the optimal recurrent neural network[J].International Journal of Approximate Reasoning,2000,23(1):67-83.

[6]Tan Yanghong,He Yigang,CuiChun,et al.A novel method for analog fault diagnosisbasedon neural networks and genetic algorithms[J].IEEE Transactions on Instrumentation and Measurement,2008,57(11):2631-2639.

[7]He Wuming,Wang Peiliang.Analog Circuit Fault Diagnosis Based on RBF Neural Network optimized by PSO Algorithm[C].IEEE Intelligent Computation Society.2010 International Conference on Intelligent Computation Technology and Automation,Changsha:IEEE Computer Society,2010,628-631.

[8]高海兵,高亮,周驰,等.基于粒子群优化的神经网络训练算法研究[J].电子学报,2004,32(9):1572-1574.

Gao Haibing,Gao Liang,Zhou Chi et al.Particle swarm optimization basedalgorithm for neural network learning[J].Acta Electronica Sinica,2004,32(9):1572-1574.(in Chinese)

[9]Rainer Storn,Kenneth Price.Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces[J].Journal of Global Optimization,1997,11(4):341-359.

[10]Farzan Aminian,Mehran Aminian,CollinsH W.Analog fault diagnosisof actualcircuits using neural networks[J].IEEE Transactions on Instrumentation and Measurement,2002,51(3):544-550.