基于固定尺度欧氏距离的变因子递推子空间辨识算法✴

黄金峰,张合新,张 植

(1.第二炮兵工程学院自动控制系,陕西西安 710025;2.第二炮兵驻二00厂军代室,北京 100854)

0 引 言

近年来,子空间算法[1,2]因对先验知识要求较少以及数值计算上的优势,对多变量系统辨识广泛适用,受到控制和辨识领域的广泛关注.随着对其研究的不断拓展,递推子空间辨识算法[3,4]也成为一个热点研究问题,并取得了一些成果[5-7].

Mercère G等[5]基于投影近似子空间跟踪(PAST)实现对SVD的更新,以递推方式获取扩展能观测矩阵并成功应用于Wiener系统的辨识,但由于投影的近似性,估计值不一定能收敛到真值.Oku H等[4]利用梯度型子空间跟踪算法实现了广义能观测矩阵的递推形式,但没有考虑引入遗忘因子机制.杨华等[6]提出一种新的梯度型递推子空间辨识算法,实现基于RLS-like遗忘因子数值Hankel矩阵的构造,提高了递推估计的辨识速度,但采用固定遗忘因子的方法,当A的特征值发生变化时,算法不能同时保证快速跟踪和跟踪效果.

本文以MOESP[5-7]中的OM算法为研究对象,针对一类时变系统,提出一种变因子递推子空间算法.该算法利用系统矩阵A的特征值空间欧氏距离[8,9]信息实现变因子的步骤,在保证跟踪效果的条件下提高了算法对参数变化的跟踪能力.同时针对变动检测中子空间跟踪问题中W的列向量可能出现不相交的情况,运用OPAST算法递推估计广义能观测矩阵,保证了W的列向量收敛于主子空间的正交基上.仿真结果验证了算法的有效性.

1 固定尺度的欧氏距离准则变因子递推OM辨识算法

考虑一类子空间模型:

式中:u(t)∈Rm,y(t)∈Rl,x(t)∈Rn分别为输入、输出和状态向量;w(t)∈Rn,v(t)∈Rl分别为过程和测量噪声.为保证系统的可辨识性和收敛性,假设满足(A,B)能控,(A,C)能观测,系统为最小实现;且外部输入和噪声不相关,输入满足充分激励条件.同时为研究简便,假设w(t)=0,即状态方程中不含过程噪声.

子空间辨识的本质就是直接从数据对中估计广义能观测矩阵,为此Verhaegen.M等设计了一系列的MOESP算法.本文在其中的OM算法(Ordinary MOESP)的基础上设计了基于欧氏空间变因子的递推子空间辨识算法,其步骤如下:

Step1:构造带有遗忘因子的Hankel矩阵:

给定初始输入输出数据对{ui,yi}(i=1,2,…,N),构造初始Hankel矩阵(以输入Hankel矩阵为例)[10]

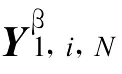
据式(3)形式,系统输入输出有如下关系:

Step2:OPAST[11]法更新广义能观测矩阵及估计系统参数矩阵:

在0(N序列)步,对数据矩阵进行QR分解

递推第1步,获取新的数据对后,对更新的增广数据矩阵做QR分解

经一系列Givens旋转,则式(8)R部分变为

R22(1)可以利用数据更新QR分解获得_

为实现广义能观测矩阵子空间的重构,首先对R22(0)进行SVD分解,则有

为递推更新(j),运用子空间跟踪问题,形成如下无约束最优化问题求解[12]

基于Yang的准则,形成了不同方法的递归计算W(j),如辅助变量PAST算法[13]和 IV-PAST算法[5].理论上,最小化准则J(W)中W的列向量是正交的,PAST算法指数级收敛于主子空间的正交基上;但在某些情况下,PAST算法将会在两个矩阵间来回摆动,这样就不会收敛于主子空间的正交基.文献[11]给出了这个问题的一个证明.如果W列向量不是正交的,这就表示在估计的过程中,不能够保证在同一状态空间坐标下的估计一致性,尤其是运用于变动检测上[3].为此,本文采用文献[11]提出的正交化PAST算法(简称OPAST算法),运用矩阵求逆引理得到W的最小二乘方法计算步骤

把上述的向量zj用Givens变换后的观测向量(j)代替,获得的W矩阵就是子空间辨识所需的广义能观测矩阵估计(j).变遗忘因子机制下输入输出Hankel矩阵不能直接用因子矩阵和数据矩阵乘积描述,应按式(14)近似处理.

因子.则有该机制下Hankel矩阵存在如下关系:

则矩阵估计^C(j)可直接从(j)中提取

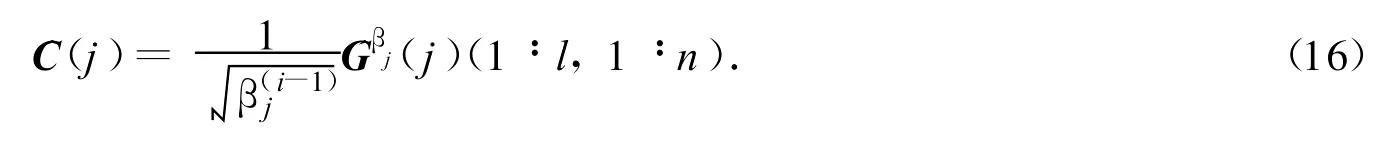
由式(15)可知,估计A^(j)有如下关系:

当遗忘因子β为固定值β0时,M(j)方阵就退化为.而矩阵B,D的估计值包含在矩阵(j)中,为得到其估计值,需从式(15a)中消去(j)(j)项.定义矩阵(j)为(j)的正交补,式(15a)两边左乘PG(j)右乘)可得

求解系统矩阵^B(j)和 ^D(j)估计的余下步骤见文献[10].

Step3:固定尺度欧氏距离准则更新遗忘因子:

采用遗忘因子方法进行递推计算的准则是:对快时变参数选较小的遗忘因子,而对慢时变参数选较大的遗忘因子.基于该准则,本文利用系统矩阵A的特征值空间欧氏距离大小来判断参数变化的快慢,但运用相邻估计距离差会因变因子更新频繁导致辨识精度变差.因此本文采用固定区间[(k-1)p+1,kp]内最大值和最小值的距离差来判断参数变化的快慢从而避免了变因子变化过于频繁,提高了算法的稳定性.令其中p表示固定步长,k=1,2,3,….即

这里λi为矩阵A的第i个特征值.利用上述的距离信息来更新遗忘因子 βj

式中:n为矩阵A的维数;c为弱化因子.βmin为遗忘因子的下限值.

2 数值仿真

仿真1:建立时不变仿真模型,选择系统矩阵参数为

仿真中采用方差为1的零均值白噪声作为激励信号,由四阶Butterworth滤波器产生,截止频率为0.8倍奈奎斯特频率,输出被不相关的零均值白噪声污染,信噪比为 25 dB.仿真参数为:N=20,i=3,βmin=β0=0.9.分别选择固定尺度p=2,5,20进行仿真.

图1表明:增加固定尺度p,变因子β越晚接近于1,跟踪越快,但跟踪效果越易受噪声影响.反之则 β越早接近于1,跟踪能力越慢,但跟踪效果越不易受噪声影响.仿真结果显示慢变系统辨识选择p=5较为合适.

仿真2:建立慢变模型,k＜1 000时模型参数同仿真1.k≥1 000时,A的参数为

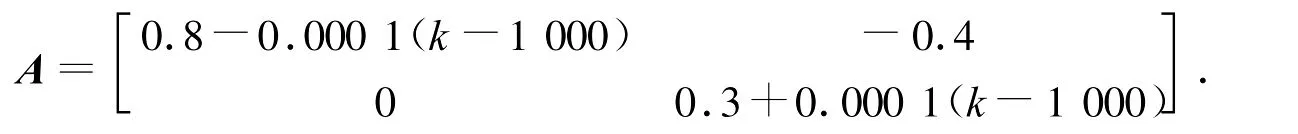
分别运用变因子法、不加遗忘因子和固定因子0.9进行了仿真.仿真结果如图2所示.

图1 时不变系统不同尺度跟踪曲线Fig.1 Different scales’parameters of time invariant system

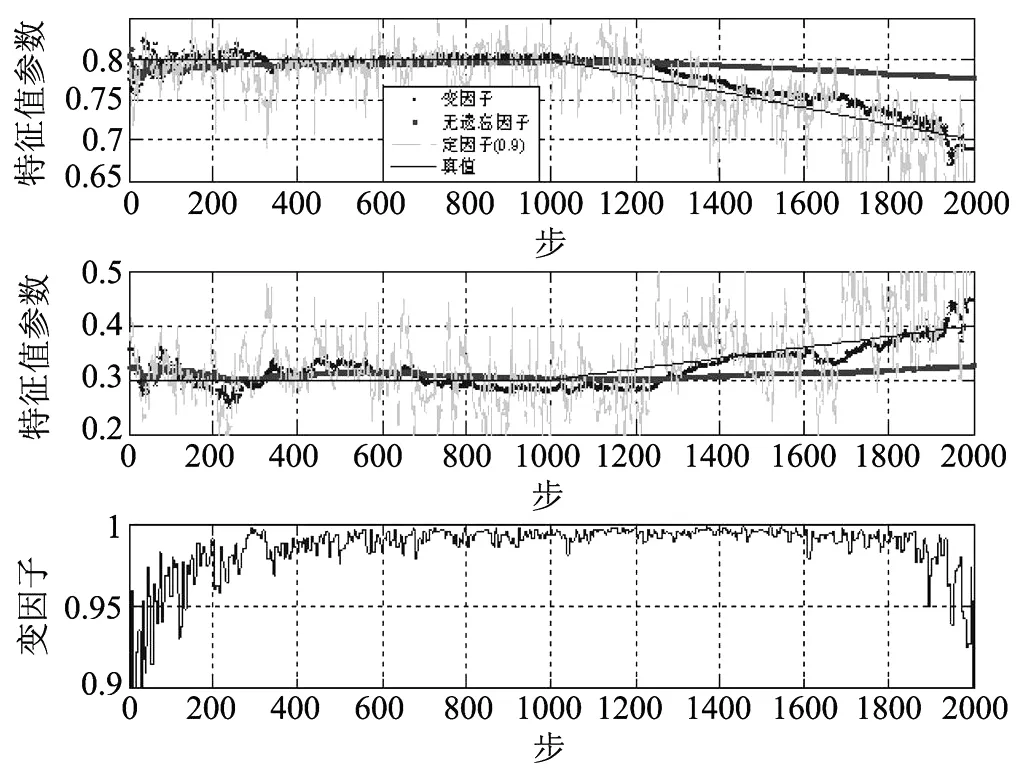
图2 时变模型不同方法辨识参数曲线Fig.2 Different identification methods parameters of Time-varying model

仿真2结果表明:对慢变系统定因子0.9法虽能够较好地跟踪曲线变化,但跟踪精度差;无遗忘因子的稳定性较好,但在参数发生变化时,跟踪速度慢;而本文研究的固定尺度变因子法不但保持了较好的跟踪速度而且保持了较好的跟踪效果.

3 结 论

本文针对传统的OM子空间辨识算法采用固定遗忘因子方法进行变动检测时不能同时保证快速跟踪和跟踪效果等问题,提出了一种基于欧氏距离的变因子递推子空间辨识算法.该算法分为 3个步骤:首先引入变因子构造与更新Hankel矩阵和观测向量;其次为保证广义能观测矩阵的列向量收敛于主子空间的正交基上,采用OPAST算法递推估计广义能观测矩阵,并由广义能观测矩阵估计系统参数矩阵;最后用的特征值空间距离信息实现变因子,此算法具有的自适应能力.应用于一类时变系统,仿真结果验证算法的有效性.

[1]Trnka P.Subspace like identification incorporating prior information[J].Automatica,2009,46(4):1046-1091.

[2]杨华,李少远.一种完全数据驱动的子空间辨识与鲁棒预测控制器设计[J].控制理论与应用,2007,24(5):732-736.

Yang Hua,LiShaoyuan.A novel robust predictive controller design based on data-driven subspace identification[J].Control Theory&Applications,2007,24(5):732-736.(in Chinese)

[3]Mercère G,Bako L,et al.Propagator-based methods for recursive subspace model identification[J].Signal Processing,2008,88(3):468-491.

[4]Oku H,Kimura H.Recursive 4SID algorithms using gradient type subspace tracking[J].Automatica,2002,38(6):1035-1043.

[5]Lovera M,Gustafsson T,Verhaegen M.Recursive subspace identificationof linear and non-linear Wiener state-space models[J].Automatica,2000,36(11):1639-1650.

[6]杨华,李少远.一种新的基于遗忘因子的递推子空间算法[J].控制理论与应用,2009,26(1):69-72.

Yang Hua,Li Shaoyuan.A novel recursive MOESP subspace identification algorithm based on forgetting factor[J].Control Theory&Applications,2009,26(1):69-72.(in Chinese)

[7]Bontempi G,Birattari M,Bersini H.Lazy learning for local modeling and control design[J].International Journal of Control,1999,72(7/8):643-658.

[8]郑建柏,朱永利.基于欧氏聚类和支持向量机的变压器故障诊断[J].电力科学与工程,2008,24(4):13-15.

Zheng Jianbai,Zhu Yongli.Transformer fault diagnosis based on Euclidean clustering and support vector machines[J].Electric Power Science and Engineering,2008,24(4):13-15.(in Chinese)

[9]Zheng W X.Parameter Estimation of Stochastic Linear Systems with Noisy Input[J].International Journal of Systems Science,2004,35(3):185-190.

[10]Zhang C,Bitmead R.Subspace system identification for training-based MIMO channel estimation[J].Automatica,2005,41(9):1623-1632.

[11]Abed-Meraim K,Chkeif A,Hua Y.Fast orthonormal PAST algorithm[J].IEEE Signal Processing letters,2000,7(3):60-61.

[12]Yan F B.Asymptotic convergence analysis of the projection approximation subspace tracking algorithms[J].Signal Processing,1996,50(1/2):123-136.

[13]Gustafsson T.Instrumental variable subspace tracking using projection approximation[J].IEEE Transactions on signal processing,1998,46(33):669-681.