水面浮运铺设的机动管线有限元分析

文/张润波 彭 路

水面浮运铺设的机动管线有限元分析

文/张润波 彭 路

对管线进行有限元分析，了解其变形和应力分布状况，探讨管线的薄弱环节和确定危险应力处，对浮运时机动管线的变形和应力分布状态进行较为详细的分析。这为施工人员针对管线的薄弱环节采取必要的措施进行加强、确保管线施工安全有积极的指导作用。

机动管线；水面浮运；有限元模型；有限元分析

1.管线基本假设

管线水面浮运，在其刚被拉到对岸时受力最复杂，针对管线此时的状态进行有限元分析。在针对穿越连接器连接的DN100机动管线进行有限元分析时，为方便建立模型可做一些简化，忽略次要、影响不大的因素，使管线简化成承受轴向拉力和弯矩的柱梁。

（1）不考虑管线连接器对管线系统的影响，认为管线的抗弯刚度在纵向是均匀的。

（2）横截面上的抗弯刚度即应力应变关系保持不变，为定值。

2.管线铺设三维有限元模型的建立

2.1 单元类型的选取

本文采用的是固体 SOLID45 结构实体单元， SOLID45 单元主要用于模拟三维实体结构，由8个节点定义而成，每个节点具有3个自由度（分别是 UX、UY、UZ）。该单元适合于进行弹性、蠕变、膨胀、应力硬化、大变形、大应变的分析，具有退化功能，可退化成五面体和四面体，便于生成复杂结构的单元网格。

2.2 材料特性

管线的抗弯刚度在纵向是均匀的，因此铺设的管线采用同一种材料，且浮运时重力与浮力相抵消，故不用对材料的密度进行设置。

弹性模量E=2.2e11pa

泊松比μ=0.3

2.3 三维实体模型的建立

本文采用实体建模的方法。管线的几何参数如下：

管道的内半径Ri=0.0485m

管道的外半径Ro=0.051m

实体模型的长度L=50m

2.4 网格划分

建立实体模型之后，进行网格划分，生成有限元网络图，在Z轴方向上将线段200等分，在端面圆周上将线段10等分，然后用m esh工具对整个实体模型进行网格划分，划分网格后单元和节点的情况如下：单元共计18000 个，节点共计24120 个。图1为形成的图1A区域的有限元网格图。

图1 管线局部有限元网格图

在现实情况下，管线约束情况比较复杂，其两端都有钢丝

2.5 载荷与边界条件绳提供拉力，若管线两端一端全约束，另一端约束X、Y方向，则两端变形及应力状态相比差别较大，不符合实际情况；若两端都只固定X轴、Y轴方向，使其在Z轴自由，则软件无法计算结果，因此约束条件为在管线两端都采用全约束，比较符合管线实际情况。

3.管线变形及应力分布

3.1 管线变形

对模型求解，得到管线变形和未变形图如图2。

图2 管线变形及未变形图

从图2可以看出，管线在Y、Z轴没有位移，X方向发生了位移，管线靠近两端处位移较小，越靠近管线中间，位移越大，在中间位置位移达到最大的3.092m。

从有限元分析结果来看，位移变化趋势是正确的，管线两端全约束，故靠近两端处位移小，越靠近管线中间，变形越大，但是3.092m的位移有些偏大，究其原因，50m或更长的管线在受到均布载荷后，会发生大变形等几何非线性行为，即应力应变关系会随着管线的形状发生变化，而分析时假定其是线性的，故导致管线最大位移有些偏大。

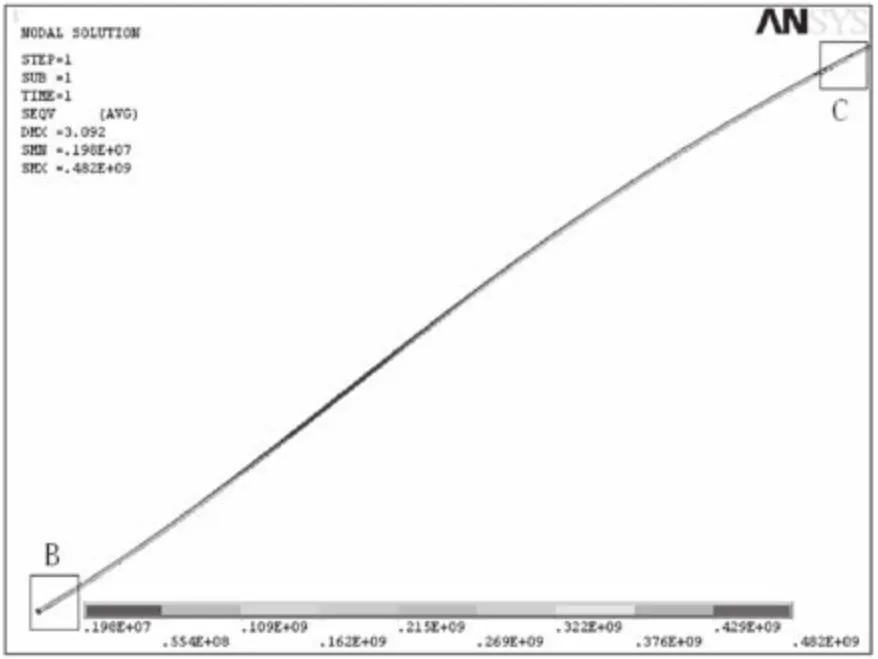
图3 25-50m管线应力分布图

3.2 应力分布

建立的有限元模型可知，管线两端约束条件相同、载荷为均布载荷，因此管线的应力分布状况以管线中间（Z=25m）为中心呈对称分布，图3为求解后25m～50m的管线应力分布图。

从图3可以看出，管线的应力分布状况从管端到中间应力是由小骤增至最大应力，后逐渐变小到最小值，将要到达管线中间时应力又增大到一较大值。图4和图5更清晰地反映了管线端部B区域和中间C区域的应力分布。

图4 管线端部（B区域）应力分布图

图5 管线中间（C区域）应力分布图

从图4可以看出，管线的最大应力处是靠近管线端部迎着水流方向的一小段，其应力值达到0.482e9pa，这是因为管线两端都是全约束，在靠近端部的地方会产生较大的应力使得管线不发生位移和转动，此处在铺设时应高度重视，采取措施确保应力不超过管线允许应力。

从图5可以看出，管线中间迎着水流方向的一段应力也比较大，达到0.322e9pa，管线在均布荷载的作用下，此处是管线位移最大的地方，因此会产生较大的弯曲应力，也应当给予重视。

4.结语

本文针对铺设管线的类型做了一些假设，建立了水面浮运铺设管线的实体模型和有限元模型，并进行了计算，计算结果显示，管线中间处位移最大，但因没有考虑非线性因素，导致位移偏大，管线在靠近两端处应力最大，在中间处也有较大的应力，因此在铺设中应对这几处给予足够的重视。

广西贵港市75130部队后勤部）