地下工程电渗透防渗防潮技术理论研究

文/何静波 何国杰

地下工程电渗透防渗防潮技术理论研究

文/何静波 何国杰

地下工程渗漏、潮湿问题对结构本身和室内设施设备具有严重的破坏作用，传统防渗防潮技术无法解决根本问题，电渗脉冲防渗防潮技术优势明显。本文重点针对电渗法应用于地下工程防渗防潮的传质及电渗流的机理进行分析，建立外加电场作用下的渗流流速模型，并作简要理论分析。

地下工程；电渗透；防渗防潮

21世纪被普遍认为是人类开发和利用“地下空间”的世纪。然而，地下水渗漏、空间潮湿是地下工程使用和维护管理过程中不可避免的问题，渗水锈蚀混凝土钢筋。腐蚀机器设备，恶化空气质量。目前，主要防水技术有防水混凝土防水法、涂刷防水涂料法、覆盖防水卷材法、外部排水管排水法等，地下工程防潮则主要依靠除湿机进行空气置换。这些方法不够彻底、维修成本高、使用寿命短。电渗透防渗防潮技术，基于电渗原理，外加电压产生电势差，促使阳离子带动水分子向阴极流动，实现防渗防潮的目的。在国外地下工程的应用显示该系统优势明显，持久有效，便于安装，维护成本低，使用安全。

1.电渗机理

1809年，俄国科学家F.F. Reuss在实验中首次描述了电渗现象。在外加电场作用下，水分子能够通过毛细管移动。以后的研究表明，流动最早是由多孔介质中的阳离子（带正电的离子）的运动开始，附着周围的水分子随着流动。

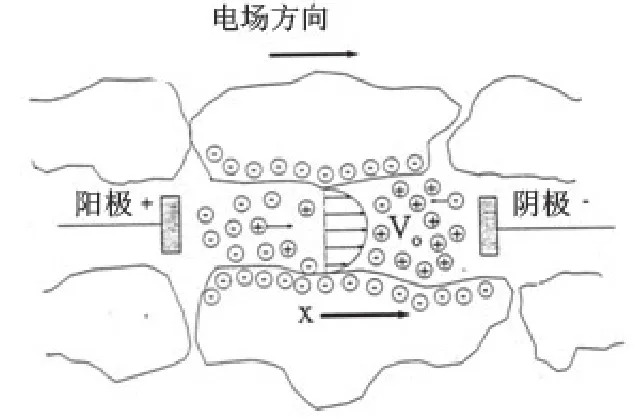
图1 电渗原理示意图

1.1 双电层理论

双电层模型是由Quinke首先独立提出的，Helmholtz于1879年正式在该模型的基础上给出了电渗现象的理论模型，后来的研究又补充提出了扩散双电层模型。电渗现象是基于双电荷层原理，即同一符号的离子层被稳固地吸附到固体表面或微粒上。整体呈电中性，而且在离子附近区域存在相同数量的相反电荷，即随着距离的增加电性逐渐减弱，称为扩散层。当固体表面和液体处于相对运动的状态，就存在流速梯度，溶液的薄层和其上离子在墙体附近固定不动。部分离子随着溶液移动，一部分（被吸附的离子）离子吸附在表面。因此，液相和墙体有不同的净电荷而且在外部电场的作用下产生相对运动。

图2 Helmholtz双电层模型

1.2 电渗传质机理

通过在多孔介质中植入电极，可以产生电势梯度，对多孔介质内孔隙自由水中离子和扩散层中的可交换离子产生影响。在电渗流中，带电粒子的移动通过粘滞力带动孔隙水移动。通常情况下，介质颗粒所带的净电荷是负的，所以双电层中所存在的净电荷是正的。对于静止的介质颗粒来说，双电层中的孔隙水流是向阴极方向的。双电层中的水的流动将会对孔隙中的自由水产生粘滞力。实际上，孔隙中液体流动有时仅仅是由于含水离子的移动所引起。

在持续不变的电渗流中，在正极附近发生了氧化反应，产生了新的阳离子，从正极附近溶液进入到电渗系统，逐渐占据了原来阳离子的位置。带电离子的定向移动，使得正极附近聚积了阴离子，负极附近聚积了阳离子，由此而产生了电动电势，形成了电渗阻力效应，减缓了原有电渗作用效果。

1.3 电渗流速机理

电渗流的流速依赖于双电层中离子移动的能力，主要受电势梯度影响，同时也和介质表面的相互影响程度有关。固定层离子的移动能力随着与介质表层距离的增加而增加，逐渐达到一个常数。

在介质的固定层内离子在动电过程中通常被认为是不动的。固定层离子被复杂的共价键和离子键束缚在其范围内部，在外部则靠着电场力来对离子保持着影响。在介质当中，微粒表面的电荷是微不足道的，离子可以通过细微的联通孔隙移动。因此，电传导的主要影响因素有孔隙中的自由水、孔隙率、饱和度，在细粒介质中电传导性交得更加复杂。

根据欧姆定律，影响电渗作用效果的3个实质因素是：级间电压、级间电阻（电极电阻、介质电阻和界面电阻）和电渗电流。介质中电流传导是一个涉及电极间氧化还原反应的复杂过程，与双电层中孔隙自由水移动能力密切相关。

2.稳态条件下单相流体电渗模型

在外加电场作用下，极性流体在渗流过程中要受到电动力、粘滞力、重力、电动阻力的共同作用。在多孔介质的毛细管中，液体运动的基本方程如下：

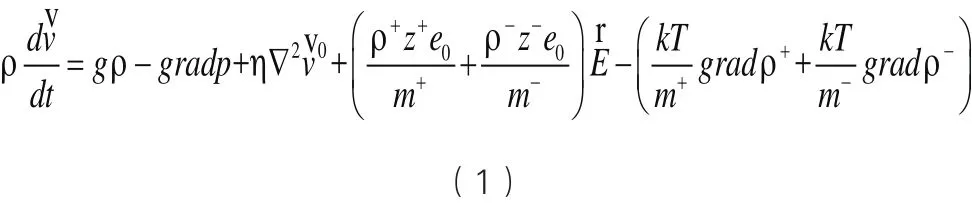
其中：ρ为液体的密度，ρ±为正（负）离子的密度，为液体的速度，为溶液的速度，g为重力加速度，p为压力，η为剪切粘度系数，z±为离子电荷，e0为基本电荷，m±为离子质量，为外加电场强度，k为玻尔兹曼常数，T为温度。可以看出，式（2）右边由以下因素组成：重力、压力、粘滞阻力、电动力、温度合力。

采用J.Kozeny建立的毛细管岩石模型，作如下假设：①渗流速度足够小，流体流动为线性渗流；②忽略电场作用引起岩石性质变化；③流体不可压缩；④扩散双电层很薄,远小于毛细管半径；⑤无源和汇存在。此外，还要忽略流体中带电离子之间的相互作用。由Helm holtz—Sm oluchow ski方程，单根毛细管的电渗流速ve

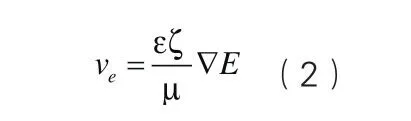
其中ve为电渗流速，cm/s；ε为流体的介质常数；ζ为动电电位，m V；μ为流体的黏度，m Pa·s；E为外加电位，V。

假设多孔介质由n根弯曲毛细管组成，根据多孔介质特性，式（3）表示为

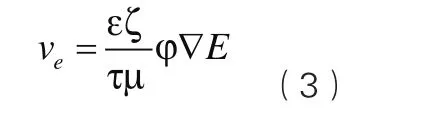
其中，τ为迂曲度，φ为多孔介质孔隙度。

根据渗流基本理论，对于各项同性介质中单相流体的渗流满足达西定律

式中vh为水力梯度作用产生的渗流流速；k为多孔介质的渗透率，μm2；p为压力。

由式（4）和（5）可得，在水力和电渗耦合作用下的耦合流速

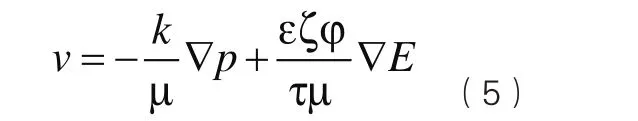
由能量守恒原理，渗流连续性方程为

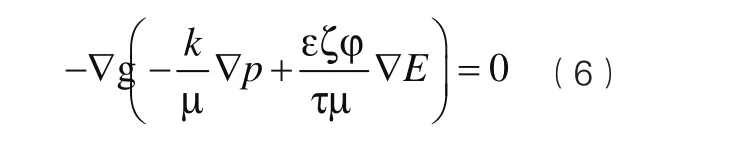
式（6）即为稳定状态下单相流体的水力和电渗耦合作用下的渗流模型，该微分方程可以用有限元方法进行求解，求得模型的压力分布及流速值，进而可以通过数值模拟得到近似的渗流流速与压力、电位之间的关系曲线。

3.理论分析

由式（1）和（6）可以知道，外加电场作用下极性流体的渗流速度除与压力、重力、粘滞阻力有关外，还与外加电场的电压和正负电极之间的间距有很大的关系。另外，外加电场强度是有方向性的，因此，流体的渗流速度与外加电场的方向有关。从理论的角度讲，当外加电场的方向与水力梯度的压力方向一致时，渗流速度会明显加快；当方向相反时，渗流流速会减缓，外加电场作用强度足够平衡或超过水力梯度时，渗流就会停止甚至反向。但在实验研究过程和工程实践应用中，还有很多因素影响其作用，如电极与土体之间的界面电阻、外加电场对流体粘度的影响、电极的电化学反应形成附加电阻和电荷累积等等，通过对诸多因素影响电渗作用规律的研究，进一步修正电渗流速方程，国内部分学者已经开始着手相关方面的工作。

解放军后勤工程学院）