基于Petri网理论的自动化立体仓库建模

文/周 文 吴晓波 陈 遥

基于Petri网理论的自动化立体仓库建模

文/周 文 吴晓波 陈 遥

针对自动化立体仓库的离散事件系统建模，Petri网理论具有自身的优势，但在建模时可能存在“组合爆炸”问题。本文以某自动化立体仓库为例，采用了分解系统和复合模型的建模方法，不但保持了Petri网的分析和验证能力，而且避免了“组合爆炸”问题。

自动化立体仓库；Petri网；组合爆炸；复合模型

对系统进行建模与仿真，首先要建立一个有效表达系统的理论模型，如果模型不正确或者不理想，仿真就失去了意义。所以选择一个有效的理论建模方法并且能很好地使用此建模方法，这对自动化立体仓库的建模仿真极其重要。Pe tri网是一种结构化的离散事件系统描述工具，能够充分显示离散事件系统局部之间的关系[1,2]。自动化立体仓库系统是典型的离散事件系统，Pe tri网对其建模非常合适[3,4]。

1.Petri网理论在离散事件系统建模中的优势

现有主要的理论建模方法包括实体流图法、活动周期图法、Eule r网方法和Petri网方法。

实体流图法以临时实体产生、流动、消亡及其经历永久实体服务的过程为主线，建立系统的工作流程和实体之间的逻辑关系，具有简便易行的特点，是一种最基本的建模方法。活动周期图法针对实体的行为模式和活动逻辑进行建模，可以直观地表示各类实体在其生命周期中的活动和状况变化，清晰地描述实体之间的关系。Eu le r网方法同时具备活动周期图和Pe tri网方法的基本特点，在连续与离散事件混合系统建模方面的能力比较强[5]。

Pe tri网方法比较严密规范，并可借助数学方法对系统中发生的并发、冲突和死锁等现象进行分析。Pe tri网是一种用简单图形表示的组合模型，具有直观、易懂和易用的优点，它能够较好地描述系统的结构，表示系统中的并行、同步、冲突和因果依赖等关系，并以网图的形式，简洁、直观地模拟离散事件系统，分析系统的动态性质[2]。以上建模方法适用范围不同，都存在优缺点，Pe tri网方法在自动化立体仓库有一定的优势。但它有局限性，如果对象是一个复杂的大系统时，Petri网规模庞大，可能会引起“组合爆炸”问题[6]，给分析带来困难，为了发挥其优点消除缺点，本文针对自动化立体仓库的建模工作主要在Pe tri网理论上，采用分解系统和复合模型的建模方法。

2.基于Petri网的自动化立体仓库建模步骤

（1）系统调研。对系统调研，了解系统运行状况和采集系统数据资料的过程，深入了解系统的总体流程、各种建模参数，以便建立系统模型。

（2）分解系统。把整个系统分解成若干个子系统，以便对它们分别进行建模分析。

（3）复合建模。建立对象模型、建立Petri网图、建立系统变迁事件表和建立系统Petri网可达树。

（4）分析模型。通过以上模型的建立，可以分析自动化立体仓库系统能否顺利作业，有无瓶颈、死锁等状况发生。

通过以上步骤对自动化立体仓库进行Petri网建模不但达到建模的目的，而且可有效地避免“组合爆炸”等问题的发生。

3.Petri网方法的应用举例

某企业刚新建了一个自动化立体仓库，该自动化立体仓库主要储存托盘物料。

3.1系统调研

通过系统调研，对整个系统有了比较深入的了解，整个系统可分为入库作业系统、拣选作业系统、出库作业系统。以入库作业为例，需要入库的货物卸货完毕后进行人工组盘，人工组盘后以托盘形式进行货物的存储。托盘被叉车搬运到入库站台，进行信息录入、读RFID等入库操作，在处理过程（如：重量检测、尺寸检测等）中如发现问题应进行人工整理，然后再次进行刚才入库处理作业。相关作业处理完毕后，输送系统将托盘运到自动化立体仓库堆垛机取货台，准备入库。该立体仓库入库流程如图1所示。

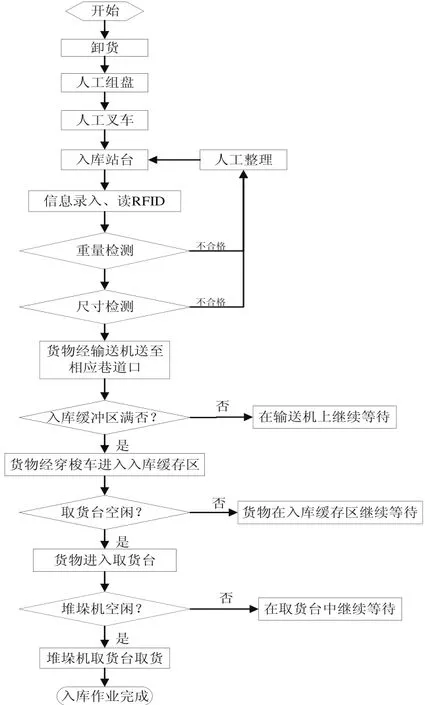
图1 自动化立体仓库入库流程图

3.2分解系统

将各系统分解成子系统，以便后面复合建模。以入库作业系统为例，将入库作业系统分为进货子系统和储存子系统。

3.3复合建模

对各子系统进行复合建模，即建立对象模型、建立Petri网图、建立系统变迁事件表和建立系统Petri网可达树。以入库作业系统的进货子系统为例进行复合建模，根据自动化立体仓库设备关系，建立该自动化立体仓库进货子系统的对象模型。其中：

P={p1,p2, …,pm}是有限库所节点的集合，m≥0。T={t1,t2, …,tn}是有限变迁节点的集合，n≥0。对象模型如图2所示。

图2 自动化立体仓库进货子系统对象模型

根据该自动化立体仓库进货子系统对象模型建立该自动化立体仓库进货子系统的动态Petri网模型，如图3所示。

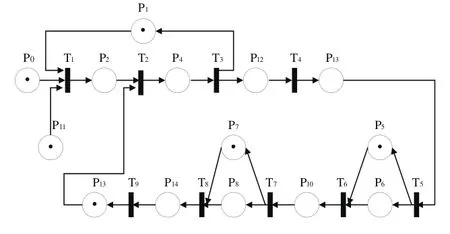
图3 自动化立体仓库进货子系统Petri网模型

模型中各个库所与变迁的含义如表1所示：

表1 进货子系统的库所与变迁含义

根据自动化立体仓库进货子系统Pe tri网模型，得到子系统的变迁事件表，如表2所示。

表2 自动化立体仓库进货子系统层的变迁事件表

为了建立该模型的可达树，把物流层和信息管理层统一标识为：Mn=（p0,p1,p3, …,p13,p14）。由自动化立体仓库进货子系统Petri网模型，可得初始标识M0=（1,1,0,1,0,1,0,1,0,1,0,1,0,0,0），分析P e t r i网模型，论证是否存在变迁序列使得目标标识Mz= M0=（1,1,0,1,0,1,0,1,0,1,0,1,0,0,0）可达。

经过对该自动化立体仓库进货子系统Petri网模型分析，得到可达树如图4所示。

从可达树中发现，初始标识M0=（1,1,0,1,0,1,0,1,0,1,0,1,0,0,0）经过变迁序列σ=T1T2T3T4T5T6T7T8T9到达了目标标识Mz=（1,1,0,1,0,1,0,1,0,1,0,1,0,0,0）= M0，即回到了初始状态。这说明，该自动化立体仓库进货子系统的Pe tri网模型是可达的、畅通的，货物和信息都能顺利到达理想位置，进货作业可以顺利进行。

图4 自动化立体仓库进货子系统可达树

4.结论

本文采用了分解系统和复合模型的建模方法，不但保持了Pe tri网的分析和验证能力，而且避免了基本Petri网“组合爆炸”现象的发生。通过实例验证了该方法的有效性，从而达到了研究自动化立体系统能否顺利作业，有无瓶颈、死锁、冲突等状况发生的目的，进而对系统进行下一步仿真打下基础。

[1]易继锴,侯媛彬.智能控制技术[M].北京：北京工业大学出版社,2007:23-29.

[2]袁崇义.Petri网原理与应用[M].北京：电子工业出版社.2005.3.

[3]田宝,祝中华.基于着色赋时Petri网的自动化立体仓库系统建模[J].工业自动化,2008,37(2):34-38,63.

[4]SU Yong-ding,Q IU Jing,LIU Guan-jun.M odeling o f testab ility requ irem en t based on generalized stochastic Petri nets[J].Joum al of China O rdnance,2009,1:60-64.

[5]王维平等.离散事件系统建模与仿真（第二版）[M].北京：科学出版社.2006.

[6]肖田元,范文慧. 离散事件系统建模与仿真[M].北京:电子工业出版社.2011.8.

解放军后勤工程学院）