复合材料蜂窝夹芯结构低速冲击位置识别研究

赵林虎，周 丽

(南京航空航天大学 飞行器结构力学与控制教育部重点实验室，结构强度研究所，南京 210016)

复合材料蜂窝夹芯结构由上下两块强度很高的复合材料层合板面板，以及面板间比重轻、尺寸较厚、承载能力相对较弱的蜂窝芯体组成。复合材料蜂窝夹芯结构具有极高的比强度和比刚度，被广泛的应用于航空航天飞行器结构，如机翼、地板等大部件［1－2］。但复合材料蜂窝夹芯结构抗冲击能力较差，在实际服役中遇到诸如修理工具掉落、冰雹撞击等低速冲击事件，虽然冲击能量不是很高，在面板上也难留下能观察到的痕迹，但仍可在结构内部造成蜂窝芯体塌陷、复合材料面板纤维断裂、蜂窝芯体与面板脱胶等低速冲击损伤，导致结构强度和稳定性的急剧下降［3］。如何有效的对复合材料蜂窝夹芯结构上的冲击载荷进行识别，一直是人们关注的焦点和难点。

近年来在智能材料结构及相关领域取得的新进展，使得利用集成在结构中的先进传感/驱动元件网络，在线获取与结构状态相关的信息，识别结构的安全状况成为可能。复合材料结构冲击载荷识别属于一种被动的结构健康监测方法，它的一个重要方面就是冲击位置识别。准确识别冲击位置有助于确定可能损伤位置，加速对结构重点部位的检测。目前在这个领域已研究探讨了一些技术方法，如神经网络方法、解析方法以及最优化方法等，虽然这些技术方法在一定程度上取得了成功，但它们或者需要大量的训练数据，或者需要特定模型，并且都是针对平板等简单结构［4－5］。一种较好的确定冲击位置的方法是对冲击引起的应力波进行分析，提取应力波的到达时刻，根据距离、时间和速度三者的关系计算出冲击位置［6－7］。但在复合材料蜂窝夹芯结构中，由于各向异性的特点，应力波的速度随传播角度而变换，因此不能简单地通过时间—路程关系来识别冲击载荷位置，因此有必要对复合材料蜂窝夹芯结构冲击载荷识别进行进一步的研究。

本文提出了一种基于应力波和免疫遗传算法的方法对复合材料蜂窝夹芯结构上的低速冲击载荷进行分析和定位。首先通过一组事先确定冲击位置的低速冲击载荷产生的冲击应力波实验数据获取了多个频率上冲击应力波在蜂窝夹芯结构中的传播速度;然后考虑冲击应力波的各向异性特性，采用免疫遗传算法对未知的低速冲击载荷进行位置识别。进行了实验研究来表明该方法的可行性和有效性。

1 冲击位置识别方法

当冲击载荷作用在结构上时，就会产生冲击应力波在结构中传播。在复合材料蜂窝夹芯结构中，由于各向异性的特点，应力波的速度随传播角度而变化。同时，应力波的频散特性又使得速度随频率而变化，因此难以像各向同性材料那样获得时间—路程的解析关系来简单识别冲击位置。在本文中，将冲击位置识别问题转化为一个对目标函数的优化问题。通过比较理论计算和实际测量的冲击应力波到达时间，采用免疫遗传算法对冲击位置进行识别。

在本文中通过最小化目标函数E来确定冲击载荷的作用位置，目标函数E的定义为:

式中n为传感器数量，ti和tj分别表示实验中实际冲击载荷应力波信号到达编号为i和j传感器的到达时间，t'i和t'j分别表示冲击载荷作用在假设位置时，冲击应力波传播到编号为i和j传感器的到达时间，t'i定义为:

式中(x，y)和(xi，yi)分别为免疫遗传算法中假定的冲击载荷作用位置和标号为i的传感器坐标，Cg(θ，f)是随角度θ和频率f变化的波速。在本文中，由于复合材料蜂窝夹芯结构的材料性质未知，难以采用理论或数值方法建立应力波群速度的分布，因此采用实验的方法对冲击载荷(作用位置事先确定)产生的应力波信号进行分析获取应力波的群速度分布。

采用免疫遗传算法后，最小化目标函数E的问题，可以转化为最大化聚合适应度函数F:

式(4)中k为免疫遗传算法常数，Ci为抗体浓度。当预测位置越靠近冲击载荷作用的真实位置，聚合适应度越大。本文基于免疫遗传算法的冲击载荷位置识别的流程图如图1所示。

图1 冲击载荷位置识别流程图Fig.1 The process of the impact location identification

2 冲击应力波信号时频分析

为了测量冲击应力波的波速及对冲击位置进行识别，需要获得冲击应力波从冲击点到传感器的传播时间。但应力波的频散性使得直接在时域准确测定其传播时间非常困难。时频分析方法能同时捕捉信号在时域和频域的特征信息，被越来越多地用于应力波的分析中。小波变换是被广泛应用在各个领域的一种成功的时频分析方法，在对应力波的分析中也表现出了良好的性能。因此本文采用Gabor小波函数对冲击应力波在时频域进行分析，以获取冲击应力波在不同频率上到达传感器的时刻，从而计算传播时间。

Gabor小波函数在时域和频域的定义分别为［8］:

使用Gabor小波函数对一沿x方向传播的由两个频率略有差别的单位谐波组成的频散应力波:

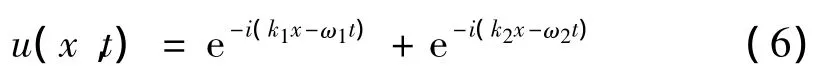
进行小波变换。当Δω非常小的时候，可得到小波系数的幅值为:

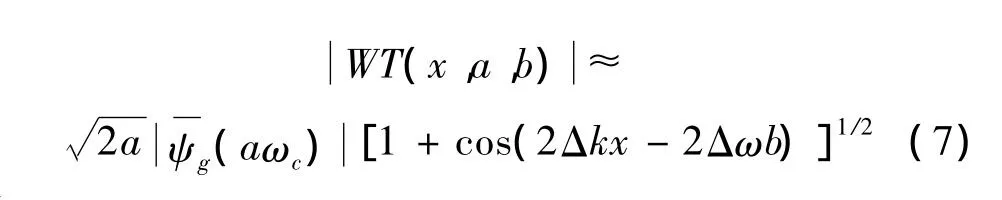
式中 Δk=(k1－k2)/2，Δω =(ω1－ω2)/2。式(7)的物理意义是:在时频域应力波的小波系数的幅值在圆频率ωc=ω0/a，即频率f=1/a处的峰值对应应力波群速度的到达时刻［9－12］，这样就可以在时频域准确确定冲击应力波的传播时间，并可根据已知的冲击点与传感器之间的距离，计算出冲击应力波的实际传播速度。

3 免疫遗传算法及实现

免疫遗传算法是基于生物免疫机制提出的一种改进的遗传算法，它将实际求解问题的目标函数对应为抗原，而问题的解对应为抗体。抗体与抗体之间也相互促进和抑制，以维持抗体的多样性及免疫平衡，这种平衡是根据浓度机制进行的，即抗体的浓度越高，则越受抑制;浓度越低，则越受促进，体现了免疫系统的自我调节功能，与生物免疫系统的功能相对应。基于免疫原理的遗传算法与标准遗传算法相比，因其具有免疫记忆功能并能自我调节，所以提高了算法的总体和局部的搜索能力，并能避免陷入局部解，并且提高了算法效率，减少了迭代次数［13－14］。

假设免疫系统由M个抗体(本文中抗体就是冲击载荷位置的编码)组成，每个抗体基因长度为N，采用符号集大小为S(对二进制编码，S=2，即采用0，1两种字符)。则在进化过程中，由抗体组成的免疫系统的不规则度(即多样度)可由 Shannon的平均信息熵H(M)表示，即:

式中Hj(M)为第j个基因的信息熵，定义为:

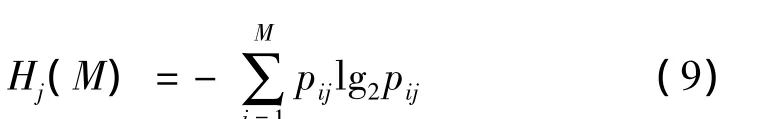
式中pij为第i个符号出现在基因座j上的概率。整个种群的相似程度可表示为:

A(M)表征了整个群体的多样度，A(M)越大，群体多样度越低，反之亦然。

在免疫遗传算法中，需要不断地计算个体的聚合适应度。聚合适应度实际是对适应度进行修正，修正方式如式(4)所示，式中抗体浓度Ci是指抗体在群体中与其相似抗体所占的比重，即

其中λ为相似度常数，一般取为0.9≤λ≤1。对最大优化问题，k取负数(本文中k= －0.8)。当进行选择操作时，抗体被选中的概率正比于聚合适应度。即当浓度一定时，适应度越大，被选择的概率越大;而当适应度一定时，抗体浓度越高，被选择的概率越小。这样既可保留具有优秀适应度的抗体，又可抑制浓度过高的抗体，形成一种新的多样性保持策略。当计算得到种群个体聚合适应度后，种群就可以根据聚合适应度进行选择，交叉，变异计算，进化出下一代种群，直到满足收敛条件。

4 实验研究

4.1 实验装置

为验证本文所提出冲击位置识别方法的可行性和有效性，对一复合材料蜂窝夹芯结构进行了实验研究。蜂窝夹芯结构如图2(a)所示，该结构由上下两块碳纤维复合材料蜂窝夹芯板和铝合金夹头组成，蜂窝夹层板为梯形，板厚24 mm。在结构的一个表面布置了4个直径为12 mm，厚度为1 mm的压电陶瓷片传感器组成如图2(b)所示的监测网络用于感知冲击载荷引起的应力波，并由NI PXI－4472数据采集卡获取以作进一步分析和处理。

图2(a) 实验装置图Fig.2(a) Experimental set-up

图2(b) 实验件尺寸Fig.2(b) The dimension of the experimental sample

4.2 波速曲线的获取

在对未知冲击载荷进行识别之前，先要得到结构中应力波随角度变化的波速曲线。在实验件上以传感器1为圆心，画一个直径为36 cm的圆，用力锤每隔5°在该圆上做低速冲击，对测量得到的冲击应力波信号进行小波分析，获得应力波的到达时刻，计算出每个角度上不同频率的传播速度，最后用多项式拟合得到应力波随传播角度变化的波速曲线。

图3(a) 应力波信号及300 Hz下的小波变换图Fig.3(a) The signal of the stress wave and wavelet transform(300 Hz)

图3(b) 应力波信号小波变换时频图Fig.3(b) The wavelet transform of the signal

图3(a)和图3(b)所示为其中一组应力波信号及小波变换时频图。从图3(b)可以看出，低速冲击载荷在该蜂窝夹芯结构上产生的应力波信号能量主要集中在0 Hz到500 Hz。根据小波变换可以提取出该频率范围内多个频率处应力波的到达时刻。如图3(a)中所示的波峰即为300 Hz处的应力波峰值达到传感器的时间Δt1。用同样的方法，对冲击载荷信号进行处理，得到300 Hz处冲击载荷的作用时间Δt2。这样300 Hz处应力波在结构中传播的时间就可以确定，即Δt1－Δt2，而冲击点到传感器的距离是已知的，这样该频率下各个角度的应力波在结构中的传播速度就能计算得到。根据上述方法，计算出250 Hz和300 Hz两个频率下的应力波波速，如图4(a)和图4(b)所示。同时本文也采用了另外一种方法来计算波速，即实验中接收到的信号不经过信号处理，直接用原始数据的两峰值相减作为传播时间，然后计算并拟合波速分布曲线，如图4(c)，但该方法相对与前者而言，易受冲击强度影响更容易受噪声的影响。

4.3 非破坏性冲击载荷位置识别

在获得波速分布曲线之后，用力锤在不同的位置施加冲击载荷，并记录其作用位置坐标，便于验证。对图2中所示的四个压电片传感器接收到的信号进行处理，由小波变换得到某一频率的冲击应力波在结构中传播到传感器的时间。基于这些信息，通过免疫遗传算法对式(1)定义的目标函数进行最小化实现冲击载荷位置识别。图5所示为多组冲击载荷识别结果中的一组(300 Hz波速下的识别结果，其中种群规模M=50，免疫新抗体P=20，遗传代数80)。

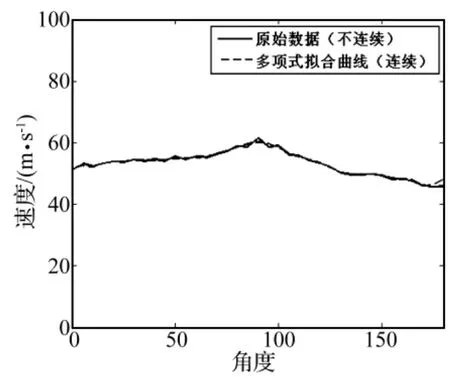
图4(a) 250Hz波速曲线Fig.4(a) The velocity curve of the stress wave(250 Hz)

图4(b) 300Hz波速曲线Fig.4(b) The velocity curve of the stress wave(300 Hz)

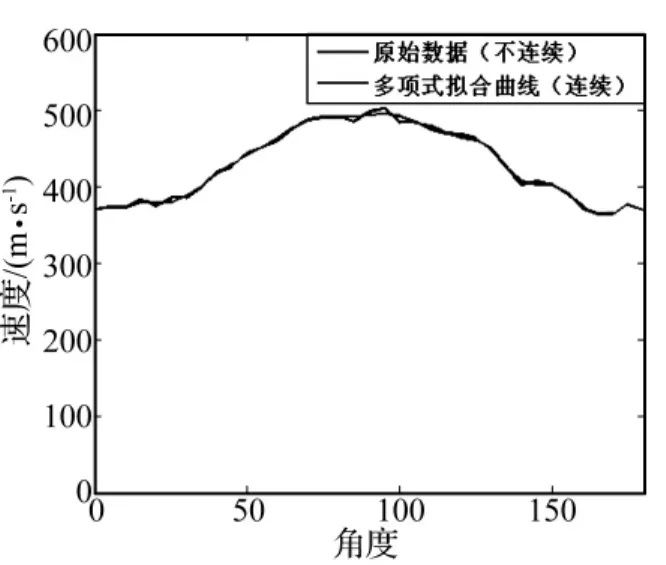
图4(c) 方法二计算得到的波速Fig.4(c) The velocity curve of other method

由图6(a)和图6(b)可以看出，识别算法在经过初期振荡后，最终能较快地收敛于真实解，从图6(c)可以看出，聚合适应度函数是逐步增大并且最后稳定在一个最大值，这保证了识别结果的最优性和收敛性。对图6(d)中的18组复合材料蜂窝夹芯结构上的冲击载荷的识别结果进行统计分析后，可以得到横坐标方向最小相对误差为0.18%，最大相对误差3.27%，平均相对误差为1.39%。纵坐标方向最小相对误差为0.40%，最大相对误差为 4.49%，平均相对误差为2.49%，总平均误差为1.78%，识别结果已经能够满足工程需要，表明了所提出冲击位置识别方法的有效性。

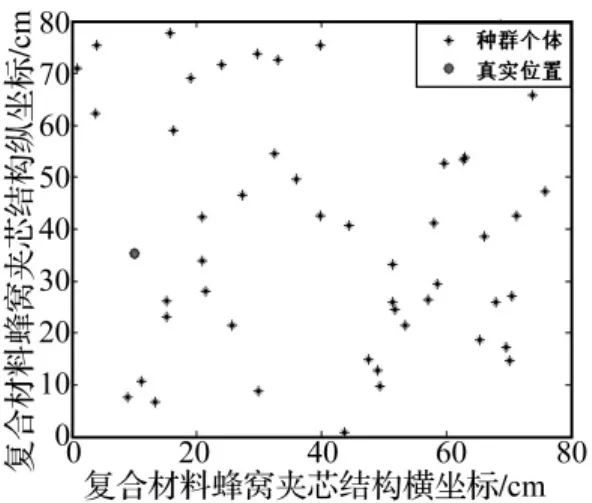
图5(a) 母代种群识别情况Fig.5(a) The identification condition of the original population

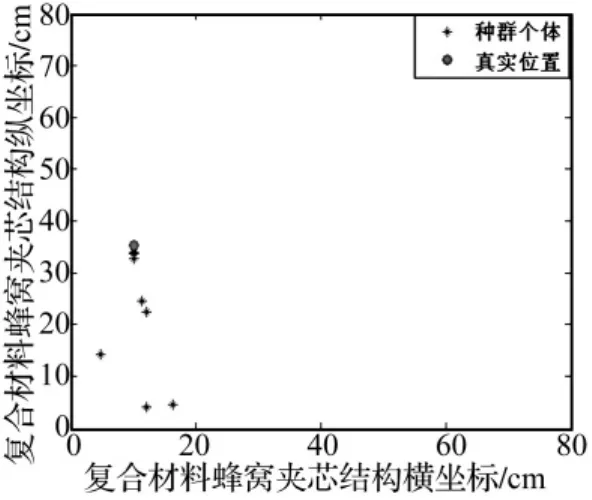
图5(b) 末代种群识别情况Fig.5(b) The identification condition of the final population

4.4 破坏性冲击载荷位置识别

在实际工程中，冲击载荷作用于结构可能造成损伤，因此具有在结构破坏时对冲击载荷位置的识别能力是判断这个识别算法是否有效和具有实际价值的重要的标准。本文对破坏性的冲击载荷位置识别也进行了实验研究。

继续在该复合材料蜂窝夹芯结构做冲击载荷实验，冲击能量为10 J，该冲击已经造成了目视的局部塌陷。

接下来对压电片传感器采集到的信号进行小波变换处理，研究其时频特性，图6是选取了其中一组信号的小波分析图。从图3(b)和图6对照中可以看出，虽然冲击能量增大，但其主要频率范围却变化很小，因此继续可以用本文的方法识别冲击载荷位置。

用不同频率的波速结合免疫遗传算法识别冲击载荷位置，结果如表1所示。

表1 冲击载荷位置实际值与识别值的比较Tab.1 Comparation of the actual location and identification

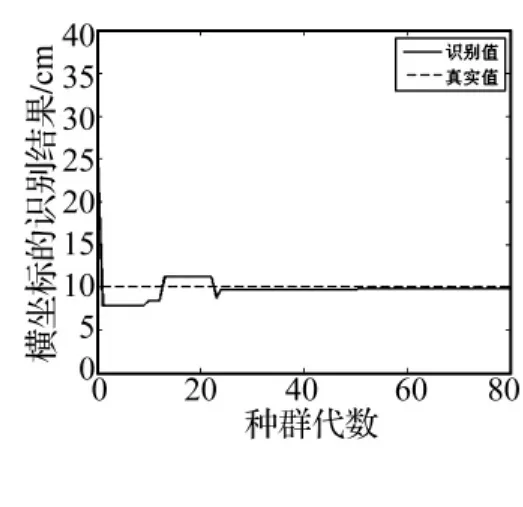
图6(a) 横坐标识别结果Fig.6(a) The identification of the horizontal coordinate

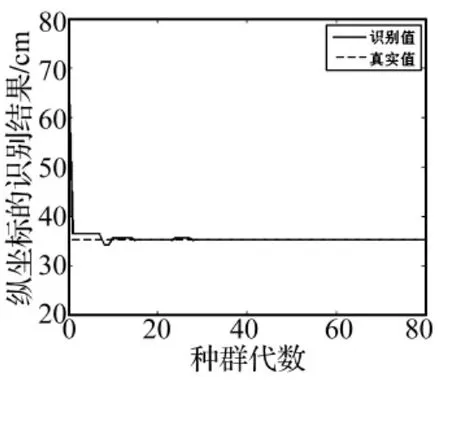
图6(b) 纵坐标识别结果Fig.6(b) The identification of the vertical coordinate

图6(c) 聚合适应度函数进化图Fig.6(c) The iteration of the polymerize fitness

图6(d) 总识别结果图Fig.6(d) The identification result

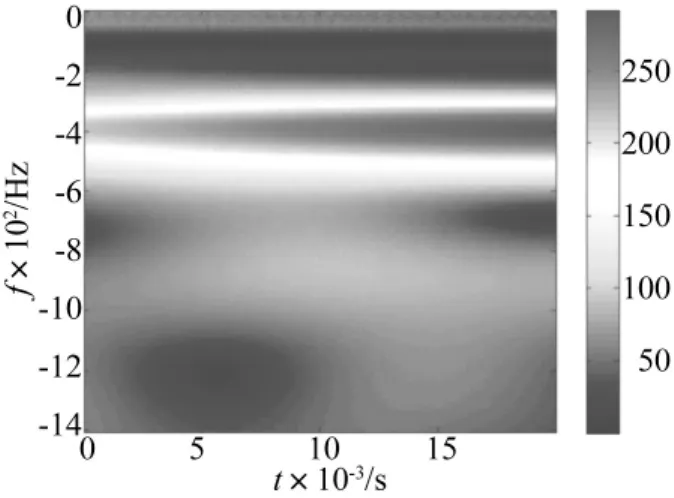
图7 破坏性冲击应力波信号小波时频图Fig.7 The wavelet transform of the damage signal

对表1冲击载荷位置的识别结果进行分析，可以得出用频率为250 Hz的应力波波速去识别冲击载荷位置，其相对误差为4.63%;用频率为300 Hz的应力波波速去识别冲击载荷位置，其相对误差为2.72%;用未经信号处理的应力波波速去识别冲击载荷位置，其相对误差为6.15%。可以看出采用小波变换方法对信号进行处理后提高了冲击位置的识别精度，并验证了所提出方法对破坏性冲击载荷位置识别的有效性。

5 结论

本文对复合材料蜂窝夹芯结构健康监测进行了研究，提出了一种基于应力波和免疫遗传算法的冲击载荷位置识别方法，并进行了实验验证。本文所做工作的主要结论有以下几点:

(1)采用Gabor小波函数处理应力波波速，能够提取信号中心频率下的波速，提高了信噪比，因此能比较准确的计算出波速并有效减少噪音的影响。

(2)采用免疫遗传算法作为载荷位置识别算法，相对于普通的遗传算法和其它迭代优化算法而言提高了识别效率和精度。

(3)本文提出的识别方法能够有效地定位复合材料蜂窝夹芯结构上的冲击载荷，因其不依赖于材料物理性质，因此在其它类似的结构上也有一定的适用性。

［1］谢宗蕻，苏 霓，张 磊，等.复合材料蜂窝夹芯板低速冲击损伤扩展特性［J］.南京航空航天大学学报，2009，41(1):31－35.

［2］张广平，戴干策.复合材料蜂窝夹芯板及其应用［J］.纤维复合材料，2000，25(2):25－29.

［3］窦长河，程小全，郦正能.复合材料蜂窝夹芯板低速冲击后压缩强度估算［J］.北京航空航天大学学报，1998，24(5):555－558.

［4］Wang C S，Chang F K.Diagnosis of impact damage in composite structures with builtin piezo electrics network［A］.Proceedings of the SPIE，Smart Structures and Materials.San Diego，CA，2000:13－19.

［5］Cawley P，Alleyne D.The use of Lamb waves for the long range inspect ion of large structures［J］.Ultrasonics，1996，34(2):287－290.

［6］Sung D U，Oh J H，Kim C G，et al.Impact monitoring of smart composite laminates using neural network and wavelet analysis［J］.Journal of Intelligent Material Systems and Structures，2000，11(3):180－190.

［7］Jones R T，Sirkis J S，Friebele E J.Detection of impact location and magnitude for isotropic plates using neural networks［J］.Journal of Intelligent Material Systems and Structures，1997，8(1):90－99.

［8］龚仁荣，顾建祖，骆 英，等.Gabor小波时频分析在声发射信号处理中的应用［J］.中国测试技术，2006，32(1):76－79.

［9］Jeong H，Jang Y S.Wavelet analysis of p late wave propagation in composite laminates ［J］. Composite Structures，2000，49(4):443－450.

［10］Kishimoto K，Inoue H，Hamada M，et al.Time frequency analysis of dispersive waves by means of wavelet transform［J］.Journal of Applied Mechanics，1995，62(4):841－846.

［11］周 明，孙树栋.遗传算法原理及应用［M］.北京:国防工业出版社，1999:11－12.

［12］严 刚，周 丽，孟伟杰.基于Lamb波与时频分析的复合材料结构损伤监测和识别［J］.南京航空航天大学学报，2007，39(3):397－402.

［13］陈 琦，马向阳.求解串并联系统配置问题的免疫遗传算法［J］.计算机工程与应用，2010，46(15):235－238.

［14］夏 虎，庄 健，王立忠，等.一种考虑环境作用的协同免疫遗传算法［J］.西安交通大学学报，2009，43(11):80－84.