近爆作用下钢筋混凝土板动态破坏的数值模拟研究
龚顺风,邓 欢,朱升波,金伟良
(浙江大学 结构工程研究所,杭州 310058)
1 数值模型
在数值模拟中,爆炸冲击波首先在如图1所示的1D楔形空气中传播,当冲击波波阵面到达距离爆心0.5 m处,即相当于接近钢筋混凝土板上表面处,将其映射到3D模型中计算其与钢筋混凝土板的相互作用。板的净尺寸为1.0 m ×2.0 m ×0.1 m,钢筋直径为8 mm,长边方向钢筋间距为100 mm,短边方向钢筋间距为120 mm,双层双向布置,如图2所示。炸药置于距板顶面中心0.5 m高度处。钢筋混凝土板的两个长边自由,短边采用简支约束,以此模拟单向板的工作状态。钢筋和混凝土均采用Lagrange网格进行建模,其中混凝土单元数为464 208,钢筋为9 872。空气采用Euler-FCT算法,边界面设为物质流出。在爆炸荷载作用下,由于作用的时间非常短,通常可以假定钢筋和混凝土之间的粘结是完好的,同时混凝土单元的大变形会导致网格的扭曲,为解决网格的大变形问题,模型中采用侵蚀算法(Erosion)处理,这种算法将失效的混凝土单元自动删除,避免了网格扭曲造成的计算精度下降、计算步长变小等问题。

图1 TNT与空气的一维楔形模型Fig.1 Geometry of 1D wedge with axial symmetry

图2 钢筋布置Fig.2 Rebar arrangement
2 材料模型
2.1 空气和炸药的状态方程
通常将空气假定为理想气体,采用线性多项式状态方程来描述爆炸后空气的性能。根据Gama准则,空气的状态方程可表示为[9-10]:

式中:pa为气体压力;γ为比热比,理想气体取值为1.4;初始时刻的空气密度ρa=1.29 kg/m3;E为空气单位体积的内能,其初始值E0=2.5×105J/m3。对于不同炸药爆炸的数值模拟,一般采用经验的JWL状态方程来描述炸药爆轰过程压力和内能及相对体积的关系[9,10]:
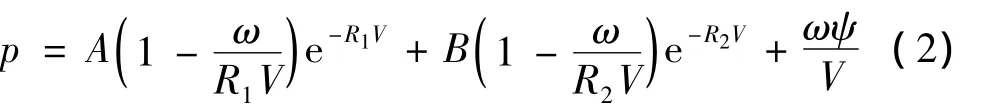
式中:p为爆炸产生的压力,V为单位体积装药产生的爆轰产物的体积,即当压力为p时的体积与初始体积的比值,ψ是炸药的比内能;A、B、R1、R2和ω是由相关爆炸实验确定的材料参数。对于TNT炸药,初始密度ρ0=1 630 kg/m3,单位体积的初始内能 ψ0=6.0 ×103MJ/m3,其他相关参数见表1。

表1 炸药的材料参数Tab.1 Material parameters of explosive
2.2 钢筋
钢筋采用J-C模型[11],该模型适合模拟材料在大应变、高应变率和高温情况下的力学性能。在爆炸荷载作用下,热传导的时间远大于爆轰持续的时间,且由于变形热导致的温升并不大,材料出现强化继而接近失效时,应力减小的幅度比较有限,所以温度软化效应并不明显。爆炸冲击荷载作用下混凝土结构中钢筋的应变率可以达到 50 s-1~100 s-1[11-12],图 5 给出钢筋在不同应变率下的应力应变关系曲线,该材料本构模型可表示为:
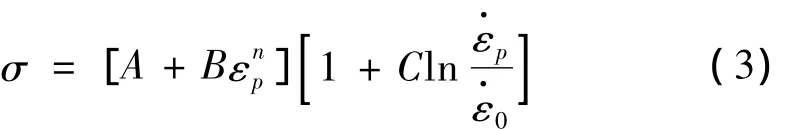
式中:εp为等效塑性应变为等效塑性应变率为参考塑性应变率,取=1.0 s-1。A表示材料的屈服强度是对材料强化段的描述,C为应变率敏感参数。钢筋的失效应变取为0.1,其他相关参数见表2。
测试关注网络参数N,节点参数Rs,Rc,以及覆盖百分比p对无线传感器生命期的影响,即关注在上述参数取值不同的情况下,节点所求得的覆盖集情况以及算法的性能表现。

表2 钢筋的材料参数Tab.2 Material parameters of reinforcing bar
2.3 混凝土
混凝土采用AUTODYN软件材料库中的CONC-35 MPA材料模型,该模型包括P-α状态方程,RHT[12]强度模型和损伤模型以及侵蚀算法。RHT强度模型通过引进三个不同的强度面可以较好地表示混凝土材料具有屈服强度、最大强度及残余强度的特性,能较为合理地描述混凝土从弹性到失效的整个过程,是当前比较适合用来模拟混凝土材料在爆炸冲击荷载作用下动力特性的模型。
2.3.1 三个强度面
最大强度面定义为静水压力、偏应力面上罗德角和应变率的函数,可表示为:
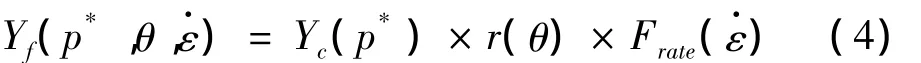
其中,受压子午线为:
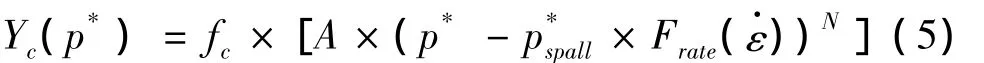


式中:ψ=rt/rc,rt为静水压力轴到拉伸子午线的距离,rc为静水压力轴到受压子午线的距离,罗德角θ是第二和第三偏应力不变量的函数,可以由下式计算得到:
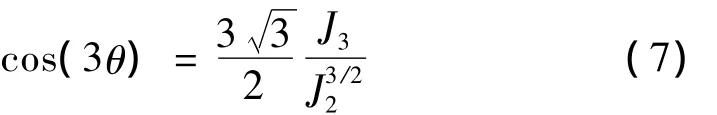
在RHT模型里,引入屈服面主要考虑材料应变的硬化效应,将最大强度面缩放一定比例来得到:
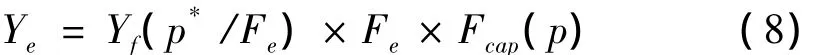
式中:比例系数Fe为屈服强度和最大强度的比值,是静水压力的线性函数;Fcap(p)为弹性极限的帽子函数,用于限制静水压力作用下的弹性偏应力。
为了描述压碎后混凝土材料的剩余强度,RHT模型单独引入了残余强度面,为压力的指数函数,其定义为:

式中:Yr为残余强度,B、M为残余强度面参数,缺省值分别为1.6 和 0.61。
图6为相应的三个强度面示意图,对于在屈服强度面和最大强度面、最大强度面和残余强度面之间的加载面,可以通过相互间的线性插值得到。

图3 有限元数值模型Fig.3 Cross-section view of numerical model

图4 冲击波图Fig.4 Pressure contours

图5 不同应变率下钢筋的应力应变关系Fig.5 Constitutive model of rebar at different strain rate

图6 最大强度、屈服强度和残余强度面Fig.6 Maximum strength,yield strength and residual strength surfaces
2.3.2 损伤定义及侵蚀算法
RHT模型认为损伤是塑性应变的累积,损伤变量D定义为:

式中:Δεp为等效塑性应变增量,Δμp为塑性体积应变增量,D1、D2为损伤参数。损伤度D随塑性应变的累积而增长。材料完全失效后,损伤变量D=1.0,材料只能承受有限压力,不能承受任何拉应力。
混凝土材料的应变率敏感性是引起动荷载作用下混凝土材料力学性能显著区别于其准静态荷载作用下的主要因素。混凝土在准静态荷载作用下的峰值拉应变为0.000 2(为峰值压应变的1/10),考虑到软化阶段,混凝土完全失效时的应变可认为是0.000 6。而在爆炸荷载作用下,混凝土的应变率为10 s-1~100 s-1,相应的强度动力放大因子可达到5.0甚至更大,但是断裂应变的增强比强度的放大要小,故混凝土的失效拉应变取为0.001。
2.3.3 采用修正后参数对应力软化特性的影响
文献[13]对几种广泛使用的混凝土材料模型进行了全面的分析评价,并指出应用于AUTODYN软件中的RHT模型缺省参数存在较大的问题。为了得到材料软化的实际特性,对参数B、M、D1、D2和最小失效拉应变εminf进行修正。对于残余强度面的可调参数B和M建议取值0.7和0.8,εminf取0.000 8代替原来的缺省值 0.01,系数D1推荐取值 0.015,D2=1.0 保持不变。混凝土的密度ρ=2.55×103kg/m3,抗压强度为35.0 MPa,抗拉强度取为 3.5 MPa,剪切模量G为1.67 ×104MPa。
为了验证RHT模型的实际特性,进行了数值模拟试验用以评价该材料模型在不同荷载作用下的应力-应变关系。数值试验采用单元体法,荷载由具有一定速率的位移控制,作用于节点上,施加必要的约束以限制刚体运动,如图7所示。数值试验显示使用缺省参数时,RHT模型表现出在拉压作用下应变软化范围出现不合实际的递减过程,如图8(a)所示的单轴拉伸试验,完全破坏状态下应变的数量级为0.01,远远大于一般物理实验实际观察的拉伸破坏应变,同样的单轴受压问题可见图8(b)。采用修正后的参数,混凝土材料能得到比缺省参数较为合理的力学性状。

图7 RHT模型的单轴试验模型Fig.7 Typical model setup of a uniaxial compression test
3 数值模拟
3.1 爆炸荷载
炸药在空气中爆炸,是一个能量高速释放的过程,高温高压的爆炸产物高速膨胀,强烈压缩周围空气,形成压力很高的空气冲击波。当爆炸面产生的压应力波传播到介质与空气的分界面时,冲击波将发生反射,反射压力通常为入射超压的2~8倍。1969年,美国军方出版的TM5-1300[14]结构抗爆作用规范给出的大范围内爆炸荷载参数已被先前诸多应用所验证,如图9所示,为各比例距离峰值超压的变化情况,其中Pso为TNT炸药在自由空气中爆炸时的冲击波峰值超压,Pr为反射冲击波的峰值超压。计算所得的钢筋混凝土板面中心的压力时程曲线如图10所示,爆炸压力在开始阶段迅速达到峰值,并随时间推移在1 ms内超压降低为0。反射波的峰值超压比TM5-1300值在自由空气中测得的要大,但与TM5-1300反射超压相比则要小,主要是因为数值模拟中钢筋混凝土板的刚度与实际测量中的刚性体有一定偏差。
3.2 钢筋混凝土板动力响应与破坏模式分析
在爆炸作用下板跨中最大挠度是衡量其破坏程度的一个重要指标。由图11和图12可知,最大速度出现在爆炸冲击波结束时,而后结构由于惯性作用将继续向下运动,另外,随着炸药量的增加,板跨中的挠度随之增大。当炸药量为1 kg时,板在20 ms时停止运动,最终位移为17 mm。当炸药量为2 kg时,板的竖向位移为61 mm。5 kg TNT炸药作用下,板跨中在0.77 ms达到最大速度 16.7 m/s,随后速度迅速衰减,在20 ms时位移为143 mm。
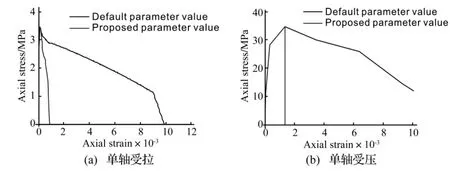
图8 默认参数与新参数的RHT模型应力应变曲线比较Fig.8 Comparison of stress-strain curves generated by RHT model with default and newly proposed model parameter values

图9 TNT球形装药海平面处爆炸荷载参数Fig.9 Pressure and reflected pressure for a spherical TNT detonation at sea level

图10 钢筋混凝土板面处的反射压力时程曲线Fig.10 Reflected pressure on the surface of the RC slab
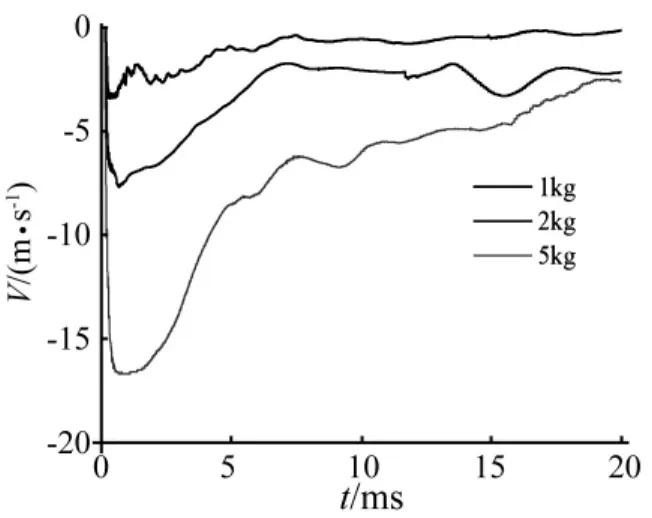
图11 不同炸药量下板中心点竖向速度时程曲线Fig.11 Vertical velocity of middle point in slab under different blast loadings
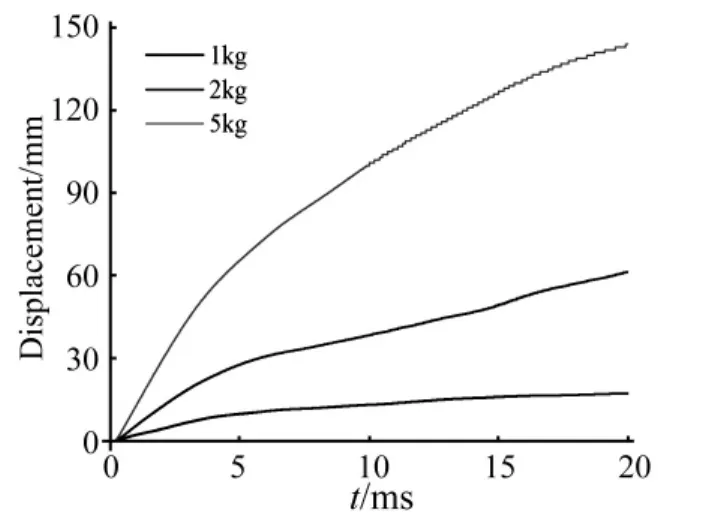
图12 不同炸药量下板中心点竖向位移时程曲线Fig.12 Vertical displacement of middle point in slab under different blast loadings
钢筋混凝土板在不同炸药量作用下的破坏模式如图13所示。由图可知,在不同的爆炸荷载作用下,压缩应力波均在板的迎爆面产生损伤,并传播至板的背爆面形成强拉伸波,造成背爆面混凝土的层裂和崩塌。随着炸药量的增大,钢筋混凝土板的破坏越严重,并表现出不同的破坏模式。在1 kg TNT炸药作用时,板正面纵向中部有一条宽度为100 mm左右的混凝土压碎带,背面纵向中部有一条宽度约5 mm的受拉破坏裂缝,板主要发生弯曲破坏;当炸药量为2 kg时,混凝土板受拉区破坏较为严重,板背面纵向中部出现多条受拉破坏的裂缝,表现出明显的双向弯曲。在5 kg TNT炸药作用时,钢筋混凝土板破坏严重,板整体表现为弯曲破坏,中部横向裂缝增多,混凝土板被分割成许多块体,部分钢筋屈服但没发生断裂;当炸药量为10 kg时,板的破坏主要集中在中央,呈现弯曲冲切耦合破坏,板中央部分纵向受拉钢筋发生断裂,在迎爆面与背爆面之间的板中心区域发生上下贯通破坏,形成了一个直径大于1.0 m的爆坑,有混凝土碎块飞出。

Fig.13 不同炸药量作用下钢筋混凝土板的损伤Fig.13 Damage distribution of RC slab under different explosive charge

图14 2kg Comp B炸药作用下钢筋混凝土板的损伤Fig.14 Damage distribution of RC slab in 2 kg Comp B charge case
3.3 数值模拟与试验结果的比较
选用文献[15]钢筋混凝土板试件进行建模,板的净尺寸为1.3 m ×1.0 m ×0.12 m,钢筋直径10 mm,纵向受力钢筋间距为100 mm,分布钢筋间距为120 mm,双层双向布置。2 kg Comp B炸药置于距板顶面中心0.6 m高度处。在爆炸荷载作用下,压缩应力波在板的迎爆面产生损伤,并传播至板的背爆面形成强拉伸波,造成背爆面混凝土的剥落和层裂,破坏过程如图14所示。钢筋混凝土板背面纵向中部较横向中部先出现受拉破坏裂缝,在2 ms时,横向裂缝发展,最终宽度约为5 mm,板发生明显的双向弯曲破坏。在板中心区域,出现环形裂缝,具有双向弯曲的角部裂缝特征。钢筋混凝土板受拉区破坏严重,板背面中部出现多条横向受拉破坏的裂缝,板正面和背面的破坏特征与试验得到的图15和图16[15]吻合较好。

图15 正面混凝土压缩裂缝Fig.15 Compression crack of RC slab upper surface

图16 背面的受拉破坏Fig.16 Tensile damage of RC slab back surface
4 结论
本文采用AUTODYN软件建立了炸药、空气和钢筋混凝土板的三维数值模型,考虑了应变率对钢筋和混凝土材料动力本构特性的影响以及炸药-空气-结构之间的流固耦合相互作用,分析了不同炸药量作用下钢筋混凝土板的损伤机理和破坏特征,结果表明:
(1)钢筋混凝土板面承受的爆炸荷载与自由场冲击波大小和板的刚度密切相关。入射超压越大,则反射越强,升压时间短,衰减迅速。
(2)建立的流固耦合数值模拟方法可以合理地展现钢筋混凝土板从混凝土开裂、碎片形成、部分钢筋屈服断裂到板局部震塌的动态演变过程。
(3)随着炸药量的加大,钢筋混凝土板的破坏逐渐由整体弯曲破坏转变为局部的冲切破坏。
[1]Gong S F,Lu Y,Jin W L.Simulation of air blast load and its effect on RC structures[J].Transactions of Tianjin University,2006,12(suppl):165-170.
[2]Yuan L,Gong S F,Jin W L.Spallation mechanism of RC slabs under contact detonation[J].Transaction of Tianjin University,2008,14(6):464-469.
[3]龚顺风,金伟良,何 勇.内部爆炸荷载作用下钢筋混凝土板的动力响应研究[J].振动工程学报,2008,21(5):516-520.
[4]阎 石,张 亮,王 丹.钢筋混凝土板在爆炸荷载作用下的破坏模式分析[J].沈阳建筑大学学报,2005,21(3):177-180.
[5]张 舵,卢芳云,王瑞峰.钢筋混凝土板在爆炸作用下的破坏研究[J].弹道学报,2008,20(2):13-16.
[6] Gong S F,Lu Y,Tu Z G,et al.Validation study on numerical simulation of RC response to close-in blast with a fully coupled model[J]. StructuralEngineering and Mechanics,2009,32(2):283 -300.
[7] Zhou X Q,Kuznetsov V A,Hao H,et al.Numerical prediction of concrete slab response to blast loading[J].International Journal of Impact Engineering,2008,35(10):1186-1200.
[8]Xu K,Lu Y.Numerical simulation study of spallation in reinforced concrete plates subjected to blast loading[J].Computers& Structures,2005,84(6):431-438.
[9] AUTODYN theory manual,revision 6.1 [M].California:Century Dynamics,San Ramon,2006.
[10] AUTODYN User Manual,Revision 6.1 [M].California:Century Dynamics,San Ramon,2006.
[11]Johnson G R,Cook W H.A constitutive model and data for metals subjected to large strains,high strain rates and high temperatures[C].Proceedings of the seventh international symposium on Ballistics.Hague:1983,541-547.
[12] Riedel W,Thoma K,Hiermaier S,et al.Penetration of reinforced concrete by BETA-B-500 numerical analysis using a new macroscopic concrete model for hydrocodes[C].Proceeding of the Ninth International Symposium on Interaction of the Effects of Munitions with Structures,1999,315-322.
[13]Tu Z G,Lu Y.Evaluation of typical concrete material models used in hydrocodes for high dynamic response simulations[J].International Journal of Impact Engineering,2009,36(1):132-146.
[14] TM5-1300.Structures to resist the effects of accidental Explosions[S].US Army,USA,1990.
[15]孙文彬.钢筋混凝土对边简支板的爆炸试验[J].力学与实践,2008,30(4):58-60.

