上海世博文化中心TMD减轻人致振动分析与实测研究
吕西林,丁 鲲,施卫星,翁大根
(同济大学 土木工程防灾国家重点实验室,上海 200092)
人致振动问题主要包括人行荷载模式和舒适度评价标准两方面。人在行走过程中引起的动力荷载是相当复杂的,其产生的力可以分为竖向、横向及纵向三个方向。步频的统计分布对确定步行荷载的卓越频率以及人群荷载的数值仿真都十分重要。各国学者的研究揭示了人在不同活动状态下的典型频率范围:步行1.6 Hz~2.4 Hz,跑步 2.0 Hz~3.5 Hz,跳跃 1.8 Hz~3.4 Hz,弹跳 1.5 Hz~3.0 Hz,身体水平晃动 0.4 Hz~0.7 Hz。人在不同的活动状态下产生的三个方向的力均可以用傅立叶级数的形式表示,由于其概念明确、使用方便,被很多规范和标准采用,实际应用时最多考虑前5阶谐波分量[1-2]。
在研究人体振动舒适度的过程中,由于加速度易于测量,人们常常使用它作为振动舒适度指标,实践中采用的加速度指标有峰值加速度、均方根加速度、振动剂量等形式。各国规范、标准采用的指标也不尽相同。人体振动舒适度评价是一个非常复杂的问题,不同的人对同一振动的反应不同,同一个人在不同环境下对相同的振动反应也不同,尽管各国学者在此方面已进行了大量的研究,但是始终难以得到一致的、确定的结论[2-7]。
上海世博文化中心六层为悬挑钢结构楼盖,计算表明结构的竖向振动频率非常密集且覆盖了人正常行走的频率范围,在世博会举行期间大量人流的涌入可能会导致舒适度问题。本文对采用调谐质量阻尼器(Tuned Mass Damper)进行人致振动控制的上海世博文化中心进行了大量计算分析和现场实测,结果表明在一定情况下TMD能有效减小结构竖向振动响应。
1 工程概况
上海世博文化中心是2010年上海世博会永久性场馆之一,位于世博园核心区滨江带。建筑主体为18 000座多功能场馆及环绕主场馆周边的六层建筑,总建筑面积约140 277 m2。建筑形态似空中飞碟,平面投影呈三角形,平面尺寸为165 m×205 m,主场馆布置呈椭圆形。
主体结构沿环向由36榀悬臂长度不一的钢桁架及内框架组成,地上六层,地下二层,屋面最高处距离室外地面41.5 m。内框架围绕18 000座主场馆布置,框架间距11.5 m,框架柱采用矩形钢管混凝土。沿径向利用碟形主体的高度布置大跨悬臂钢桁架,桁架根部高度12 m,悬臂长度20 m~31 m不等。利用电梯分别在东南角增加两个、西南角增加三个剪力墙芯筒,悬臂桁架铰接搁置在芯筒角点上,并在芯筒上的桁架间设置转换桁架,使芯筒中间轴线上悬臂桁架的长度均控制在31 m以内。内框架通过环向框架梁将各榀框架联系在一起,以抵抗水平地震作用和水平风荷载。内框架既承担着悬臂桁架传来的竖向荷载和弯矩,又承担着整个结构的水平作用,是整个结构的主要抗侧力构件。六层结构平面如图1所示。
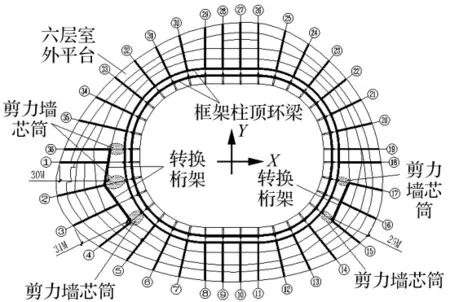
图1 六层结构平面示意图Fig.1 Structural plan of 6thfloor
2 计算分析
2.1 结构模态分析
本文采用两种有限元软件Midas和Sap 2000分别计算结构的动力特性,其有限元模型分别如图2、图3所示。表1为Midas和Sap2000模型计算的前10阶固有频率对比,第一阶振型为整体扭转,第二阶振型为XZ平面摆动,第三阶振型为YZ平面摆动,高阶振型除少数为局部振动外,其余均为竖向振动。从表中可以看出,结构的高阶固有频率较低,其频谱覆盖了行人的整个步行频率范围(1.6 Hz~2.4 Hz),特别是在步行频率的中心位置2 Hz附近较为密集,因此根据分析结果,结构很有可能发生共振现象。
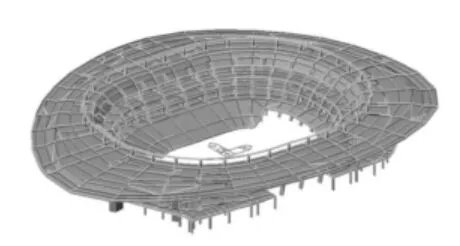
图2 Midas计算模型Fig.2 Midas computation model

图3 Sap 2000计算模型Fig.3 Sap2000 computation model

表1 世博文化中心结构前10阶频率Tab.1 First ten frequencies of structure
2.2 各榀桁架梁频域分析
由于在人的步行激励中一阶谐波占主要成分,因此在简化计算时可忽略二阶以上谐波,则步行荷载对楼板的作用可近似表示为一间谐荷载。针对各榀悬臂钢桁架,分别在稳态载荷作用点施加不同频率的简谐激励,然后分析输出参考点的竖向加速度以计算频率响应。荷载作用点和输出参考点位置见图4。表2列出了其中几榀桁架梁的竖向共振频率。
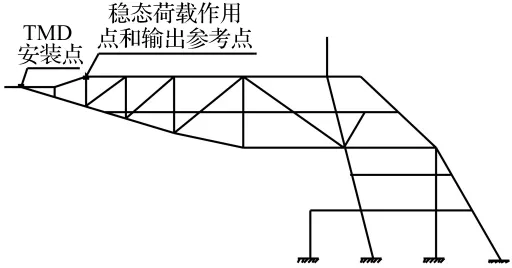
图4 荷载作用点和输出参考点位置(1轴)Fig.4 Position of steady-state load and output
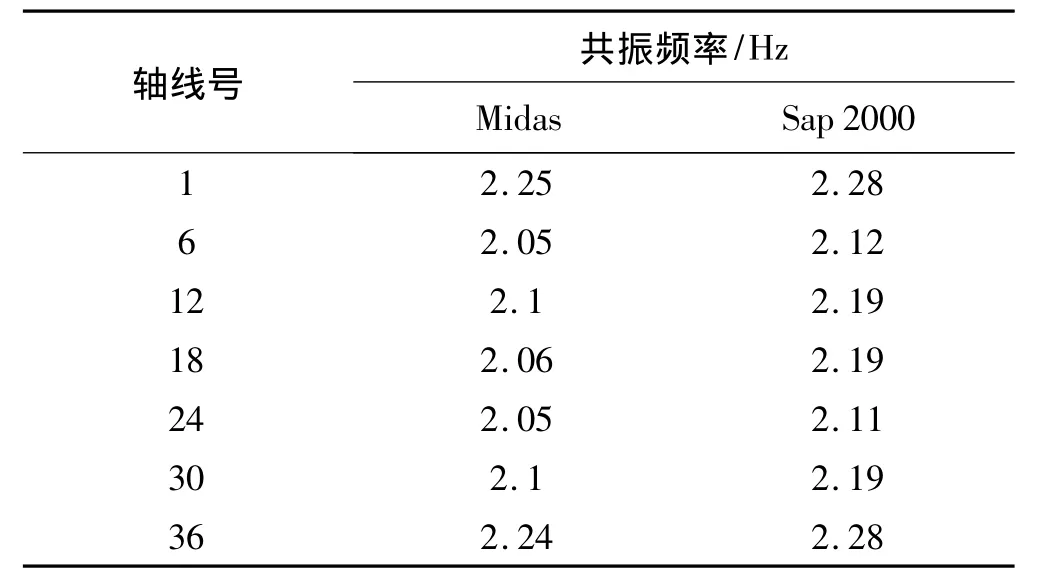
表2 桁架梁竖向共振频率Tab.2 Vertical resonance frequency of truss
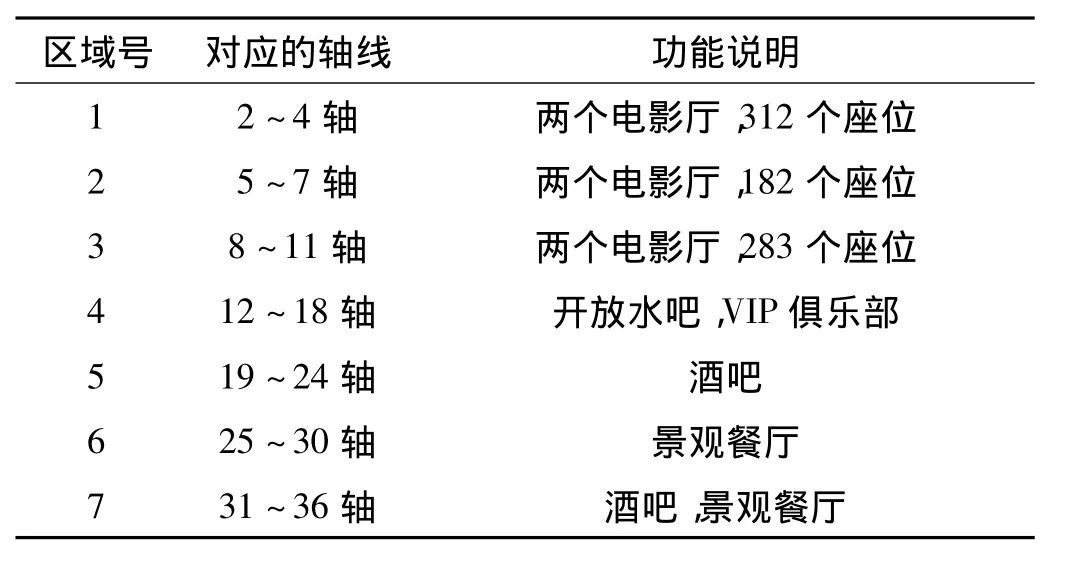
表3 各区的位置与功能Tab.3 Position and function of different zone
另外,按照建筑功能的不同将1~36轴分成7个连续区域(各区域位置和功能见表3),每个区域包含若干轴线,以每个区域为单位进行谐波响应分析。在区域包含各轴线的节点上施加简谐荷载(如图5所示),分析参考点的竖向加速度得出各功能区的竖向共振频率,如表4所示。
从中可以看出,不管是对单轴桁架还是对某几轴桁架组成的连续区域进行频域分析的结果均表明悬臂钢桁架梁的竖向振动频率在2.0 Hz-2.2 Hz左右,均有可能引起人体舒适度问题。

图5 区域1激励荷载示意图Fig.5 Steady-state load in zone 1

表4 各功能区竖向共振频率Tab.4 Vertical resonance frequency of each zone
2.3 TMD减振计算分析
2.3.1 荷载模式和舒适度标准
计算采用的人行激励时程曲线为国际桥梁与结构工程协会(IABSE)所给定的连续步行荷载模式,其中假设单人重量700 N,加载频率根据不同区域的共振频率而调整[8]。图6所示为步行频率为2.0 Hz时的IABSE时程曲线。
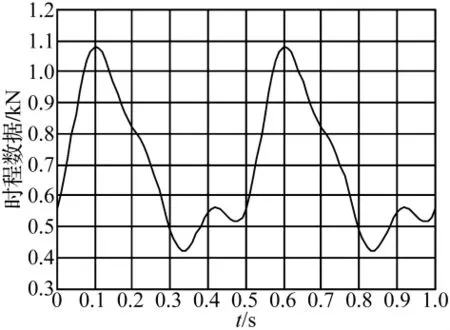
图6 步频为2.0 Hz的时程激励曲线(IABSE)Fig.6 Walking time history curve in frequency 2.0 Hz(IABSE)
目前,我国在建筑振动测试方面有《住宅建筑室内振动限值及其测量方法标准》(GB/T 50355-2005)的规定,但是其采用分贝为计量单位。另外《城市人行天桥与人行地道技术规范》(CJJ69-95)中的相关条文:“为避免共振,减少行人不安全感,天桥上部结构竖向自振频率不应小于3Hz”,但对于商业建筑无相关规定,而国际标准化组织ISO和部分欧美国家都颁布并实施了人体舒适度标准及规范。本文根据美国AISC颁布的设计指南《Floor Vibrations Due to Human Activity》[9]中的规定,以 5 gal作为第一控制指标,15 gal作为第二控制指标,具体见表5所示。

表5 民用建筑楼盖振动加速度限制Tab.5 Acceleration limits of civil structure floor
2.3.2 减振方案
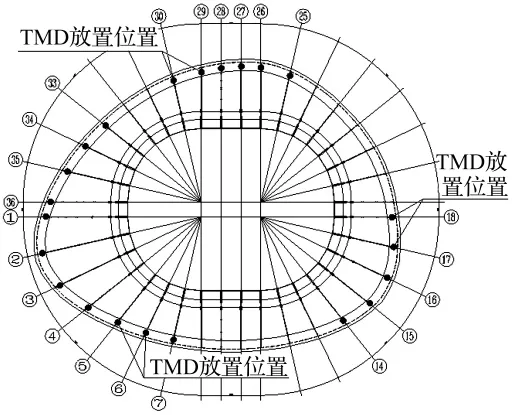
图7 240 t TMD安装位置示意图Fig.7 Installation site of 240 tons TMD
最初考虑采取240 tTMD的布置方案,在1轴~7轴、14轴~18轴、25轴~30轴、33轴~36轴一共22个轴布置了50个TMD。产品由隔而固(青岛)振动控制有限公司提供,单个TMD参数如下:质量4.8 t,固有频率2.15 Hz,阻尼比0.08。其中1轴-3轴各安装4个TMD,总重为19.2 t,其它19根梁上的各安装2个,总重为9.6 t。图7为 TMD在整个场馆的安装位置示意图。
2.3.3 减振效果分析
计算时分7个功能区分别计算,步行激励以面荷载形式施加在楼面上。设各区的人员密度约为0.74人/m2(大致等于电影厅中座位的密度),同步比例20%,步行激励时程采用IABSE曲线。设各区同步行走人员的步行频率为相应各区的固有振动频率(表4中计算结果),计算连续踏步40次。
为了考虑到可能出现的不利情况,对荷载的作用面积进行了适当扩展。如以1区为例,1区所指的区域为2轴~4轴,但在进行荷载假定时认为面荷载作用在1轴~5轴的整个区域,同时还认为外侧观光平台也有步行激励作用。采用了Midas和Sap 2000软件进行了分析,限于篇幅,仅列出了Midas的部分计算结果。图8-图10为其中几轴安装TMD前后的竖向加速度时程曲线对比。
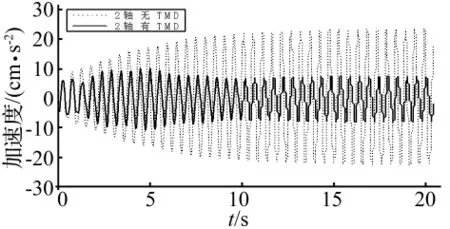
图8 2轴竖向加速度时程曲线对比Fig.8 Acceleration time history curve of axis 2
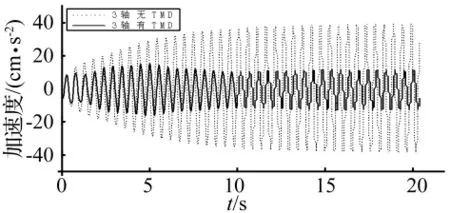
图9 3轴竖向加速度时程曲线对比Fig.9 Acceleration time history curve of axis 3

图10 30轴竖向加速度时程曲线对比Fig.10 Acceleration time history curve of axis 30
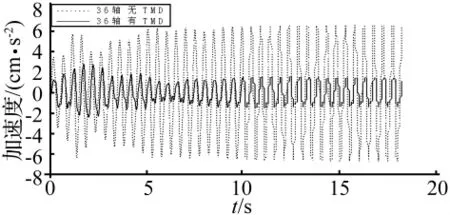
图11 36轴竖向加速度时程曲线对比Fig.11 Acceleration time history curve of axis 36
对所有36轴的分析结果表明,安装TMD后1区和6区的减震效率较高,达50%以上,而其他各区减震效率在20%-40%之间。安装TMD后部分轴线的峰值加速度从大于5 gal降到5 gal以下,仅有2、3、26、27 轴的振动超过5 gal,仅3轴峰值加速度略大于15 gal。表6列出了安装TMD前后部分轴竖向加速度峰值的变化。

表6 部分轴竖向加速度峰值及TMD的减振效率(Midas计算)Tab.6 Peak acceleration and TMD reduction effectiveness
但是,考虑到计算结果和实测结果可能有一定差距,因此先安装减震效果较好的1轴~3轴、25轴~30轴共115.2 t TMD,其他轴线TMD根据测试结果再决定是否安装。
3 现场实测
3.1 施工阶段实测结构频率
在结构楼板浇筑结束,但是面层、装修等荷载未施加的状态下对结构各榀桁架的竖向自振频率进行了测试,以便和理论计算结果进行对比。此时结构的外观如图12所示。采用加速度传感器对36榀桁架进行了脉动下的振动测试,测点布置在各桁架梁的最外端。同时按照实际状态对原有计算模型进行调整,使其符合目前状态下的结构,计算结构各榀桁架梁的竖向振动频率,对比测试和分析结果,如图13所示。从图中可以看出,现场实测各榀桁架的竖向振动频率在3.0 Hz~5.2 Hz之间,已超出人正常行走的频率范围,而且与理论计算值有一定的出入,但是此时大量荷载未施加到楼面上,测试结果与最终结果会有一定误差,因此在结构完全竣工后又对结构频率和TMD的特性进行了测试。

图12 施工阶段结构外观Fig.12 Structure under construction
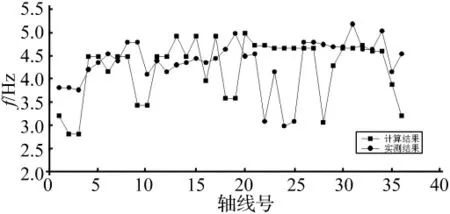
图13 计算结果和现场实测结果对比Fig.13 Comparison of computational and test results
3.2 结构竣工后现场测试
在结构竣工后进行内部装修时,对各榀桁架又进行了竖向振动频率测试,测试结果表明各榀桁架的振动频率在2.9 Hz~4.4 Hz之间,大部分大于3 Hz,与施工状态测试的结构频率相比,有增有减,整体变化不大。但是测试结果远远高于最初模型的计算结果,且结构的频率已超出了人正常行走的频率范围,发生振动引起舒适度问题的几率大大减小。
已安装的TMD频率为按照计算结果进行设计制造,所有TMD设计频率为2.15 Hz。根据测试得到的桁架梁竖向振动频率,在TMD和楼板之间增加弹簧以增大TMD自振频率使其和桁架竖向振动频率一致,这样TMD才有可能起到减振作用。
调试TMD后在各榀钢桁架端部和中部以及TMD质量块上布置加速度传感器,测试在人跑步和跳跃激励下的加速度反应,并进行频谱分析,得到TMD的自振特性,据此判断TMD的工作状况。图14为1轴测点布置图,图15为TMD实际布置图。

图14 测点布置位置图Fig.14 Layout of the acceleration transducers

图15 TMD实际布置图Fig.15 TMDs in structure
测试结果表明,绝大部分TMD工作良好,增加弹簧后TMD的振动频率为2.83 Hz~2.93 Hz,与桁架梁振动频率基本保持一致,阻尼比为3% ~6%,TMD上的振动加速度较大,说明TMD吸收部分能量,起到一定的减振作用。
另外在3轴入口处放置了3个加速度传感器测量振动响应,测点布置如图16所示。考虑了两种工况:11个人在入口周围沿箭头方向走动模拟观众出入场;4人在外走廊上连续跳跃。测试结果表明,不管TMD处于开启状态还是关闭状态,在多人行走和跳跃荷载作用下,结构的竖向振动加速度均较小,峰值均不超过6 gal。在多人行走激励下的入口处最大振动加速度级均小于60 dB,TMD对其影响不大;在外走廊行人跳跃激励下的最大振动加速度级在TMD关闭状态下为71 dB,在TMD开启的状态下为68.8 dB,TMD 有一定的减振效果。
根据测试结果,人正常行走时楼面振动较小,TMD作用有限,因此仅安装1轴~3轴、25轴~30轴TMD,其他轴桁架不安装TMD。

图16 3轴入口处测点布置图Fig.16 Layout of sensors in the entrance of axis 3
4 修正模型计算分析
通过几次的现场测试发现结构的实测频率和模型计算频率有较大误差。分析其原因可能有以下几点:
(1)模型计算结果为结构整体频率,而实测时为结构局部频率,二者有一定差异;
(2)模型计算时活荷载为满布情况,但是现场实测时实际活荷载远未达到满布状态;
(3)现场实测采用脉动法,测试结果偏大,且非结构构件和现场人员活动对测试结果有较大影响。
考虑到以上因素,本次分析对结构初始模型进行了修正,使结构计算频率与实测频率相接近,具体进行了以下修正:
(1)将所有铰接梁改为刚接;
(2)将各层活荷载进行折减,使其符合实际情况;
(3)取消考虑长期荷载作用下六层混凝土楼板的刚度折减,并考虑六层部分楼面钢肋板的作用。
采用Sap 2000对修正后的结构模型重新进行计算,初始模型和修正模型前10阶固有频率对比如表7所示。修正后结构的高阶竖向振动频率和实测结果比较接近,分析结果可靠性增大。
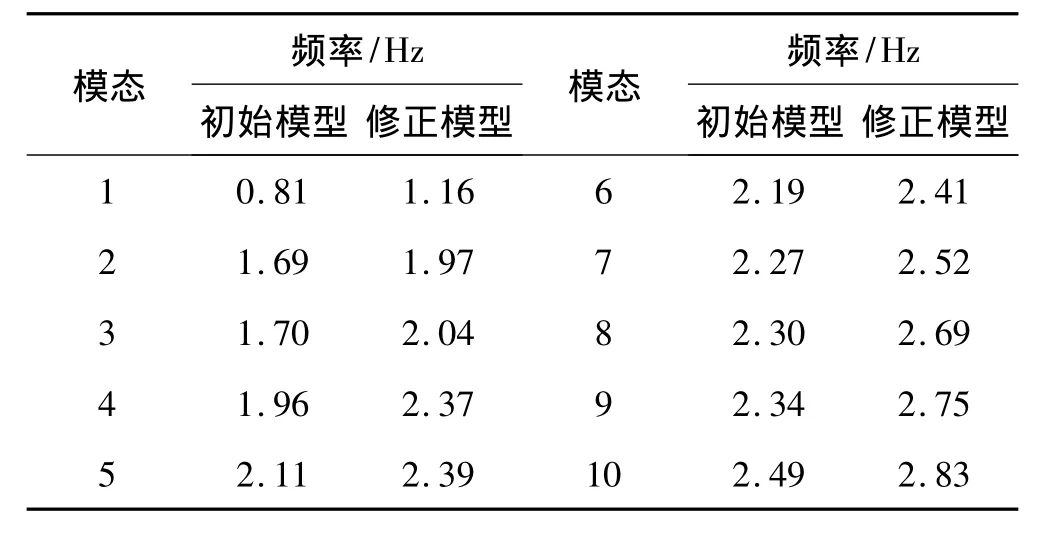
表7 初始模型和修正模型前10阶频率对比Tab.7 First ten frequencies comparison of initial model and amendment model
模型修正后,对安装TMD的1轴~3轴、25轴~30轴九榀桁架进行单轴和区域频域分析,结果表明各轴在3.0 Hz附近均有多个竖向共振频率,1轴~3轴区域的共振频率集中在2.86 Hz和2.7 Hz,而25轴~30轴区域的共振频率集中在2.52 Hz和3.14 Hz。
根据频域分析结果,结构的竖向振动频率已经超过人正常行走的频率范围,但是处于人跑动的频率范围。因此针对1轴~3轴、25轴~30轴两个区域分别计算两种不同工况,一种工况是按照人正常行走频率为2.0 Hz进行计算,另一种是考虑人快速走动或奔跑时情况,按照结构竖向共振频率进行计算,选取与测试结果接近的振动频率,即1轴~3 轴为 2.86 Hz,25 轴 ~30轴为 2.52 Hz。分析的荷载模式与前述相同,采用IABSE时程曲线。

图17 人正常行走时TMD减震效果Fig.17 TMD reduction effectiveness in normal walking condition

图18 人奔跑状态下TMD减震效果Fig.18 TMD reduction effectiveness in run condition
分析结果表明,当人以2.0 Hz的频率正常行走时,装与不装TMD的各轴竖向振动加速度时程曲线基本重叠,TMD对其影响较小。同时也注意到人行荷载作用下,各参考点的振动较小,加速度峰值处于3gal~8gal的范围内,基本满足AISC设计指南。而当人以结构竖向共振频率快速走动或奔跑时,未装TMD的竖向振动呈较明显共振效应,安装TMD后,共振现象明显减弱,各轴竖向加速度峰值也有一定程度的减小,均控制在15 gal以内,TMD的平均减振效率约为15%。图17、图18分别为两种工况下1轴和3轴的加速度时程曲线对比。表8汇总了各轴TMD减振效果。

表8 各轴竖向加速度峰值及TMD的减振效率Tab.8 Peak acceleration and TMD reduction effectiveness
5 结论和建议
通过对世博文化中心的理论分析和现场实测得出以下结论和建议:
(1)结构各榀桁架的竖向共振频率基本处于2.5 Hz-3.0 Hz之间,超出人正常行走频率范围,但是处于人快速走动和奔跑的频率范围内。
(2)当人正常行走时,结构竖向振动较小,TMD基本无影响;而当人以结构竖向共振频率快速走动或奔跑时,TMD能减小结构的竖向振动响应,减振效率约为15%。
(3)对第一振型为扭转且高阶竖向振动频率密集的长悬臂空间结构的动力特性,理论和实测结果有一定差异,需通过现场实测加深认识。
(4)对TMD这种频率敏感型减振装置,应通过现场实测了解结构的动力特性后再进行设计和调试。
(5)TMD能否有效的减小结构振动,不仅取决于TMD的固有频率是否与结构振动频率一致,也取决于施加的荷载频率是否与其一致。
[1] Figueiredo F P,Da Silva J G S,De Lima L R O,et al.A parametric study of composite footbridges under pedestrian walking loads [J].EngineeringStructures,2008,30:605-615.
[2]Zivanovic S,Pavic A,Reynolds P.Vibration serviceability of footbridges under human-induced excitation:a literature review[J].Journal of Sound and Vibration,2005,279(1-2):1-74.
[3] Ebrahimpour A,Sack R L.A review of vibration serviceability criteria forfloorstructures [J]. Computers &Structures,2005,83(28-30):2488-2494.
[4] BS 5400 - 2.Steel,concrete and composite bridges-part 2:specification forloads[S]. London:British Standard Institution,2006.
[5] ISO 2631-2.Mechanical vibration and shock-evaluation of human exposure to whole-body vibration-part 2:vibration in buildings(1 Hz to 80 Hz)[S].Geneva:International Standardization Organization,2003.
[6]何浩祥,闫维明,张爱林.人行激励下梁板结构与人体耦合作用研究[J].振动与冲击,2008,27(10):130-133.
[7]孙利民,闫兴非.人行桥人行激励振动及设计方法[J].同济大学学报(自然科学版),2004,32(8):996-999.
[8]徐庆阳,李爱群,张志强,等.考虑人体舒适度的大跨度悬挂结构振动控制研究[J].振动与冲击,2008,27(4):139 -142.
[9] AISC steel design guide series 11.floor vibrations due to human activity[S].Chicago:America Institute of Steel Construction,2003.

