尖晶石型ZnGa2O4光学性质的第一性原理计算

琚行松，张智慧

（1. 唐山师范学院 化工新材料与技术研究所，河北 唐山 063000；2. 邯郸市成安县第三中学，河北 邯郸 056700）

尖晶石型ZnGa2O4光学性质的第一性原理计算

琚行松1，张智慧2

（1. 唐山师范学院 化工新材料与技术研究所，河北 唐山 063000；2. 邯郸市成安县第三中学，河北 邯郸 056700）

首先采用基于密度泛函理论（DFT）框架下广义梯度近似平面波超软赝势法（包括PBE、PBESOL、PW91、RPBE、WC）对尖晶石型ZnGa2O4的结构进行了优化，得到和实验值最接近晶格常数a0=0.837 8 nm；然后在结构优化的基础上采用GGA-WC计算ZnGa2O4的电子结构和光学性质。结果表明，ZnGa2O4为间接带隙复合氧化物，带隙宽为2.335 eV；ZnGa2O4的静态介电常数为3.45，静态折射率为1.85，介电函数吸收边位于4.0 eV附近；ZnGa2O4的反射系数在19.3 eV附近取得最大值，吸收系数在11.0 eV～ 17.5eV间取值均较大，电子能量损失谱的共振峰在20.5 eV处，并与此能量时反射系数R(ω)的陡降相对应。

ZnGa2O4；第一性原理；能带结构；态密度；光学性质

1 引言

ZnGa2O4是最近研究得比较多的一种自激活型发光材料，在TFED，FED，VFD等诸多领域具有广阔的应用前景，比传统的硫化物发光材料在超高电场、电子轰击等极端条件下具有更好的化学稳定性，因而应用更为广泛[1,2]。

ZnGa2O4是由ZnO和Ga2O3组成的一种具有和尖晶石（MgAl2O4）同型的晶体结构的复合氧化物[3]，光学带隙约为4.4 eV，具有很高的化学稳定性，是一种很好的发光材料[3,5,6]，ZnGa2O4也被认为是一种新型n型半导体材料[4]。像其它宽能带半导体一样，在紫外光或低压电子的激发下，由于自我敏化作用，显示很强的蓝光发射[2]，能发出很纯的蓝色光。同时它本身也是一种很好的发光材料的基质，当掺杂不同的激活离子时，可得到红、绿、蓝等各种颜色的发光粉[6]。ZnGa2O4除了是一种具有潜力的发光材料，同时还是对还原性气体有高灵敏度的气敏材料。另外ZnGa2O4作为一类新型光催化剂，在光解水及光催化降解有机污染物方面表现出优异的光催化性能。薛珲和朱兰瑾[7]利用共沉淀法合成了具有中孔结构的尖晶石型ZnGa2O4纳米晶，其粒径小、比表面积大，光催化降解水杨酸的活性明显高于高温固相法合成的ZnGa2O4。紫外光辐照4.5 h ZnGa2O4纳米晶对水杨酸的降解率达到99.7%，其对水杨酸的光催化降解是通过强氧化物种含氧自由基和羟基自由基实现的。

量子力学第一性原理计算（即从头算）指仅根据基本的物理参数即可合理预测微观体系的状态和性质的计算方法[8]。近年来，第一性原理同分子动力学相结合，在材料设计、合成、模拟计算和评价等诸多方面都有着明显的进展，成为材料计算科学的重要组成部分。高速并行电子计算机的发展和先进的并行算法的开发，使得第一性原理计算对许多固体的电子结构和总能的运算得以实现，而且计算精度越来越高，效率也越来越高，可以计算的材料的范围也越来越广。

本文利用基于密度泛函第一性原理计算的方法，通过几何结构优化，得到ZnGa2O4的晶格参数。在此基础上，计算、分析ZnGa2O4的能带结构、态密度、分态密度，并对其介电常数、反射系数、吸收系数、损失函数、折射率等光学性质进行研究。

2 模型构建及计算方法

尖晶石型ZnGa2O4属于立方晶系结构[3,4]，空间群为(F3dm），晶胞参数a=b=c= 0.8335 nm，α =β=γ= 90°，晶胞中含有56个原子，其中Zn原子的原子占位为(0, 0, 0)，Ga原子的原子占位为(0.625, 0.625, 0.625)，O原子的原子占位为(0.388, 0.388, 0.388)，如图1所示。

图1 尖晶石ZnGa2O4的晶体结构模型

计算采用基于第一性原理密度泛函理论（Density functional theory）结合平面波赝势方法的Castep（Cambridge serial total energy package）软件包[9]。计算中，采用周期性边界条件，电子间的交换关联函数采用广义梯度近似（GGA）方法的多种函数形式（包括PBE、PBESOL、PW91、RPBE、WC），平面波截断能Ecut=380 eV。自洽场运算中，自洽精度设为每个原子能量收敛至5×10-7eV，原子间的作用力不大于0.01 eV/nm，第一布里渊区按5×5×5进行分格。获得优化晶胞结构后再进一步计算电子能带结构和光学性质。计算光学性质时，平面波截断能Ecut=600 eV，第一布里渊区按13×13×13进行分格，空带数设为16。分析光学性质时，剪刀差设为2.065 eV（取带隙的实验值与计算值的差值）。所有计算均在倒易空间进行。采用超软赝势（Ultrasoft Pseudopotentials，USP）描述离子实与价电子之间的相互作用，各元素外层价电子排布分别为：Zn（3d104s2），Ga（3d104s24p1），O（2s22p4）。

3 结果和讨论

3.1 几何结构优化

优化后得到的晶格参数列于表1，同时与实验值进行了对比。由表1可见，采用GGA-PBESOL和GGA-WC计算得到的晶格参数值与实验值偏差均不到0.6%，因此可取晶格常数a0为0.837 8 nm。

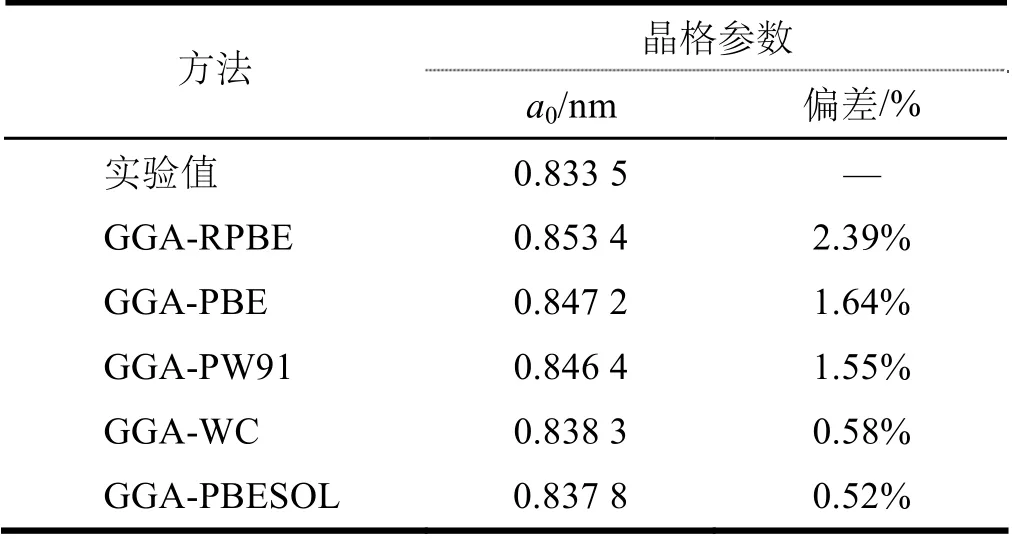
表1 ZnGa2O4的晶格参数计算值与实验值比较

3.2 ZnGa2O4电子结构

图2所示为ZnGa2O4在布里渊区沿高对称方向的电子能带结构。

图2 ZnGa2O4能带结构

由图2可见，ZnGa2O4价带的最高点（0 eV）与导带的最低点（2.335 eV）不在同一K点处，间接带隙宽为2.335 eV，与文献[3]中的4.4 eV相比明显偏小。一般认为，这种偏差主要是因为采用广义梯度近似（或局域密度近似）下的密度泛函理论计算基态能带时，对电子与电子之间的交换－关联能作用处理不足所导致的。但是，这并不影响对电子结构进行初步的理论分析。

文献[7]估算出ZnGa2O4的导带底和价带顶的位置分别为-1.42 eV和3.28 eV，其导带底位置比O2·（- 0.28 eV，NHE）的氧化还原势更负，价带顶比OH·/OH-（+ 2.27 eV，NHE）的氧化还原势更正，光生电子和空穴有能力与催化剂表面吸附的氧和水反应生成强氧化物种羟基自由基（OH·）或超氧自由基（·）。

图3所示为ZnGa2O4的总态密度（DOS）和分态密度（PDOS）。其中图(a)为ZnGa2O4的总态密度分布，(b)、 (c)、(d)分别为O、Zn和Ga的分态密度。由图可知，ZnGa2O4价带的低能级-19 eV～ -16 eV区域主要由O的2s电子构成，-13 eV～ -11 eV区域则主要由Ga的3d电子构成，价带的高能级-6 eV～ 0.5 eV区域主要是O的2p态及Zn的3d态贡献；导带的低能级2.5 eV～ 5.0 eV区域主要是Ga的4s态和Zn的4s态、4p态的贡献，导带的6 eV～ 11 eV区域主要是Ga的4s态和Zn的4p态贡献，除此之外还有Ga的4p态、Zn的4s态和O的2p态的贡献。尖晶石型ZnGa2O4具有良好的光催化性能，从其能带电子结构来看，其导带是由Ga的4s、4p，Zn的4s、4p及O的2p轨道杂化而成的，弥散度很大，光生电子在导带中有较高的迁移率，可抑制电子和空穴的复合，大量分离的光生电子和空穴有助于产生高的光催化效率。

图3 ZnGa2O4的总态密度和分态密度图

3.3 ZnGa2O4的光学性质

在线性响应范围内，固体的宏观光学响应函数通常可以由光的复介电函数

或复折射率

来描述，且

其中，ε1(ω)、ε2(ω)分别为复介电函数的实部与虚部，n(ω)为折射率，k(ω)为消光系数。

根据直接跃迁概率的定义和Kramers-Kronig色散关系可以推导出晶体的介电函数ε(ω)和复折射率N(ω)[10-12]：

式中，c和v分别表示导带和价带，e为电子电量，m为电子质量，h为普朗克常数，Δc为剪刀算子值的偏移量，BZ为第一布里渊区，K为倒格矢，|eMcv(K)|2为动量跃迁矩阵元，ω为圆频率，EcK和EvK分别为导带和价带上的本征能级。这些基本关系式反映了能级间电子跃迁产生光谱的发光机理，是分析晶体能带结构和光学性质的理论依据。

当光入射到媒质表面时，部分光被反射，若入射光强为J0，反射光强为J′，则有反射系数R=J′/J0。假定晶面方向平行于光轴，那么反射系数对频率的依赖关系将服从费米分布，可表示为[10]

当光进入媒质以后，由于部分被吸收，所以光强随进入媒质的深度x而指数衰减：

其中I为吸收系数，表示光在媒质中通过单位距离时光强度衰减情况，吸收系数随频率的依赖关系I(ω)可表示为：

电子能量损失谱（Electron energy loss spectroscopy，EELS）代表带电粒子以一定速度通过媒质时的能理损失，理论上电子能量损失谱定义为负的复介电函数的倒数虚部[11,13]，即

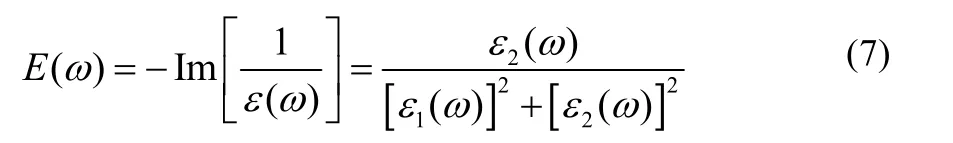
3.3.1 复介电函数与复折射率

图4所示为ZnGa2O4的复介电函数的实部ε1(ω)和虚部ε2(ω)随能量的变化关系。由图可知，在频率为0时复介电函数的实部ε1(0)=3.45，为ZnGa2O4的静态介电常数。随着光子能量的增加，复介电函数的实部存在两个极大值，分别位于5.0 eV和9.0 eV附近，在11.5 eV～20.75 eV间为负值。介电函数的虚部的吸收边位于4.0 eV附近，与价带顶到导带底的带间跃迁相对应；在10.6 eV附近取得最大值后逐渐减小，并于20.75 eV后趋于0。ε2(ω)在6.5 eV和10.6 eV附近有2个最大特征峰。

图4 ZnGa2O4晶体的介电函数

图5所示为ZnGa2O4的折射率与消光系数随能量的变化关系。由图可知，当ω=0时，n0=n(0)=1.85，为ZnGa2O4的静态折射率。折射率分别在5.0 eV和9.75 eV附近取得极大值。消光系数在11.5 eV附近取得最大值后逐渐减小，并于27.0 eV后趋于0。

图5 ZnGa2O4晶体的复折射率

3.3.2 反射系数、吸收系数与电子能力损失谱

图6、图7及图8所示分别为ZnGa2O4的反射系数、吸收系数及电子能量损失谱。

图8 ZnGa2O4晶体的电子能量损失谱

由图6可知，反射系数R(ω)随着能量的升高呈先增大后减小的趋势，在19.3 eV附近取得最大值，并于20.5 eV后迅速减小。

由图7可知，吸收系数I(ω)在11.0 eV～17.5 eV间取值均较大，表明能量位于该区间的光子较其它光子更容易被吸收，而且这样的光子能量范围比较宽泛。

由图8可知，ZnGa2O4晶体的能量损失谱E(ω)的共振峰在20.75 eV附近，此时能量损失最大，与反射系数R(ω)在20.5 eV后的急剧陡降相对应。

4 结论

（1）ZnGa2O4晶体具有明显的半导体能带结构特征，其带隙宽度为2.335 eV。价带的高能级-6 eV～ 0.5 eV主要是O的2p态及Zn的4d态贡献，导带的低能级2.5 eV～ 5.0 eV主要是Ga的4s态及Zn的4s态、4p的贡献。

（2）ZnGa2O4晶体的静态介电常数为ε1(0)=3.45，静态折射率n0为1.85。介电函数虚部ε2(ω) 的吸收边位于4.0 eV左右，在6.5 eV和10.6 eV附近有2个最大特征峰，并在20.75 eV后趋于0。

（3）ZnGa2O4晶体的反射系数R(ω)在19.3 eV附近取得最大值，并于20.5eV后迅速减小；吸收系数I(ω)在比较宽泛的11.0 eV～17.5 eV间取值均较大；能量损失谱E(ω)的共振峰在20.75 eV附近，与反射系数R(ω)在20.5 eV后的急剧陡降相对应。

[1]黄尚永,张希清,黄海琴,等.ZnGa2O4长余辉发光特性的研究[J].光谱学与光谱分析,2008,28(12):2777-2780.

[2]S L Mho, I K Jeong, Hong L P. Two self-activated optical centers of blue emission in zinc gallate[J]. Solid State Communications, 1998, 105(3): 179-183.

[3]J W Moon, H S Moon, E S Oh. Dependence of the structural and the optical properties of ZnGa2O4phosphors on the mixture molar ratio of ZnO and Ga2O3[J]. International Journal of Inorganic Materials, 2001, 3(6): 575-578.

[4]Yasuo Iida and Masaharu Okazaki. Characterization of Zinc Gallate Phosphors[J]. The Japan Society for Analytical Chemistry, 2001, 17: 1145-1146.

[5]Y Zhou, J Lin, M Yu, S Wang, H Zhang. Synthesis-Dependent luminescence properties of Y3Al5O12: Re3+(Re = Ce, Sm, Tb) Phosphors[J]. Materials Letters, 2002, 56: 628-636.

[6]于敏,林君,周永慧.柠檬酸-凝胶法合成ZnGa2O4: Mn2+/ Eu3+及其发光性能的研究[J].发光学报,2002,23(3):287-290.

[7]薛珲,朱兰瑾.尖晶石型ZnGa2O4纳米晶的制备及光催化性能[J].武汉理工学报,2010,32(23):22-26.

[8]张向超,杨华明,陶秋芬.TiO2基纳米材料第一性原理计算模拟的研究进展[J].材料工程,2008,1:76-80.

[9]Segall M D, Lindan-Philip J D, Probert M J, et al. First-principles simulation: ideas, illustrations and the CASTEP code[J]. Journal of Physics: Condensed Matter, 2002, 14(11): 2717−2744.

[10]沈学础.半导体光谱和光学性质(第二版)[M].北京:科学出版社,1992:76.

[11]马松山,徐慧,夏庆林.ZnRh2O4电子结构与光学性质的第一性原理计算[J].中国金属学报,2010,20(8):1623-1628.

[12]侯清玉,张跃,张涛.含氧空位锐钛矿TiO2光学性质的第一性原理研究[J].光学学报,2008,28(7):1347-1352.

[13]彭丽萍,徐凌,尹建武.N掺杂锐钛矿TiO2光学性能的第一性原理研究[J].物理学报,2008,56(3):1585-1589.

（责任编辑、校对：孙海祥）

First Principles Calculations of Optical Properties of Spinel ZnGa2O4

JU Xing-song1, ZHANG Zhi-hui2
(1. New Material & Technology Research Center of Chemical Engineering, Tangshan Teachers College, Tangshan 063000, China; 2. No. 3 Middle School of Chenan County in Handan, Handan 056700, China)

The generalized gradient approximation (including PBE, PW91, PBESOL, RPBE and WC) with plane wave ultrasoft pseudopotential based on the framework of density functional theory (DFT) was employed to optimize the structure of spinel ZnGa2O4. The calculated lattice constant of ZnGa2O4is 0.837 8 nm, which is the most close to the experimental one. Next the functional of GGA-WC was used to calculate the electronic structure and optical properties of ZnGa2O4. The calculation results show that ZnGa2O4is an indirect-band-gap semi-conductor with a wide-band gap of 2.335 eV. The static dielectric constant of ZnGa2O4is 3.45, the static refractive index is 1.85, and the absorption starts at about 4.0 eV. The reflectivity of ZnGa2O4reaches its highest point at 19.3 eV, the absorption is higher at from 11.0 eV to 17.5 eV, and the peak of the electron energy loss spectrum (EELS) is at 20.5 eV where there is an abrupt reduction in the the reflectivity.

ZnGa2O4; first principles; band structure; density of states; optical properties

O641

A

1009-9115(2012)05-0016-05

唐山市科学研究与发展计划项目（04360701B-14）

2012-4-15

琚行松（1972-），男，湖北黄梅人，博士，教授，研究方向为化工新材料与技术。