3G通信带通滤波器设计及优化

肖丙刚，叶 鹏，谢治毅

（中国计量学院 信息工程学院，浙江 杭州 310018）

3G通信即第三代移动通信技术是能把无线通信和网络等多媒体通信相结合的新一代通信系统，也是现在通信运营商重点发展的业务.3G系统的无线技术采用了高频段频谱资源以利于实现全球漫游，并支持多业务环境，展现了优良的网络灵活性和全覆盖能力.由国际电信联盟ITU提出的IMT－2000标准3G通信将统一采用2G频段，可用带宽达到230MHz，陆地网络和卫星网络分别分配了170MHz和60MHz.在城市地铁交通线路中的移动信号的引入及覆盖不免会遇到信号干扰等问题，通信系统中的前端设备滤波器在这里就起到很大的作用.

随着中国3G移动通信产业步入朝阳期，作为前端设备的滤波器也发展迅速.然而滤波器这类微波无源器件在当前设计和优化仿真过程中却有耗费时间、精确度低等缺点，与此同时一种称为空间映射算法的优化算法引入了器件设计中，利用空间映射算法在滤波器的设计中能够大大降低时间成本［1－8］.1994年加拿大学者 Bandler首次提出初始空间映射优化方法［1］，这种方法的核心思想就是将要优化的目标分为粗糙模型和精确模型两类模型.粗糙模型仿真时间很快但不够准确，而精确模型仿真准确但优化速度很慢.利用空间映射法连接这两个模型，将设计参数建立映射关系，使得利用设计参数能在两个模型之间相互迭代优化，结合这两类模型各自的优点，达到缩短优化时间、提高设计性能.为了更好的优化，1995年这个团队进一步提出了主动空间映射法［2］.之后各类新型空间映射算法相继提出，1998年提出置信域主动空间映射方法［3，4］，它要求迭代落在置信区间里来保证建立线性映射的可靠性，同时增加了参数提取的可靠性，保证了算法稳健性；但有负面影响，增加了算法的时间成本.1999年提出的混合迭代主动空间映射方法［6］，增强了算法的收敛性，减低了时间成本.2000年基于替代模型空间映射方法［7］，这种方法引入替代模型，高效优化了算法.2000年神经网络空间映射方法［8，9］，相比其它基于空间映射的优化方法，它不需要进行复杂的参数抽取过程来获取下一个迭代点，解决了非线性和多参数空间问题的能力.

2004年提出的隐式空间映射方法［10］充分利用了预选参数来建立粗糙模型和精确模型间的映射，通过对预选参数进行参数提取来得到替代模型，随着替代模型的建立，粗糙模型和精确模型的映射关系也得到更新［10，11］.本文通过设计平行耦合带通滤波器，利用隐式空间映射算法来缩短优化时间［12，13］，最 终 设 计 出 带 通 滤 波 器 中 心 频 率 为2GHz，带宽为260MHz.在1.87～2.13GHz内插入损耗小于2.5dB，带内波纹小于0.5dB.在小于1.75GHz和大于2.3GHz的频带上带外抑制大于20dB，其通带满足我国三种类型3G手机信号频段.

1 隐式空间映射法

隐式空间映射算法的映射关系表征不是特别明显，可能隐藏在粗糙模型中.通过迭代，由优化粗糙模型来获得与符合精确模型的新预选参数来改变粗糙模型.再通过固定预选参数优化所选参数来变化粗糙模型，最后再根据新的设计参数来优化精确模型.结果满足指标则停止，否则继续迭代.现在定义精确模型在设计参量xf的响应为Rf，一般优化问题可以表示为：

其中Rc（xf，x）代表粗糙模型响应，xc和x分别为设计参量和预选参数，Rc（xf，xj）是隐式空间映射在预选参数xj下的响应矢量，xj为第j次参数提取的预选参数的值.

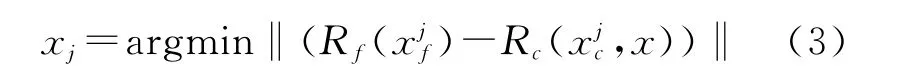
（3）式的含义为改变了预选参数的粗糙模型响应与精确模型响应相匹配，其示意图如图1.

图1 隐式空间映射示意图Figure 1 Implicit space mapping diagram

2 带通滤波器设计及仿真

2.1 原始参数

用传统方法设计平行耦合带通滤波器根据设计指标求出原始参数，先确定设计指标.中心频率为2GHz，相对带宽为260MHz，插入损耗小于2.5dB（1.88GHz≤ω≤2.15GHz），阻带的带外抑制大于20dB（ω≤1.75GHz，ω≥2.28GHz），通带内带内波纹小于0.5dB.根据设计指标选择低通滤波器原型为0.5dB等波纹滤波器，由图得滤波器所需最少阶数为4阶，即N＝4，再由表得原型的元件值为g1－g5.通过带通滤波器的设计公式为：

结果如表1.再通过ADS微带线计算工具LineCalc确定微带线几何尺寸：微带线宽度W，间隙S以及长度L.由于终端电容的影响，一般长度L要减去0.33 h，h为介质基板的厚度.由此可以得到滤波器设计的原始参数.

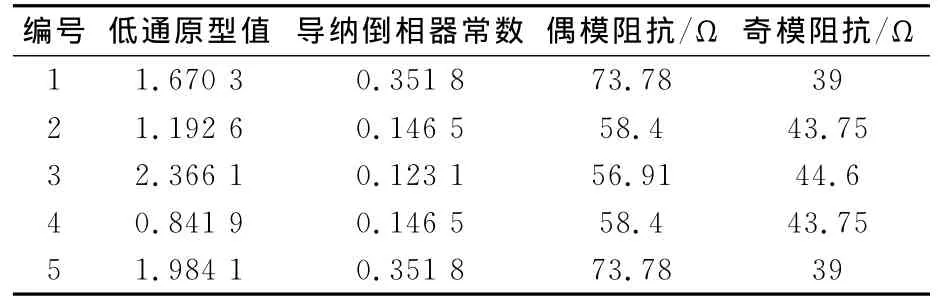
表1 各段耦合传输线偶模和奇模的特征阻抗Table 1 Characteristic impedance of even mode and odd mode in each coupling transmission line

2.2 粗糙模型建立

运用ADS电路仿真软件根据上述耦合微带线的几何参数建立带通滤波器的模型，如图2.这时设定基板厚度初始值为2mm，介电常数初始值为9.8，金属导带厚度为0.018mm.

图2 平行耦合带通滤波器ADS模型Figure 2 Parallel coupled bandpass filter model of ADS

通过S参数仿真得到图3结果，在此发现与指标要求相差较大.

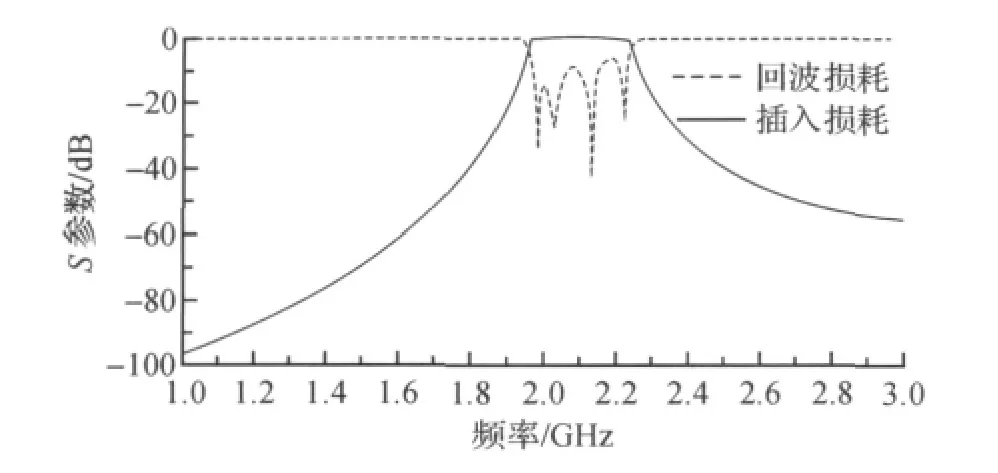
图3 ADS模型原始仿真结果Figure 3 ADS simulation results of the original model

将各耦合微带线宽度、间隙和长度作为初始的优化参数进行优化，得到较好的S参数仿真效果.由于耦合微带线的对称性数据简化为3组.设粗糙模型中的初始参数为：

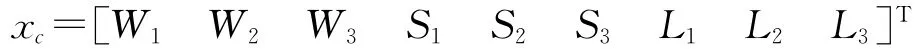
仿真优化结果如下图4.

2.3 精确模型建立

运用HFSS电磁仿真软件建立平行耦合带的全波模型，如图5.基板所选用的材料为氧化铝陶瓷，板材厚度、介电常数和金属导带厚度与ADS中初始一样.将ADS中初始参数带入HFSS模型中并仿真计算S参数得到图6有明显的

图4 ADS模型优化后仿真结果Figure 4 ADS simulation results of the optimized model

频率偏移.这时精确模型中参数为：

图5 平行耦合带通滤波器HFSS模型Figure 5 Parallel coupled bandpass filter model of HFSS

图6 将ADS数据直接放入HFSS中仿真结果Figure 6 Simulation results in HFSS used the data of ADS

3 隐式空间映射法仿真优化过程

在上述粗糙模型和精确模型的确立中已经对平行耦合带通滤波器进行了初步的设计，再运用空间映射法进行优化.首先确定粗糙模型的优化变量为带通滤波器各耦合线的宽度、间隙及长度，即上述所设的xc.其次是预选参数的设置，将滤波器耦合线的厚度和介电常数设置为参数提取变量x：

由于设计的各段耦合线存在对称性，h1、h2、h3和εr1、εr2、εr3分别代表前三段耦合线的厚度和介电常数.如图7为ADS中优化模型，图8为ADS参数提取模型.

图7 平行耦合带通滤波器ADS优化粗糙模型Figure 7 Optimization coarse model parallel coupled bandpass filter in ADS

在上述精确模型的建立就已经完成最初的两个模型的优化设计，精确模型优化后并不能满足原定的指标，开始进行参数提取：

图8 平行耦合带通滤波器ADS参数提取模型Figure 8 Parameter extraction model parallel coupled bandpass filter in ADS

将第一次参数提取后的预选参数值带回粗糙模型，如图7.保持预选参数不变，将粗糙模型中的参数x0c进行优化，得到更优的参数值，即第一次迭代的参数，再带入精确模型中优化.第一次迭代结果如图9.

图9 第一次迭代HFSS精确模型优化结果Figure 9 First iteration of an accurate model to optimize the results of HFSS

由图9可以看出第一次迭代并不是十分符合设定的技术指标，再进行多次迭代.由图10可以看出经过前四次迭代后，滤波器的仿真效果都有不同的改良.在第二次迭代时最为接近设定的技术指标，后来的几次迭代优化结果都没有第二次迭代效果理想，第三次和第四次迭代的回波损耗在截止频率的下降较为缓慢，而第五次迭代已经开始偏离设定的技术指标，这是因为在粗糙模型优化过程中存在不稳定性.在这里选取第二次结果作为最终结果.

图10 各次迭代HFSS精确模型优化结果比较图Figure 10 Iteration of the optimization results of HFSS comparison accurate model（a）Return loss；（b）Insertion loss

第二次结果由图10中实线表示，由此可以得到精确模型的最终参数值：

确定滤波器的几何尺寸.最终仿真结果在图11中给出.

由图11可以看出最终的滤波器优化结果基本符合原先定下的设计指标，在3G移动通信频段1850MHz到2150MHz插入损耗小于3dB，回波损耗都在大于10dB，带内波纹小于0.5dB.在阻带大于2.3GHz和小于1.75GHz的频段插入损耗大于20dB.优化过程经过两次迭代就能达到很好的效果，有效地节省了时间成本.

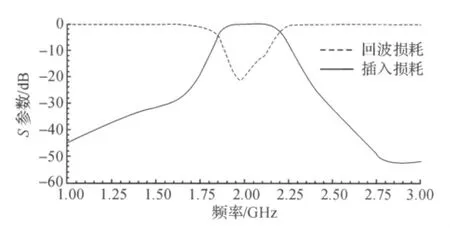
图11 最终滤波器优化结果Figure 11 Final filter optimization results

4 结 语

通过隐式空间映射法在HFSS和ADS软件分别建立了精确模型和粗糙模型.隐式空间映射法在优化过程中运用加快了优化的速率并提高了优化的精度，同时也验证了空间映射算法的高效性，在微波器件优化中起到了很大的作用.最终精确模型仿真结果中1850MHz到2150MHz频段插入损耗小于3dB，回波损耗大于10dB.在频段小于1.75GHz的下阻带和大于2.3GHz的上阻带中带外抑制都大于20dB.平行耦合带通滤波器满足三种通信制式在3G网络中的传输需求.

［1］EKSTROM H，FURUSKAR A，KARLSSON J.Technicalsolutions for the 3Glong－term evolution［J］.Communications Magazine，IEEE，2006，44（3）：38－45

［2］BANDLER J W，BIEMACKI R M，CHEN S H.Space mapping technique for electromagnetic optimization ［J］.IEEE Transactions on Microwave Theory and Techniques，1994，42（12）：2536－2544

［3］BANDLER J W，BIEMACKI R M.Electromagnetic optimization exploiting aggressive space mapping ［J］.IEEE Transactions on Microwave Theory and Techniques，1995，43（12）：2874－2882

［4］BANDLER J W，BIEMACKI R M，CHEN S H.Space mapping optimization of waveguide filters using finite element and mode－matching electromagnetic simulators［J］.International Journal of RF and Microwave Computer－Aided Engineering，1999，9：54－70

［5］BANDLER J W，BIEMACKI R M，CHEN S H.Design optimization of interdigital filters using aggressive space mapping and decomposition［J］.IEEE Transactions on Microwave Theory and Techniques，1997，45（5）：761－769

［6］BAKR M H，BANDLER J W，GEORGIEVA N K，et al.A hybrid aggressive space－mapping algorithm for EM optimization［J］.IEEE Transactions on Microwave Theory and Techniques，1999，47（12）：2440－2449

［7］BAKR M H，BANDLER J W，MADSEN K，et al.Space mapping optimization of microwave circuits exploiting surrogate models［J］.IEEE Transactions on Microwave Theory and Techniques，2000，48（12）：2297－2306

［8］BANDLER J W，ISMAIL M A，RAYAS J E，et al.Neuromodeling of microwave circuits exploiting space mapping technology［J］.IEEE Transactions on Microwave Theory and Techniques，1999，47（12）：2417－2427

［9］BAKR M H，BANDLER J W，ISMAIL M A，et al.Neural space－mapping optimization for EM－based design ［J］.IEEE Transactions on Microwave Theory and Techniques，2000，48（12）：2307－2315

［10］BANDLER J W，CHEN S H，NIKOLOVA N K，et al.Implicit space mapping optimization exploiting preassigned parameters［J］.IEEE Transactions on Microwave Theory and Techniques，2004，52（1）：378－385

［11］KOZIEL S，MENG J，BANDLER J W.Accelerated microwave design optimization with tuning space mapping［J］.IEEE Transactions on Microwave Theory and Techniques，2009，57（2）：383－394

［12］罗昌桅，叶 强，王 娜.同轴腔体双频合路器设计与实现［J］.中国计量学院学报，2010，21（3）：227－231

［13］赵吉祥，曾江波.SOC中的平面拐线的等效电路［J］.中国计量学院学报，2006，4（17）：296－299.