基于PSO算法和IE3D仿真软件的滤波器设计
方 圆,尤志刚,朱臣伟,钱兴成
(南京电子器件研究所,南京 210016)
1 引言
从通信发展的历史来看,滤波器一直起着相当重要的作用,差不多所有的微波接收机、发射机和微波实验装备都要求设备具有滤波功能,滤波器的性能也随着通信技术的发展而取得不断的提高。上个世纪早期,多路通信系统的技术革命开创了电信的新纪元。这种新的通信系统要求在特定的频带内发射及接受信号,而且多路系统要求将频域分成不同的频带,这就对滤波器提出了很高的要求。
带通滤波器是滤波器中使用最多、最重要也是最难设计的一种滤波器。作为一种体积小、重量轻和可靠性高的微波集成电路(MIC)单元[1~2],微带带通滤波器在电子系统尤其是通信领域被广泛应用。随着微波技术的发展,微带滤波器的种类日益增多。他们性能各异,设计方法也有所不同。
另一方面,滤波器的小型化已经成为一个热门的研究领域,在小型化的基础上提高性能是滤波器研究的主要内容。每年在各相关杂志上可以看到许多有关如何减小滤波器的体积和优化其性能的文章。可以说在滤波器小型化和性能优化这一领域还有很多问题有待进一步探索和解决。
高频双通带滤波器在很多方面都有很大的用途,但目前研究较少。Hairpin结构目前已经得到了比较充分的认识,但用于双通带的较少。鉴于此,本论文设计了一个采用可变特性阻抗的Hairpin耦合结构的高频双通带滤波器,在很小的面积上使滤波器的性能达到了很好的要求。
2 原理介绍
2.1 低通滤波器原理
根据滤波器的插入衰减特性,可以将滤波器分成低通、高通、带通和带阻四种滤波器,图1中串联支路是电感,并联支路是电容;频率越低,电感的分压作用和电容的分流作用就越小,因此负载吸收的功率就越多,形成了低通的衰减特性,这是低通滤波器。
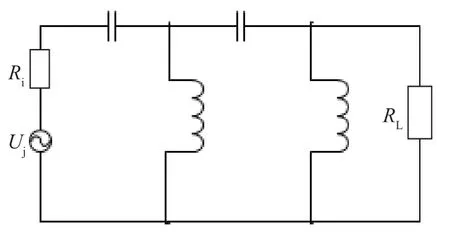
图1 低通滤波器电路
理想的低通滤波器的衰减特性为:在ω=0到ω1的频率范围内,衰减为0,称为通带,在ω>ω1的范围内衰减为∞,称为阻带。ω表示角频率,ω1称为截止频率。显然,这种理想的滤波特性,用有限个元件的电抗网络是无法实现的,因为有限元件数的电抗网络的衰减特性一定是连续函数,不可能在某一频率上突跳。实际的滤波器只能逼近理想滤波器的衰减特性,因此,在综合设计滤波器时,首先要确定一个逼近理想衰减特性的衰减函数句加,然后再根据这个逼近函数综合具体的电路结构来。最广泛使用的逼近函数有三种,相应的滤波器称为最平坦型、切比雪夫型和椭圆函数型。
2.2 频率变换
在低通原型中频率是关于截止频率ω1归一的,而元件值是关于源内电阻归一的。所以低通原型可以完成截止频率为1、源内阻也为1的低通滤波器。实际的滤波器不仅截止频率和源内阻不一定为l,通带特性也不一样。除了低通外,还有高通、带通和带阻。不过,利用频率变换和阻抗变换可以从低通原型的元件值得到任何一种实际的滤波器结构和原件值。
为了从带通滤波器变换成低通原型的衰减特性,可以采用频率变换函数:
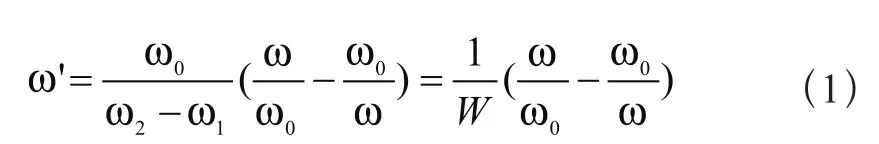
式中ω2为带通滤波器上边带截止频率,ω1为带通滤器下边带截止频率,称为中心频率,称为相对带宽[3]。
经过相应的频率变换和函数变换可以得到带通滤波器串并联支路的电感和电容的实际滤波元器件值。由于篇幅原因,相应的变换过程在此不再赘述。
2.3 PSO粒子群优化算法
粒子群优化算法(PSO)是一种进化计算技术(evolutionary computation),由Eberhart博士和Kennedy博士发明,起源于对蜂群、鸟群或鱼群寻食过程的模拟[4~5]。PSO是一种新型的优化算法,但是它已经得到了广泛关注和深入的研究。在基本PSO算法的基础上,已经出现了各种有意义的改进PSO算法。Robinson和Rahmat-Samii将该算法运用到天线设计的领域,证明了粒子群算法在多维、线性、非线性等问题上的高效性。
PSO初始化为一群随机粒子(随机解)。然后通过叠代找到最优解。在每一次叠代中,粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解。这个解叫做个体极值pBest,另一个极值是整个种群目前找到的最优解。这个极值是全局极值gBest。另外也可以不用整个种群而只用其中一部分作为粒子的邻居,那么在所有邻居中的极值就是局部极值。在找到这两个最优值时,粒子根据如下的公式(2)、(3)来更新自己的速度和位置:

v[ ]是粒子的速度,present[ ]是当前粒子的位置。pbest[ ]和gbest[ ]如前定义。rand ( ) 是介于(0,1)之间的随机数,c1和c2是学习因子,通常c1 = c2 = 2。
3 滤波器的优化
3.1 滤波器的原型
Hairpin耦合结构滤波器是一种体积小、重量轻的平面滤波器,能够很好地满足现代滤波器的要求,故得到了广泛的应用。
本章中滤波器的原型为一个具有可变特性阻抗的Hairpin耦合结构滤波器,其结构如图2所示。

图2 Hairpin耦合结构滤波器
图中介质基片的高度h=0.254mm,相对介电常数εr=2.2,损耗角正切为tan δ=0.005。金属带的厚度h=0.003mm,导电率为4.1×107s/m。
如图2所示,滤波器的结构非常紧凑,面积仅为5.5mm×2.7mm。但实现了高频双通窄带滤波的作用。仿真曲线如图3所示。可以看出以下几点:
(1)第一个通带的S21最高为-3.38dB,而第二个通带的S21最高为-4.43dB,两者相差了1.05dB。
(2)两个通带的带内非常不平坦。
(3)两个通带的S11的零点位置不接近,这个规律也可由得出。而且两个通带的S11只在-8dB左右。
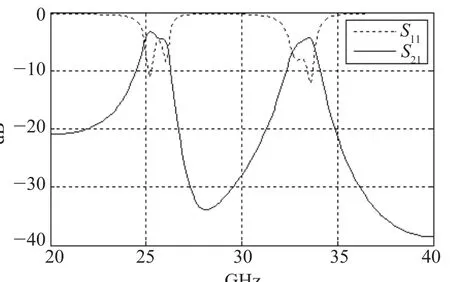
图3 滤波器的仿真曲线
3.2 优化方案
基于PSO算法和IE3D的优点,我们提出了一种利用MATLAB和IE3D的联合优化方案,具体方案为:将滤波器结构中的一些参数作为PSO的“粒子”,由粒子群算法对其进行优化,同时设定适应度函数,根据所得到的适应度值不断更新粒子的速度和位置,直到满足循环结束条件。电磁场仿真软件IE3D在每次循环中调入粒子位置矢量,完成对适应度函数参数的计算,返回给粒子群算法,计算适应值,实现了循环调用过程。
本算法优化程序通过MATLAB中的PSO优化程序不断调用IE3D来实现。根据程序各个部分作用的不同,可以将程序分成三个模块:PSO运算模块,IE3D接口模块,IE3D仿真模块。IE3D接口模块位于粒子群运算模块和IE3D仿真模块之间,主要功能是从粒子群运算模块中接受粒子群中粒子的位置参数(有待优化的结构参数),并传送给IE3D软件;当IE3D完成仿真,将作为结果输出的适应度函数参数值(有待优化的性能参数)回馈给粒子群运算模块,IE3D运算模块每次接受不同的结构参数,并针对具体结构进行仿真。
3.3 对滤波器的依次优化
鉴于上面提到的滤波器的仿真曲线不理想,下面我们对滤波器原型的几个指标进行改变,希望从中找出规律,为人工和程序优化[6]打下基础。
3.3.1 输入输出臂的宽度a的优化
由相关知识可知,改变输入输出的特征阻抗,可以显著优化S11的效果,同时改变通带内波形的形状和相关参数。分别测出当a=0.1、a=0.15、a=0.25时滤波器传输系数S21的曲线和反射系数S11的曲线,如图4、5所示。
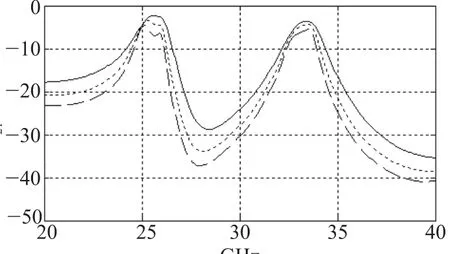
图4 a取不同值时对S21的影响
从图4中可以大致看出当输入输出臂的宽度a变宽时带宽变宽,通带内的平坦度变好,但陡峭度变差;同时图5中随着输入输出臂a的变宽S11变化非常显著,特别当a=0.25时第一个通带的S11降到了-17dB左右,同时第二个通带的S11降到了-30dB左右,而且S11零点很均匀。另外第二个通带的S11好于第一个通带的S11。
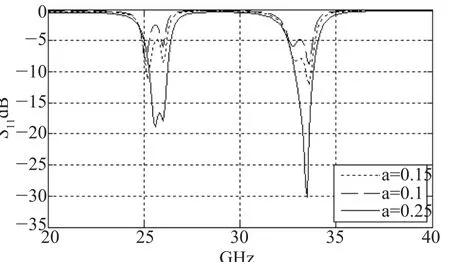
图5 a取不同值时对S11的影响
3.3.2 耦合带长度b的优化
两个耦合臂之间相当于一个电容,与耦合之间的距离有关,同时也与臂的长度有关。本节中假设耦合之间的距离为0.1mm,改变臂的长度,观察宽度b的变化对滤波器传输系数S21的影响。同时耦合臂长度的变化也影响特性阻抗。图6为当b=0.15、b=0.25、b=0.35时滤波器传输系数S21的仿真曲线。

图6 耦合臂的长度b对S21的影响
从图6中可观察出随着耦合臂b的加长,第一个通带的带宽变宽,陡峭度变差,平坦度变差。同时当b=0.35时,两个通带的S21很平坦,而且很接近,同时陡峭度也非常好。
3.3.3 Hairpin耦合支长度c的优化
Hairpin耦合支长度c对滤波器的中心频率有影响,由理论可知上述滤波器原型中的上面Hairpin耦合支决定第一个通带的中心频率。耦合之间相当于电容,耦合的长短决定电容的大小,电容的大小又体现为对一些频率的抑制更好,一些频率的选择性更好,因此对两个通带内的S11有影响。改变Hairpin耦合支长度c的大小测得当c=0.7、c=0.9、c=1.1时滤波器传输系数S21的曲线和反射系数S11的曲线分别如图7、8所示。
从图7中可以看出随着长度c的增加,第一个通带明显向左移动,即中心频率在减小,这可以很容易从理论中分析出来:由于其他参数(εre,ω,h,t等)不变化,只是长度变化,故特性阻抗不变,又由于一般长度为谐振频率的,由公式:

可知谐振频率与中心频率成反比,即谐振长度的增加意味着中心频率的下降。同时图8中随着长度c的增加陡峭度和平坦度变得更好,但是两个通带的插入损耗差距增大。
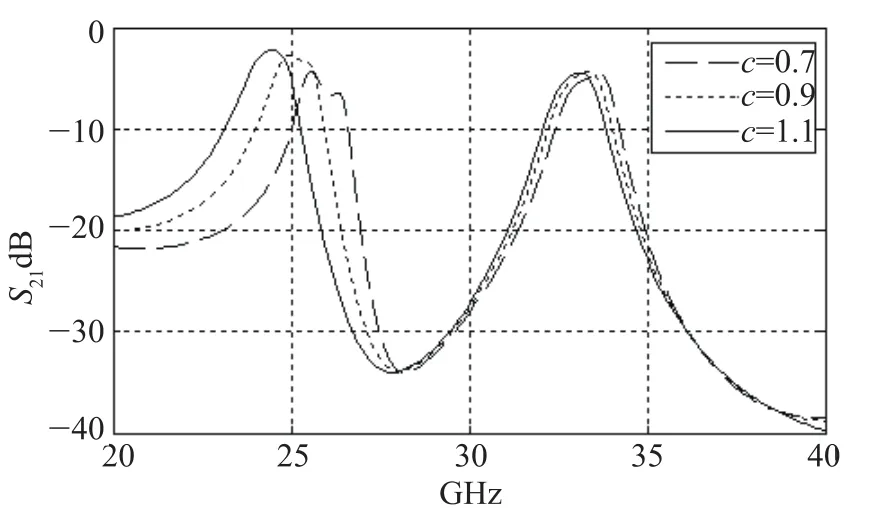
图7 Hairpin耦合支长度c对S21的影响

图8 Hairpin耦合支长度c对S11的影响
耦合支之间相当于电容,耦合的长度决定电容的大小,电容的改变表现为对一些频率的选择性更好,对一些频率的抑制性更好。从图8中我们可观察出随着长度c的增加,两个通带的S11变化非常显著,特别当c=1.1时第一个通带的S11下降到了-35dB。另外第一个通带的S11明显好于第二个通带的S11。
3.3.4 长度d、e的优化
由于下面的耦合支影响第二个通带的中心频率,同时耦合长度的变化又对一些频率的选择性更好,在此我们假定d=e,图9、图10分别表示当d=0.4、d=0.55、d=0.7时滤波器传输系数S21和反射系数S11的曲线。
从图9中可以观察出随着长度d的减小,第二个通带的中心频率增加,具体原因已经在3.3.3节中分析过了。图10中随着长度d的增加第一个通带的S11效果变差,即长度d越小S11效果越好。同时第一个通带S11的效果明显好于第二个通带S11的效果。这需要以后继续调整结构以便使两个通带的S11的效果差距不大,即两个通带的插入损耗控制在可接受范围内,同时应使两个通带的S11的效果满足要求。

图9 d对滤波器传输系数S21的影响
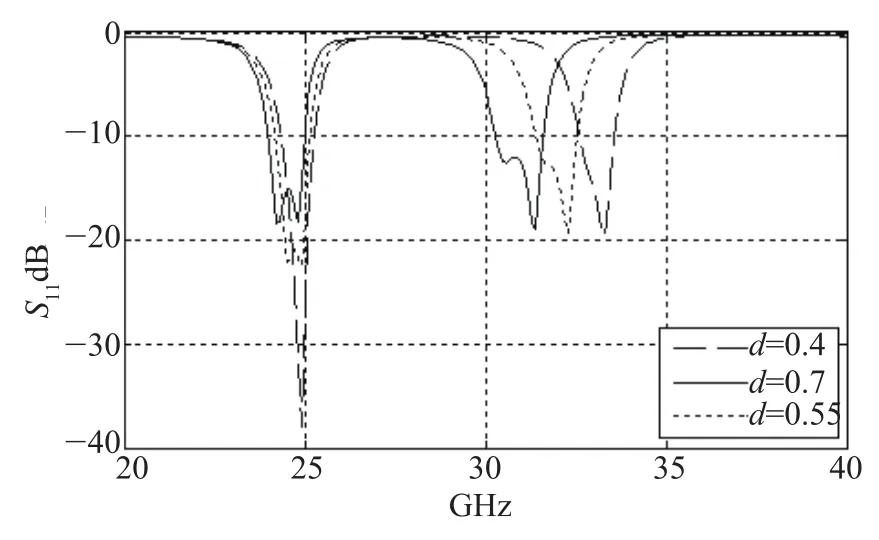
图10 d对滤波器反射系数S11的影响
3.3.5 长度f的优化
我们知道耦合微带线的奇模、偶模通过公共接地板产生的耦合效应,这种耦合效应导致了奇模特性阻抗和偶模特性阻抗。奇模特性阻抗和偶模特性阻抗与两个耦合微带线的结构和尺寸有关。如图2所示的滤波器结构,对两个耦合结构进行改变,即改变了微带线的奇模特性阻抗和偶模特性阻抗,表现为对通带的选择性更好,其仿真曲线的比较如图11所示。
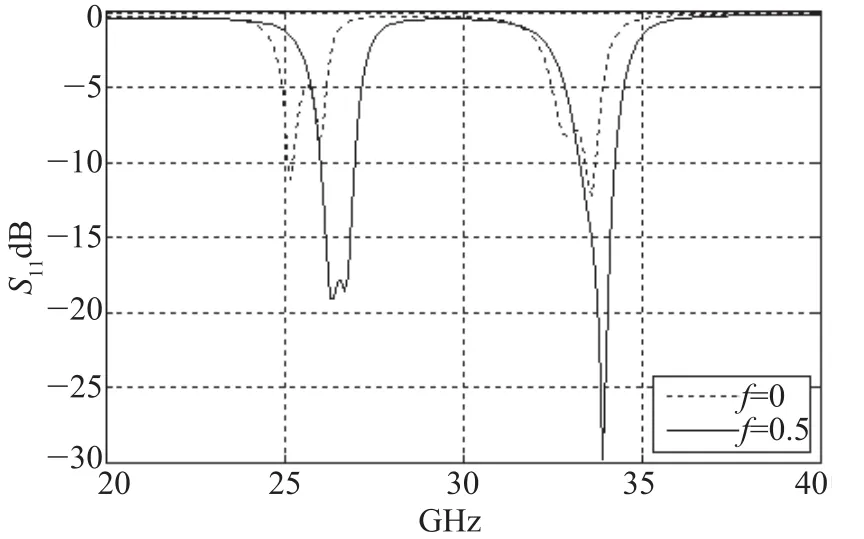
图11 耦合结构发生变化时S11的比较曲线
图11中对耦合结构进行了改进,S11变化明显,第一个通带的S11下降到了-17dB,第二个通带的S11效果非常好,下降到了接近-30dB左右。但是两个通带的S11不平衡,表现为两个通带的插入损耗差距太大。
耦合结构的改进明显提高了滤波器S11的效果,同时如前所述,尺寸的改变同样可以影响奇模特性阻抗和偶模特性阻抗,对滤波器传输系数S21和反射系数S11的效果同样有影响,图12和图13分别表示当f=0.5、f=1、f=1.5时滤波器传输系数S21的曲线和反射系数S11的曲线。
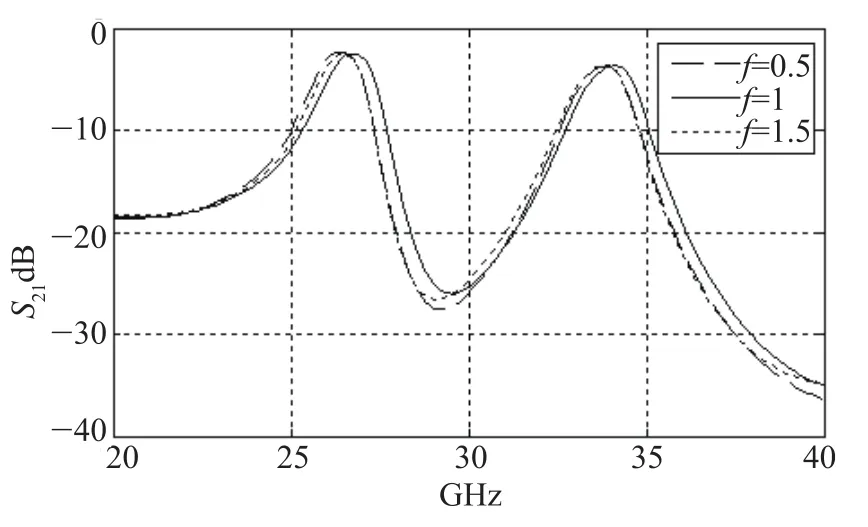
图12 f对滤波器传输系数S21的影响
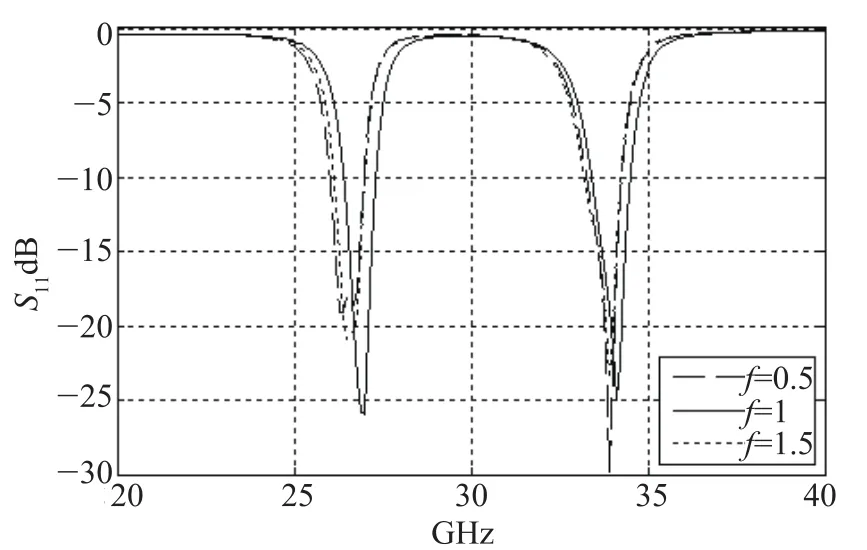
图13 f对滤波器反射系数S11的影响
从图12、图13中可以看出,当f太大或太小时S11的效果都不好,相反当f=1时的效果好于f=0.5、f=1.5时的效果,这可以理解为耦合尺寸与谐振点的对应问题,一个谐振点对应一个耦合尺寸,为了找出这个耦合尺寸,后面的章节会采用PSO算法对f进行优化。
3.3.6 微带线阶梯长度g的优化
如图2所示,将图中的一段微带线改成阶梯型,微带线阶梯的不连续性产生高次模。根据对偶定理,这种不连续性可等效为串联电感,也可等效为并联电容,从而对原来的电路产生影响。图14中表示了将一段微带线改成阶梯后与未改之前的效果比较。
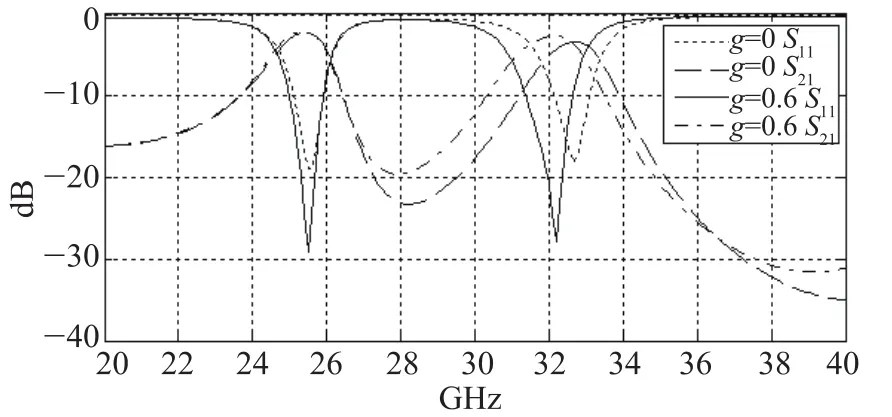
图14 微带线阶梯的效果比较
从图14中可以看出,将微带线改成阶梯形式后S11下降非常厉害,两个通带的S11都大约下降了-10dB左右,改善效果明显。另一方面,对结构进行改进后S21也有改进,如图14所示,结构进行改进后第二个通带的S21提高了-0.7dB左右,这样使得第二个通带的S21更接近第一个通带的S21,两者仅相差不足-0.5dB。
从上面的分析和仿真中都能看出,将微带线改成阶梯形后滤波器的效果得到明显改进,下面分析当g取不同值时(g=0.4、g=0.6、g=0.9)滤波器传输系数S21和反射系数S11的效果,分别如图15和图16所示。
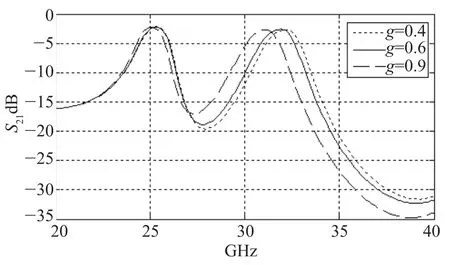
图15 微带线阶梯长度g对S21的影响
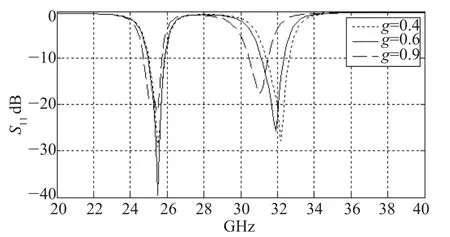
图16 微带线阶梯长度g对S11的影响
从图15中可以看出,当g取不同值时第二个通带的插入损耗相差不大,但当g=0.4时的陡峭度较好。另一方面,从图16中可以反映出当g=0.9时S11的效果不理想;当g=0.6时第一个通带的S11降到了接近-40dB,而第二个通带的S11只有-25dB;当g=0.4时两个通带的S11很接近,都达到了-28dB。
3.3.7 耦合臂宽度h的优化
按照图2所示的滤波器结构,耦合臂的宽度h不仅影响特性阻抗,而且影响耦合之间的关系,可知改变耦合臂的宽度必然对滤波器造成影响。图17表示当h=0.1、h=0.2时滤波器的S11的比较。
图17中h=0.1时的S11明显好于h=0.2时的S11。在上面的分析中可知,耦合臂宽度的改变就改变了奇、偶模的特性阻抗,从而对两个通带频率的选择性更好,反映出来就是S11结果更好。
3.3.8 基于PSO算法和IE3D程序对滤波器的综合优化
以上我们详细分析了滤波器原型中一些结构和参数的改变对滤波器传输系数S21和反射系数S11的影响,使我们对滤波器原型有了一定的认识,这为我们下面的优化提供了理论依据。
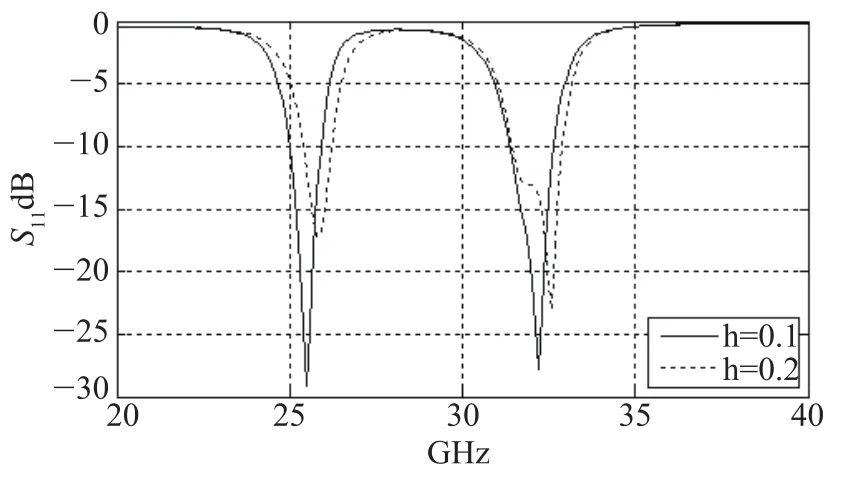
图17 耦合臂宽度h对S11的影响
现在我们利用PSO算法和IE3D的联合程序对图2中的参数(a、b、c、d、e等)进行优化,同时考虑到加工精度的问题,因此间距最小取0.1mm,优化的结果如下。
滤波器的最终结构和尺寸如图18所示,图18中对一些参数进行了标注,滤波器的大小为5.5mm×2.7mm,其仿真曲线如图19所示。

图18 滤波器的最终结构

图19 滤波器最终结构的仿真曲线
从仿真曲线S21可以看出,两个通带的平坦度较好,而且第一个通带的插入损耗为-2.1dB,第二个通带的插入损耗为-2.6dB,两者仅相差0.5dB,另外陡峭度也较好;另一方面,两个带内的S11都下降到了-28dB左右,可以很好地满足要求。
4 结论
设计了一个Hairpin耦合结构的带通滤波器,并通过PSO算法及IE3D程序进行了联合优化,并得到较好的技术指标,最终滤波器的大小仅为5.5mm×2.7mm,实现了26GHz和32GHz的双通带,且两个带内的S11都下降到了-28dB左右,效果比较理想。
[1] F. J. Winter, J. J. Taub, M. Marcelli. High dielectric constant strip line band pass filter[J]. IEEE Trans,1991, 2182-2187.
[2] P. Pramanil. Compact 900-MHz hairpin-line filters using high dielectric constant microstrip line[J]. IEEE MIT-S.Digest, 1993, 885-888.
[3] Hui-Wen Yao, Kawthar A.Zaki, Ali E. Atia, Rafi Hershtig.Full Wave Modeling of Conducting Post in Rectangular waveguides and Its Application to Slot Coupled Combline Filters[J]. IEEE Trans, 1995,43(12):2824-2829.
[4] M. Clerc, J. Kennedy. The particle swarm—explosion,stability and convergence in a multidimensional complex space[J]. IEEE Trans, 2002,6(1):58-73.
[5] Y. Shi, R. Eberhart. Empirical study of particle swarm optimization[J]. in Proc. Cong. Evol. Comput, 1999,3:1945-1950.
[6] Chu-Yu Chen, Cheng-Ying Hsu. A Simple and Effective Method for Microstrip Dual-Band Filters Design[J]. IEEE Microwave And Wireless Components Letters, 2006.

