一种基于频差补偿的相位谱时延估计方法

邱 天 爽， 尤 国 红， 沙 岚， 赵 小 平， 高 阳

（大连理工大学 电子信息与电气工程学部，辽宁 大连 116024）

0 引 言

时延估计是无源时差定位系统中的关键技术，时差定位因其隐蔽性高、定位速度快等优点广泛应用于军事和民用领域中，如雷达、电子战及基于位置的服务等.近几十年来，时延估计的方法不断得到发展和创新，从时域经典的相关类方法[1、2]到频域的相位谱法[3、4]，从LMS自适应法到ETDE及各种衍生的自适应类算法[5、6]，从传统的二阶累积量法到高阶及分数低阶累积量法等[7、8].

然而众多的时延估计方法中，专门针对射频窄带信号的有效方法却不多.影响射频窄带信号时延估计精度的主要因素包括：（1）两台独立接收机的本振频率无法保证一致，导致两路接收信号之间的中频偏差总是存在的，而目前的时延估计方法很少考虑中频偏差对估计精度的影响；（2）一般来说，射频窄带信号具有采样频率较高、绝对带宽较小的特点，因而相对带宽（绝对带宽与采样频率之比）就较小，如采用相位等频域内的方法估计时延，可利用的有效点数较少，信息量较小，时延估计的精度难以得到保证；（3）窄带信号的相关函数所占频带较宽，受噪声影响较大，从而产生较大的时延估计误差.

本文针对影响射频窄带信号时延估计精度的3个主要因素，采用平方倍频法估计出两路信号的中频，相减得到中频偏差，然后采用频差补偿方法消除中频偏差对后续时延估计精度的影响；利用线性调频Z变换（CZT）代替离散傅里叶变换（DFT）求取两路接收信号的互功率谱密度，在有限带宽内增加时延估计的有效点数；同时考虑到相位谱时延估计法的特点，即两路信号的相位谱变化规律呈线性，建立简单的Kalman滤波模型对相位谱进行线性拟合，改善信噪比，从而提高时延估计的精度.

1 方法介绍

1.1 问题描述

假设某一射频窄带源信号被两个独立的接收机接收，由于接收机之间存在一定的空间距离，接收到的两路信号之间存在一定的时差，设两路接收信号的双基元离散模型为

式中：x（n）和y（n）为接收到的信号；s（n）为射频窄带源信号；v1（n）和v2（n）为与源信号互不相关的加性独立高斯白噪声；D为x（n）与y（n）间的时间延迟.令s（n）＝a（n）ej（ωcn＋φ（n）），其中a（n）为s（n）的包络，ωc为载频，φ（n）为s（n）的相位.重写式（1）为

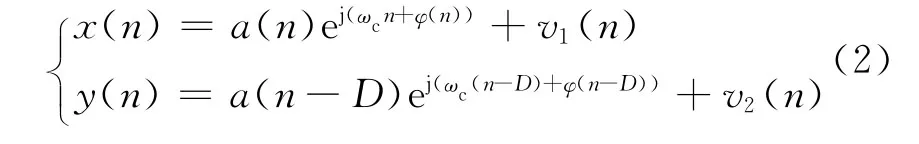
考虑到射频信号中心频率的分布特点，这里需要对信号进行中频变换处理.令ω0为接收机的本振频率，Δω为两接收机的本振频率差，则经中频变换后可得

观察式（3）可得

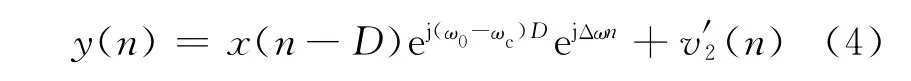
其中ej（ω0－ωc）D为一常数，记作α.于是当频差存在时两接收信号模型可以简化为

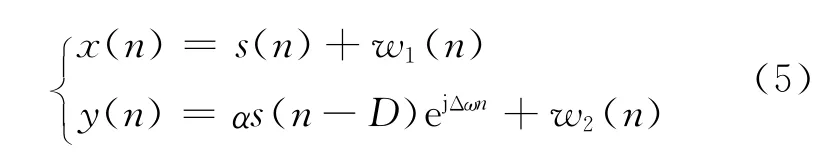
其中w1（n）和w2（n）仍为加性独立高斯白噪声，且与源信号互不相关.

当频差不存在即Δω＝0时，信号x（n）与y（n）的互相关函数为Rxy（m）＝Rss（m－D）.由离散傅里叶变换可得x（n）与y（n）的互功率谱密度函数为

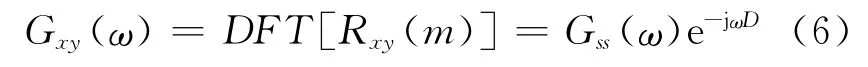
其中Gss（ω）为源信号s（n）的自功率谱密度函数，为实数.显然，时间延迟D体现在Gxy（ω）的相位函数上：

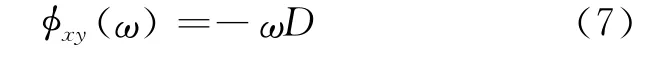
通过求解xy（ω）的斜率，即可得到时延估计值.

相位谱时延估计法的优点从式（7）可以看出，即两路信号的相位谱变化规律呈线性，如果将相位值看作一个随机过程的状态，那么如果已知状态转移矩阵，就可以利用Kalman滤波器对信号的相位谱进行线性拟合，改善信噪比，提高时延估计的精度.

但是，当频差Δω≠0时，观察式（3）可知已无法从相位函数中提取原始信号之间的时延信息D，这正是相位谱时延估计法的局限性之一；对于射频窄带信号来说，采用相位谱时延估计法的另一个局限性在于利用频域进行时延估计的有效点数受信号带宽的制约.

针对以上两点局限性，本文采用频差补偿的方法来解决中频偏差问题，采用CZT变换增加频域内进行时延估计的有效点数.

1.2 频差补偿的方法

由式（5）可知，通过对两路信号中频偏差的准确估计可提高对单路信号的频差补偿：

问题的关键就是如何估计两路信号的中频偏差Δω.一种方法是通过Hilbert变换[9]提取信号的包络进行时延估计，可以避免中频偏差的影响.但信号经过Hilbert变换后转变为基带信号，此时信号带宽减小为原来的1/2，则可利用的时延估计有效点数也随之减半，这样对时延估计精度的影响是很大的.本文采用一种更直接的方法，即利用平方倍频法首先估计出两路信号的中频后相减，然后按照式（8）直接对单路信号进行频差补偿.

平方倍频法原理如图1所示，以其中一路接收信号x（n）为例，为了方便推导，将式（3）中的x（n）写成实信号的形式，即

式中：x（n）为AM抑制载波信号，由于接收信号x（n）不含载波分量，a（n）中也没有直流分量存在，这样就不能将中频ω0直接过滤掉.x（n）经过平方器后输出为

其中p（n）表示为平方器的输出噪声.尽管a（n）中不存在直流分量，但经平方运算后a2（n）中却包含了直流分量，且式（10）中等式右端含有2ω0频率分量，可利用带通滤波器直接将其滤出，再通过二分频处理得到所需中频ω0.将估计出的两路信号中频做差，就可以得到中频偏差Δω.

图1 平方倍频法原理Fig.1 Principle of frequency doubling method

1.3 基于CZT的频域细化法

采用相位谱法对射频窄带源信号进行时延估计时，由于频域带宽的限制，可用于时延估计的有效点数较少，所含信息量有限.为了增加有效点数，本文采用CZT代替式（6）中的DFT，即

由于CZT不受频率分辨率的限制，能计算单位圆上任意一段曲线的Z变换，并且也可以依据特定需要确定均匀采样的间隔，更适合对特定窄带频谱进行细化与分析，具体原理介绍如下.

设序列x（n）的长度为N，其CZT定义[10]如下：

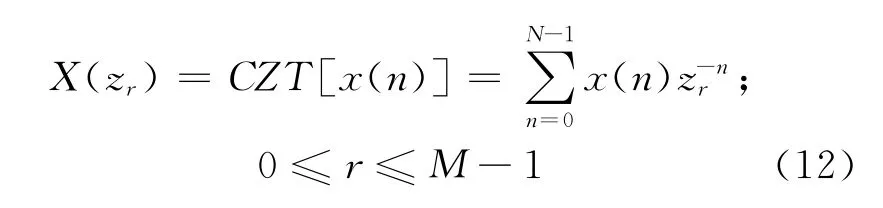
本文所研究的射频窄带信号的带宽一般在10kHz以下，以采样频率为50MHz、长度为106的射频窄带信号为例，该信号在频域内可用来计算时延估计的有效点数为

式中：B表示信号带宽，fs表示采样频率，N表示信号长度.显然仅利用这200个采样点进行基本的最小二乘相位谱时延估计很难达到较高的精度.

考虑单位圆上的CZT，此时A0＝W0＝1，在[2π（fc－B/2），2π（fc＋B/2）]弧度范围内对频谱进行2倍细化，即M＝2N，其中fc为载频，则可用来计算时延估计的有效点数为

显然NCZT＝2NDFT，即可用来计算时延估计的有效点数增加了1倍.

1.4 Kalman滤波器的设计

在使用相位谱法进行时延估计时，时延估计的精度受噪声的影响是不容忽视的，因此减小噪声的影响是非常必要的.Kalman滤波法是一种最优自回归数据处理方法，具有良好的抗噪声性能以及快速收敛特性[11、12].同时，采用相位谱时延估计法易于建立简单的Kalman模型来对信号的相位谱进行线性拟合，模型的状态方程和观测方程如下：

式中：xk为k时刻的状态向量，定义如下：

其中φk表示相位，φ′k表示斜率，是对相位取导数，即想求得的时延.A和H分别表示状态转移矩阵和观测矩阵，定义如下：

zk为k时刻的观测向量；wk－1和vk分别表示过程噪声和观测噪声，两者相互独立且均为零均值高斯白噪声，即

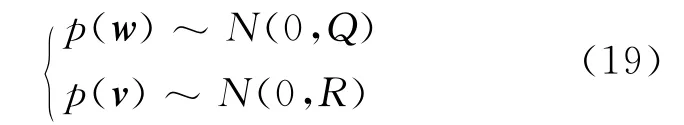
其中Q和R分别为过程噪声和观测噪声的协方差.

1.5 本文方法步骤

（1）首先采用平方倍频法分别估计出两路接收信号的中频ω01和ω02，相减得到两路信号的中频偏差Δω＝ω02－ω01.

（2）对单路信号按照式（8）进行频差补偿，消除中频偏差对时延估计的影响.

（3）用线性调频Z变换代替离散傅里叶变换，即利用式（11）求得信号的互功率谱密度，从而求得相位函数xy（ω）.

（4）利用本文设计的滤波器模型对相位函数xy（ω）进行线性拟合，求出xk中的斜率φ′k，即求得了所要的时延信息D.

方法步骤示意图如图2所示.

图2 本文方法示意图Fig.2 Schematic diagram of this paper′s method

2 仿真实验与结果讨论

总体仿真条件如下：设有用信号和噪声均服从均值为0，方差为1的高斯分布，且信号与噪声之间互不相关.调制信号为载波频率为10.7 MHz，采样频率为50MHz的AM抑制载波，选取数据长度为106，设时间延迟的真值为2μs.调制信号的带宽由10kHz递减到2kHz，信噪比由10dB递减到5dB，中频偏差由0.5kHz递增到2.5kHz，每种条件独立仿真100次，以100次时延估计的均方根误差作为衡量算法精度的指标，定义均方根误差如下式所示：

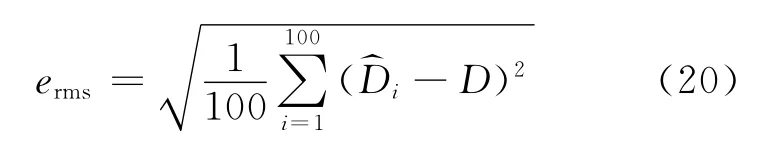
仿真实验中为了加快算法的运行速度，在用CZT求取两路信号的互功率谱过程中，选取输入点数的2倍作为输出点数，即M＝2N.为了加快算法迭代速度并得到更准确的迭代结果，在Kalman滤波的初值选取上，利用最小二乘法估计出相位和斜率的值作为状态向量的迭代初值，取预先多次实验仿真的均值作为观测噪声的协方差值.

本文对基于Hilbert变换取包络的最小二乘相位谱时延估计法（HLSP），基于Hilbert变换取包络及Kalman滤波的相位谱时延估计法（HKP），基 于 Hilbert变 换 取 包 络、CZT 及Kalman滤波的相位谱时延估计法（HCKP），基于频差补偿的最小二乘相位谱时延估计法（BLSP），基于频差补偿及Kalman滤波的相位谱时延估计法（BKP），本文提出的基于频差补偿、CZT及Kalman滤波的相位谱时延估计法（BCKP）分别进行了独立仿真实验.仿真实验结果比较如表1～3所示.

仿真结果表明：本文方法（BCKP）的时延估计精度明显优于其他5种方法，具有显著的优势.从表1可以看出：BCKP的精度高于HCKP，BKP的精度高于HKP，BLSP的精度高于HLSP，本文算法的均方根误差最小且稳定控制在30ns以内，由此可以得出，在克服中频偏差方面，直接进行频差补偿的方法要好于利用Hilbert取包络的方法.从表2可以看出：HCKP的精度高于HKP，BCKP的精度高于BKP，即使在带宽降到3kHz时，本文方法的均方根误差仍小于100ns，由此可以得出，在有限带宽内，利用CZT能更好地抑制窄带信号带宽的影响，提高时延估计的精度.从表3可以看出：表中前4种方法的精度明显高于后两种，其中本文方法（BCKP）的精度最高，由此可以得出，Kalman滤波器在改善信噪比方面具有良好的抗噪声性能.仿真分析表明，即使存在中频偏差，本文所提出的时延估计新方法仍能够得到较高精度.

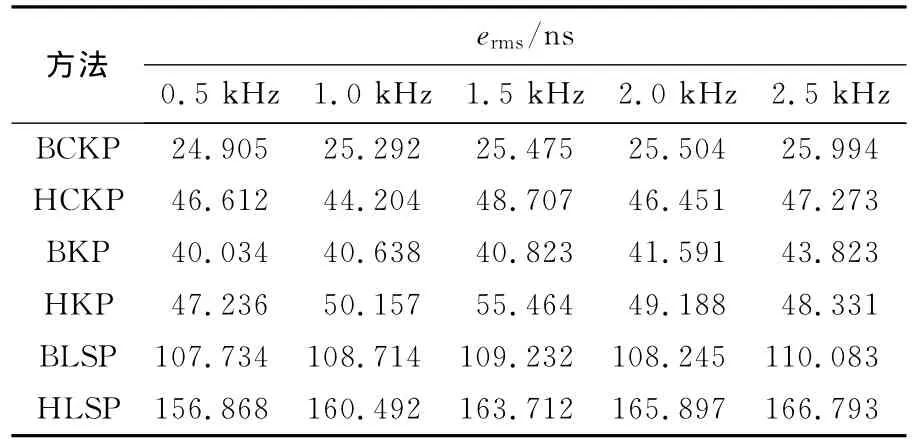
表1 调制信号带宽10kHz，信噪比10dB，6种方法在不同中频偏差下的ermsTab.1 ermscorresponding to different intermediate frequency difference of six methods（bandwidth is 10kHz，SNR is 10dB）

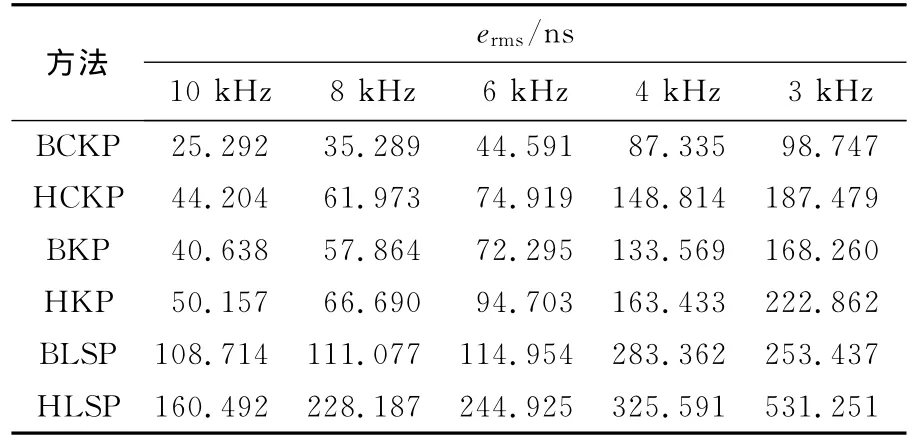
表2 信噪比10dB，中频偏差1kHz，6种方法在不同调制信号带宽下的ermsTab.2 ermscorresponding to different bandwidth of six methods （SNR is 10dB，intermediate frequency difference is 1kHz）

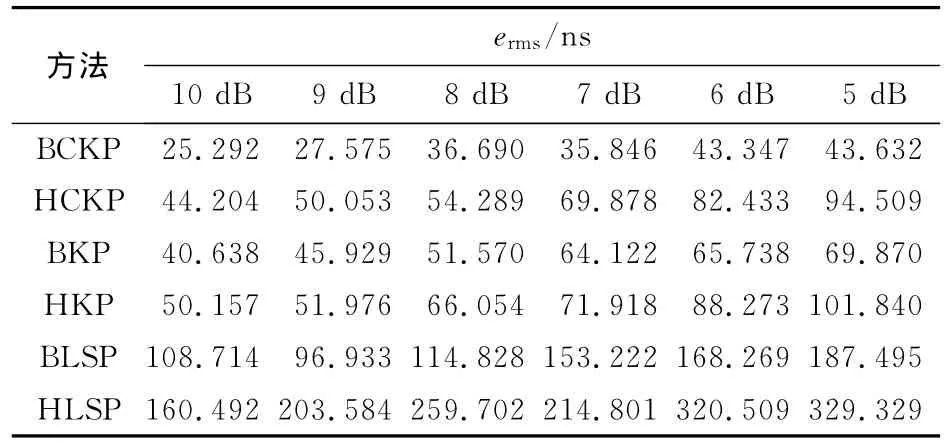
表3 调制信号带宽10kHz，中频偏差1kHz，6种方法在不同信噪比下的ermsTab.3 ermscorresponding to different SNR of six methods （bandwidth is 10kHz，intermediate frequency difference is 1kHz）

3 结 论

本文研究了存在中频偏差下射频窄带信号的时延估计问题，提出了一种基于频差补偿的相位谱时延估计新方法.该方法利用频差补偿的原理消除了由于两台接收机本振频率不一致而对后续时延估计产生的影响；针对窄带信号带宽较小的问题，利用CZT来增加相位法在有限带宽内可用于估计时延的有效点数；同时应用Kalman滤波器对相位谱进行线性拟合，改善信噪比.仿真实验结果表明，在中频偏差存在的条件下，本文方法能够对射频窄带信号进行较高精度的时延估计.

[1] KNAPP C H，CARTER G C.The generalized correlation method for estimation of time delay [J].IEEE Transactions on Acoustics，Speech，and Signal Processing，1976，24（4）：320－327

[2] 王 江，杨景曙.频差存在时广义相关时延估计方法研究[J].信号处理，2008，24（1）：112－114

[3] PIERSOL A G.Time delay estimation using phase data[J].IEEE Transactions on Acoustics，Speech，and Signal Processing，1981，29（3）：471－477

[4] VIOLA F，WALKER W F.A comparison between spline－based and phase－domain time－delay estimators[J].IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2006，53（3）：515－517

[5] ZHENG C，TJENG T T.A new time delay estimator based on ETDE [J].IEEE Transactions on Signal Processing，2003，51（7）：1859－1869

[6] 王宏禹，邱天爽.自适应噪声抵消与时间延迟估计[M].大连：大连理工大学出版社，1999：170－285

[7] SHARMA K K，JOSHI S D.Time delay estimation using fractional Fourier transform [J]. Signal Processing，2007，87（5）：853－865

[8] 郭 莹，邱天爽，张艳丽，等.脉冲噪声环境下基于分数低阶循环相关的自适应时延估计方法[J].通信学报，2007，28（3）：8－14

[9] CABOT R.A note on the application of the Hilbert transform to time delay estimation [J].IEEE Transactions on Acoustics， Speech， and Signal Processing，1981，29（3）：607－609

[10] 郭 莹，邱天爽，张艳丽.基于共变谱的CZT多源时延估计新方法[J].大连理工大学学报，2007，47（5）：746－750（GUO Ying，QIU Tian－shuang，ZHANG Yan－li.A novel multi－source time delay estimation method based on CZT and covariation spectrum [J].Journal of Dalian University of Technology，2007，47（5）：746－750）

[11] KALMAN R E.A new approach to linear filtering and prediction problems [J].Transactions of the ASME — Journal of Basic Engineering，1960，82（Series D）：35－45

[12] SHAW S R，LAUGHMAN C R.A Kalman－filter spectral envelope preprocessor [J]. IEEE Transactions on Instrumentation and Measurement，2007，56（5）：2010－2017