时域间断Galerkin有限元法在激光热加工过程中应用

吴 志 刚， 郭 攀， 武 文 华＊

（1.大连理工大学 航空航天学院，辽宁 大连 116024；2.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024）

0 引 言

在工程实际中，由于激光的定向性、单色性好，发散角小的特点，激光技术具有很好的局部性以及能量的精确性.目前，激光热加工、热处理技术已经得到了广泛应用.当利用激光束加热固体介质时，在介质表面和内部出现光波吸收、反射、折射的效应，但其中大部分自由电子的能量通过电子与晶格或离子的相互作用转化为介质热能并进行热扩散，引起固体介质内部不同程度的温度上升[1].常规条件下，介质内部的温度场可以通过经典的傅里叶定律理论进行描述.但随着超短脉冲激光、激光作用下金属快速凝固等技术的应用，经典傅里叶定律存在着明显的缺陷，热传导中非傅里叶效应的影响得到人们的重视[2].傅里叶定律理论认为热流与温度梯度成正比，温度场可以由抛物线型热传导方程来描述.但当热作用瞬时时间达到皮秒级、飞秒级，热扩散的速度就有了奇异性.就必须要考虑介质热传导过程中的松弛行为，即热流矢量和温度梯度间存在了时间延迟.现在，已经有大量数学模型对这种现象进行描述.如单相延迟模型、双向延迟模型、微观两步模型、纯声子散射模型等[3、4].其中单相延迟双曲型热传导模型在工程中应用得最为广泛.

目前主要使用差分法、有限元法等数值方法进行考虑非傅里叶效应的数值模拟.在时域处理上往往利用差分法对问题进行求解.为了避免数值振荡，时域差分法对时间步长的要求非常严格[5].本文应用时域间断Galerkin有限元法针对受激光热源作用的半无限体和薄膜温度场分布问题进行求解，并使用算例对结果进行验证.

1 单相延迟双曲型热传导模型与时域间断Galerkin方法

单相延迟双曲型热传导模型中与时间相关的函数为

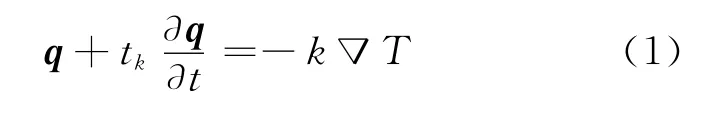
式中：q为热流矢量，tk为松弛时间，k是导热系数，T是温度[6].

考虑瞬态能量守恒方程：

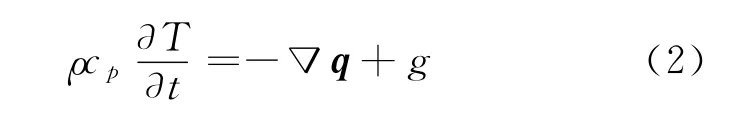
式中：ρ是介质密度，cp是定压比热容，g是所施加的激光热源.其函数形式为

式中：I（t）是激光热源强度，R为介质表面反射率，μ是介质吸收系数.将式（2）、（3）代入式（1）中，得到双曲型激光热传导方程：

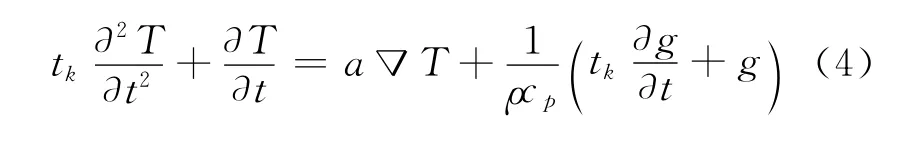
式中：a是热扩散系数是热波动速度.

对上式进行量纲一化处理，表达式如下：

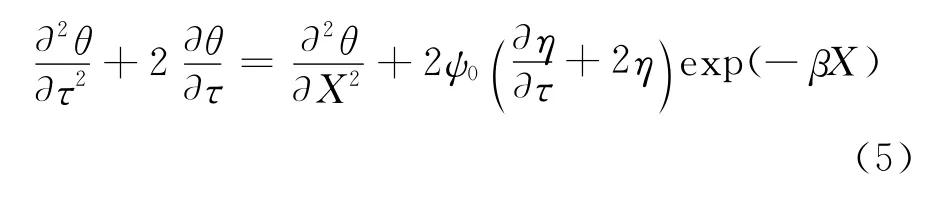
式中：θ是量纲一温度，τ是量纲一时间，X是量纲一长度，ψ0是量纲一内热源系数，η是量纲一热源，β是量纲一热吸收系数.

半无限问题和薄膜问题相应的量纲一化后初始条件表示如下：

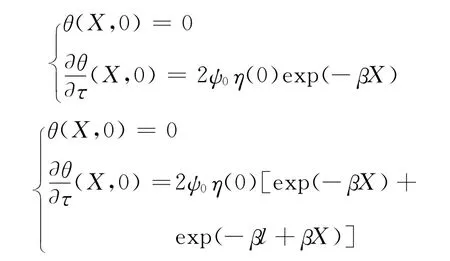
时域间断 Galerkin方法[7、8]是在传统的空间域有限元方法分析基础上，区别于习惯对时域（0，T）利用连续差分法求解，对时域进行有限元间断插值离散.

双曲型热传导方程空间域离散得

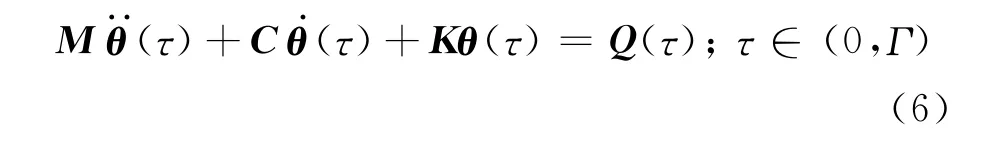
其中

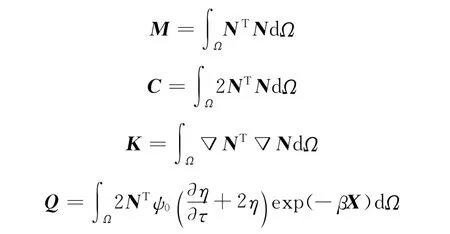
时域离散可表示为

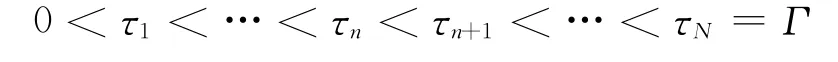
时域离散时允许基本未知函数θ与其导数ν在离散点处间断.即在时刻τn的未知函数值表示为

在任意时间步In＝ （τn，τn＋1）内，对时域基本未知函数θ采用三次Hermite插值，对时域基本未知函数导数ν和热源Q采用线性插值.

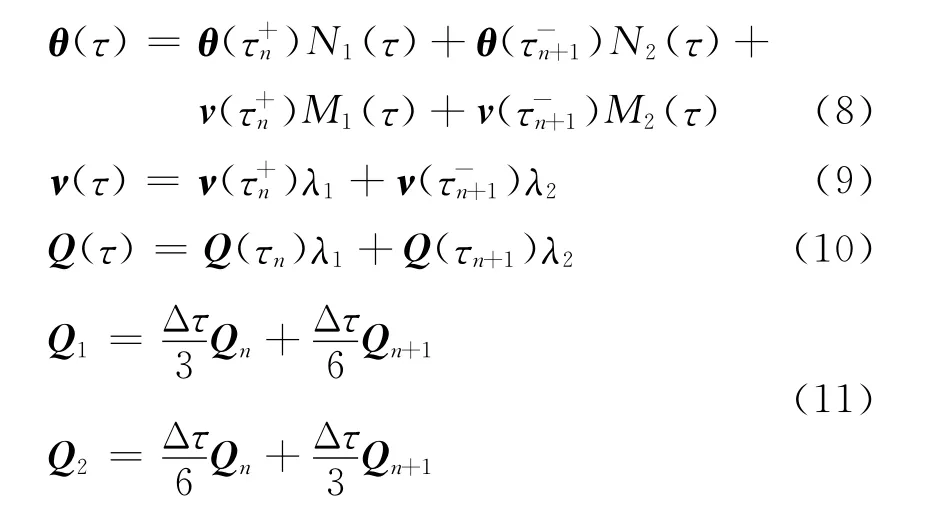
对温度函数θ与其导数ν作为独立的变量进行变分，利用式（6）、（7）并选取控制条件θ·－ν＝0构造典型的间断Galerkin有限元法的弱形式，表示为

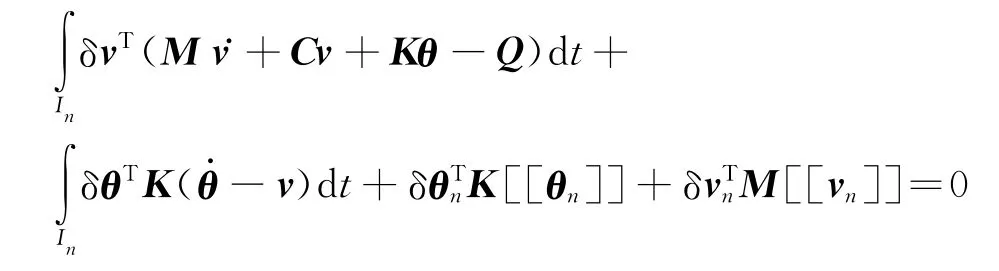
把式（8）～（11）代入上式，可以进一步转化为解耦的式（12），即时域间断Galerkin有限元法的基本求解公式.从式中不难发现温度向量在时域内间断点处不再存在间断，仅保留温度时间导数在时间间断点处存在间断，大大减少了基本未知数的个数，节省了求解时间.

第n＋1时刻的温度为

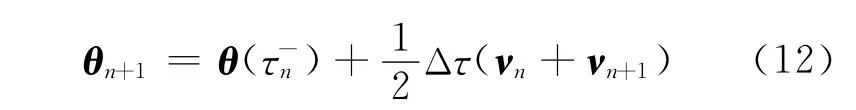
2 算例和结果

本文选取工程中常用的几类激光热源η形式（式（13）～（15）），利用时域间断 Galerkin有限元法分别对半无限体一端和薄膜两端受激光热源作用进行数值分析.

3类热源表达式如下：

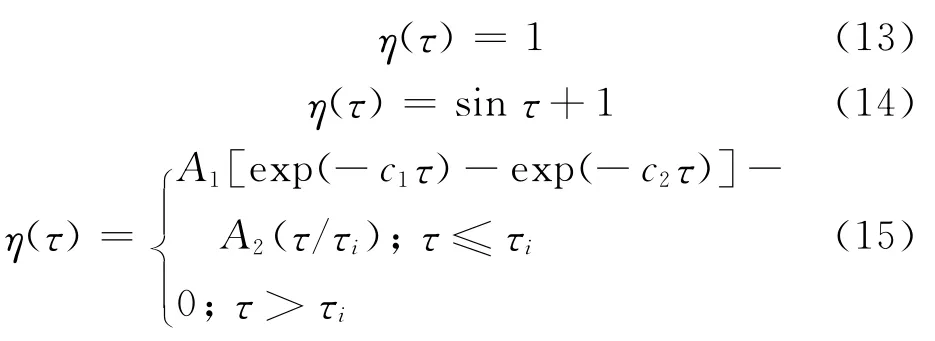
算例1 考虑一个半无限体的一维问题，如图1所示[4、9].半无限体左端分别受式（13）～（15）的3类激光热源作用，初始条件为

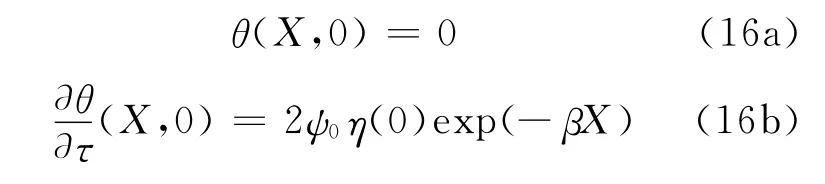
假定ψ0＝1，β＝1.

图1 半无限体左侧受激光热源作用模型Fig.1 Model of semi－infinite body subjected to laser heat source in its left side

在计算中，选取一维单元进行分析，单元长度为0.05，单元数为200，节点数为201，时间步长为0.000 75.

首先考虑热源为式（13）时的数值模拟，可求得沿轴方向上在1、3、6、9s时温度分布，如图2所示.同时给出数值解与解析解对比，其良好的吻合程度显示出计算结果的可靠性.

然后考虑第二类激光热源（式（14）），选取矩形四节点单元作为分析对象，单元的尺寸为0.05×1，单元数为600，节点数为804，时间步长为0.05.与第一类激光热源作用选取的时间步长相比，第二类激光热源作用所选取的时间步长明显增大.当热源满足式（14）时x、y长度方向上温度分布如图3所示.

为了验证方法的适用性，在式（15）作为激光热源的工况下，选取3种不同尺寸的矩形四节点单元进行计算.三类单元尺寸分别为0.05×1、0.02×1、0.01×1，如图4所示.单元数为450，节点数为604，时间步长为0.05.可以求得x、y长度方向上温度分布如图5所示.需要说明的是，在第二和第三类激光热源的工况下，也进行了一维单元的计算，其计算结果与二维计算结果相同.

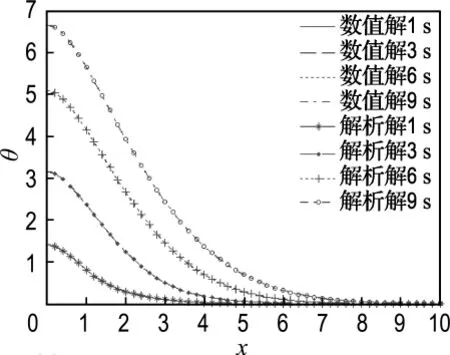
图2 算例1第一类激光热源在1、3、6、9s时温度分布Fig.2 Temperature distributions at 1，3，6，9 second under 1st type of laser heat source in the first example

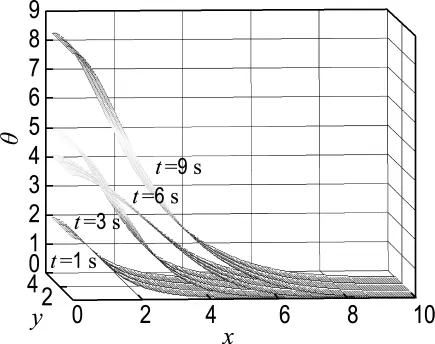
图3 算例1第二类激光热源1、3、6、9s时温度分布Fig.3 Temperature distributions at 1，3，6，9 second under 2nd type of laser heat source in the first example

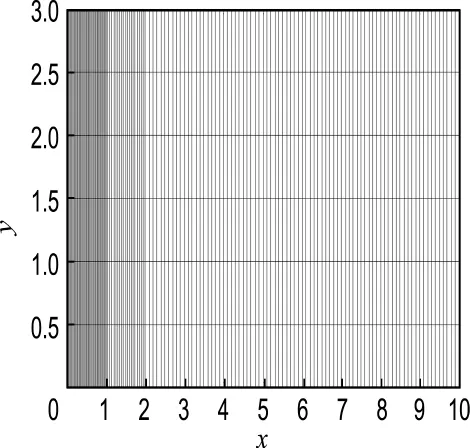
图4 算例1第三类激光热源计算构型的网格划分Fig.4 Computational configuration in 3rd laser heat source in the first example

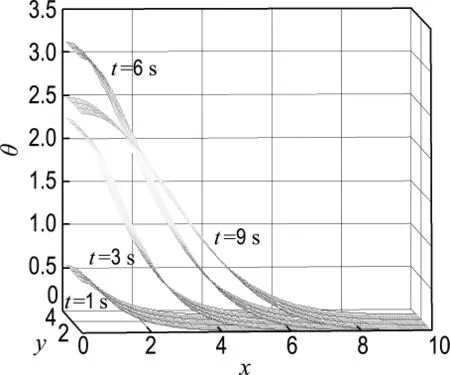
图5 算例1第三类激光热源在1、3、6、9s时温度分布Fig.5 Temperature distributions at 1，3，6，9 second under 3rdtype of laser heat source in the first example

算例2 激光加热薄膜过程中，薄膜内将产生能量沉积，光能转化为热能，从而导致薄膜破坏.本算例考虑薄膜两端都受有激光热源作用的热传导问题[1、9].模型如图6所示，与算例1类似，薄膜两端分别考虑3类不同的激光热源作用，同时假定薄膜两端的初始条件和边界条件对称，即初始条件分别如下：

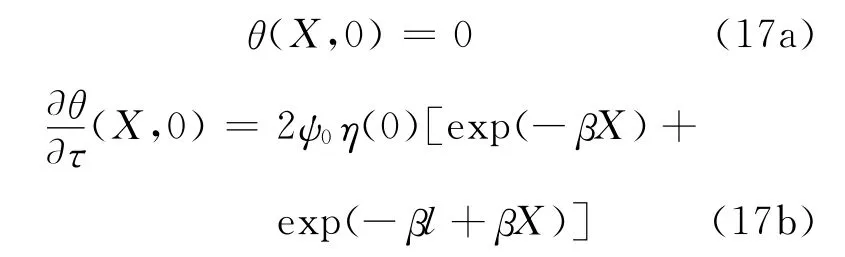
并考虑ψ0＝1，β＝1.

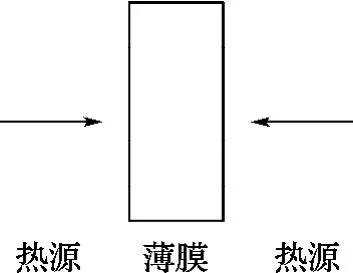
图6 薄膜激光热源模型Fig.6 Model of thin film with laser heat source

在计算中，全部选取一维单元，单元长度为0.05，单元数为200，节点数为201，时间步长为0.000 75，薄膜厚度为10个单位.

当热源满足式（13）时求得薄膜长度方向的温度分布如图7所示.

当热源满足式（14）时同样可以求得薄膜长度方向的温度分布如图8所示.

当热源满足式（15）时可以求得薄膜长度方向的温度分布如图9所示.

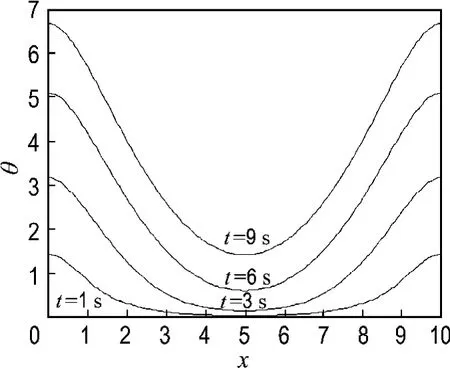
图7 算例2第一类激光热源下1、3、6、9 s时温度分布Fig.7 Temperature distributions at 1，3，6，9 second under 1st type of laser heat source in the second example

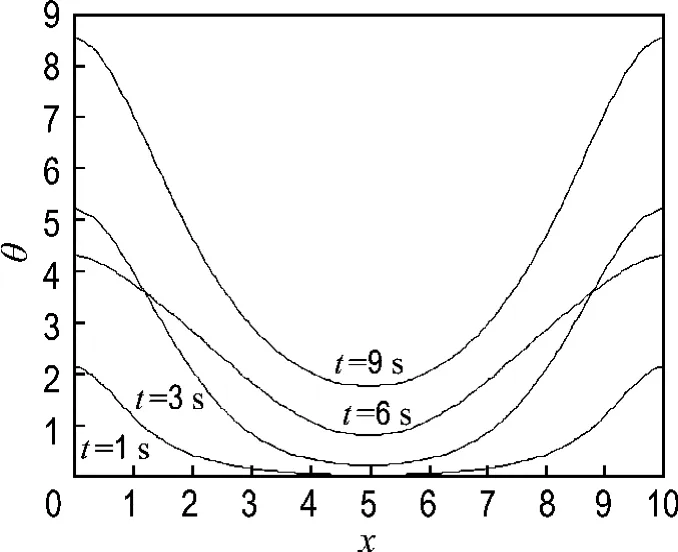
图8 算例2第二类激光热源下1、3、6、9s时温度分布Fig.8 Temperature distributions at 1，3，6，9 second under 2ndtype of laser heat source in the second example

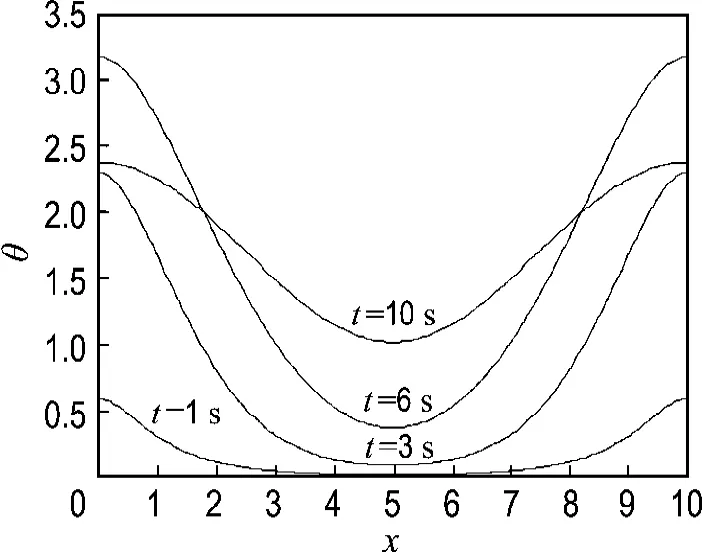
图9 算例2第三类激光热源下1、3、6、10s时温度分布Fig.9 Temperature distributions at 1，3，6，10 second under 3rd type of laser heat source in the second example

将计算结果与文献[9、10]相比，可以看出利用时域间断Galerkin有限元法所得到的计算结果与解析解十分吻合.

3 结 语

本文利用时域间断Galerkin有限元法对单相延迟的双曲型激光热源作用的热传导过程进行了数值模拟，分别考虑了半无限体和薄膜两种情况下的热传导过程.

计算结果显示出，由于时域间断Galerkin有限元法在时域上对时间函数及其导数进行了一阶到三阶的插值，并且允许时间函数和其导数在时间节点上间断，保证了时间函数连续的同时，有效避免了在计算激光热传导时对时间函数进行差分而带来的数值振荡现象.时域间断Galerkin有限元法是分析瞬态激光非傅里叶热传导问题的有效方法.

[1] 孙承伟.激光辐照效应[M].北京：国防工业出版社，2002

[2] 刘 静.微米/纳米尺度传热学[M].北京：科学出版社，2001

[3] 蒋方明，刘登瀛.非傅立叶导热的最新研究进展[J].力学进展，2002，32（1）：128－140

[4] M.VON奥尔曼.激光束与材料相互作用的物理原理及应用[M].北京：科学出版社，1994

[5] 孔祥谦.热应力有限元法分析[M].上海：上海交通大学出版社，1999

[6] TAMMA K K，NAMBURU R R.Computational approaches with applications to non－classical and classical thermo mechanical problems [J].Applied Mechanics Reviews，1997，50（9）：514－551

[7] 李锡夔，姚冬梅.弹塑性体中波传播问题的间断Galerkin有限元方法[J].固体力学学报，2003，24（24）：399－409

[8] 武文华，李锡夔.固体非傅里叶温度场的间断Galerkin有限元方法[J].计算力学学报，2007，24（2）：219－223

[9] LEWANDOWSKA M.Hyperbolic heat conduction in the semi－infinite body with a time dependent laser heat source [J].Heat and Mass Transfer，2001，37（4－5）：333－342

[10] SHUICHI Torii，YANG Wen－jie. Heat transfer mechanisms in thin film with laser heat source[J].Heat and Mass Transfer，2005，48（3－4）：537－544