基于最小二乘支持向量机动态逆的非线性系统自适应控制

谢 春 利， 邵 诚， 赵 丹 丹

（1.大连理工大学 电子信息与电气工程学部，辽宁 大连 116024；2.大连民族学院 机电信息工程学院，辽宁 大连 116600；3.大连民族学院 计算机科学与工程学院，辽宁 大连 116600）

0 引 言

动态逆[1]方法是一种行之有效的非线性系统控制方法.但是常规的逆系统方法要求受控对象有精确数学模型，这对于大多数工业过程难以做到，即使建立起非线性动力学模型，一般也难以求得逆模型的解析形式.由于神经网络具有对任意非线性动态特性逼近的能力，有些学者[2、3]提出了基于神经网络动态逆的非线性系统自适应控制方法，得到了很好的应用效果.其基本思想是，利用离线神经网络辨识受控对象的动态逆模型，同时通过在线神经网络自适应地补偿系统的动态逆误差.但是神经网络算法存在局部最小点、结构设计困难、过学习现象及收敛速度慢等缺点，使其应用具有一定的局限性.

最小二乘支持向量机（least squares support vector machines，LS－SVM）[4～6]是近十年来机器学习领域的一个重要成果，它把标准支持向量机训练中的二次规划问题转化为解线性方程组问题，极大地提高了训练效率.此外，它保持了标准支持向量机的强大泛化和全局最优能力，因此LS－SVM能够克服神经网络的固有缺陷.目前，利用LS－SVM对未知非线性动态特性进行逆建模的控制方案有了许多成功的应用[7～14].但是，这些方法没有考虑到动态逆误差的影响，同时也不能保证闭环系统的稳定性.

本文提出基于LS－SVM动态逆的非线性系统自适应控制方法，该方法采用离线LS－SVM辨识非线性系统的动态逆模型，并将其应用于非线性动态系统的直接逆模控制.为克服基于输入输出数据辨识动态逆模型不精确引起的建模误差，采用在线LS－SVM进行自适应补偿，并对LSSVM方法和神经网络方法的仿真结果进行比较.

1 最小二乘支持向量机回归

设样本数据D＝｛（xk，yk）｜k＝1，2，…，N｝，xk∈Rn为输入数据，yk∈R为输出数据，LS－SVM回归模型的目标就是构造一个如下所示模型：

使得样本x对应的函数值yk能用y（x）近似.这里非线性映射φ（x）把输入数据映射到一个高维特征空间.LS－SVM回归算法就是要求解下面的优化问题：

式中：J为优化目标函数，w∈Rnh为权矢量，γ∈R为正则化参数，εk∈R为不敏感损失函数的松弛因子，φ（·）：Rn→Rnh为核空间映射函数，b∈R为偏移量.其对偶问题的拉格朗日多项式为

其中拉格朗日乘子αk∈R.通过L对w、εk、b和αk求偏导等于零，可得

消除变量w和εk，可得此优化问题的解析解为

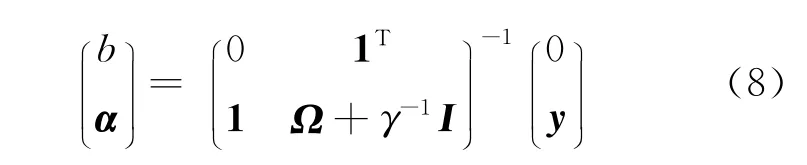
式 中：y＝ （y1y2…yN）T∈RN；1 ＝（1 1 … 1）T∈RN；α＝（α1α2…αN）T∈RN；I∈RN×N是单位方阵；Ω∈RN×N为方阵，其第k行l列 的 元 素 为Ωkl＝K（xk，xl） ＝φT（xk）φ（xl），k，l＝1，2，…，N.

K（·，·）为核函数，它为满足 Mercer条件[15]的任意对称函数.核函数常使用下面3种：

（1）线性核函数

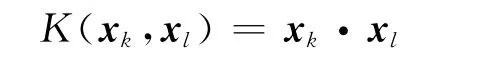
（2）多项式核函数

（3）高斯径向基核函数

其中d为多项式的阶次，σ为核宽度.本文综合考虑计算效率和逼近精度，选取高斯径向基核函数.

通过计算式（8）解得α和b，并进一步计算求得w，最终得到LS－SVM的函数逼近为

参数γ和σ的取值对LS－SVM的函数逼近效果影响较大，因此，本文采用交叉验证方法对参数进行优化选取.

2 非线性系统直接自适应逆控制

对于如下状态可观测的非线性系统

式中：x为系统的状态量，u为系统的控制量，y为系统的输出量，x∈Rn，u∈Rl，y∈Rm.f（·，·）是未知的非线性函数，C为适维矩阵.系统控制方案如图1所示.

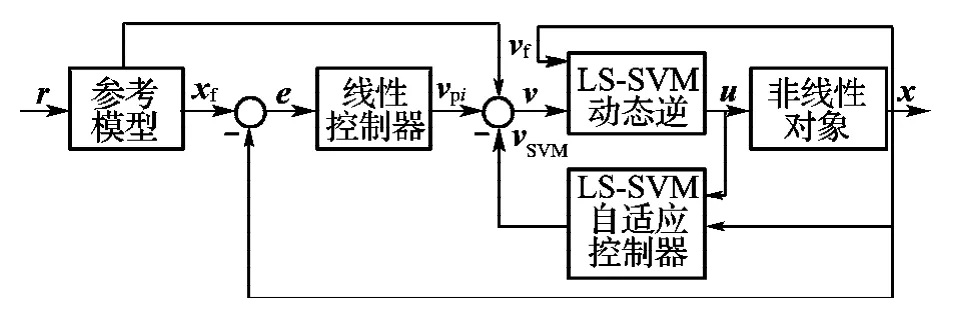
图1 基于最小二乘支持向量机动态逆的自适应控制Fig.1 Self－adaptive control based on LS－SVM dynamic inversion

该方案中的动态逆由LS－SVM来实现并与原系统复合成伪线性系统；参考模型和线性控制器按期望的系统性能进行设计；LS－SVM自适应控制器用来补偿逆误差.控制的目标是设计控制律u使得闭环系统稳定，且状态x跟踪参考模型状态xf.

2.1 基于最小二乘支持向量机的动态逆控制器设计

如果f（x，u）是可逆的，x是可测的，基于逆系统方法，引入伪控制量v，伪控制量和状态量之间为线性关系：

其中

控制输入通过计算下式得到：

在传统的LS－SVM建模中，输出都是一维的，因此许多文献通常都是针对单输出的情况.但是，当非线性系统模型为多输入多输出时，系统输入输出之间往往存在耦合，而它们的解耦通常非常困难.本章通过考虑输入输出量之间的耦合作用，根据样本数据对每个控制通道分别应用LS－SVM进行直接逆建模，然后将各通道分量输出集成为控制向量u.采用该建模方法，构成每个通道分量模型的支持向量和权值向量是不尽相同的，后面在具体描述时，通过下标进行区别.

动态逆误差由求逆建模误差和外界干扰等引起.考虑逆误差的存在，系统的动态方程可以表示为

式中：Δinv为采用近似f而产生的系统逆误差，由式（14）可知，逆误差可以看作状态量和控制量的非线性时变函数，表示为

由伪控制量和动态逆误差的定义，系统方程可等价表示为

逆误差的存在会导致非线性系统的控制效果急剧恶化.本文在LS－SVM 动态逆控制中引入由LS－SVM构造的自适应控制器，其输出信号与伪控制量叠加，抵消动态逆误差的影响，控制系统结构如图1所示.

图1中，r∈Rn为参考模型的输入，xf∈Rn为参考模型的状态信号，对于式（10）描述的系统，参考模型可以表示为

参考模型输出的伪控制信号为

式中：ff为参考模型的系统模型参考模型引出的信号.

线性控制器按照常规PI控制器设计.对于状态向量中的每个分量，第k个线性控制器输出的控制分量为

其中Kpk、Kik分别为比例、积分增益.

伪控制向量的每个分量由参考模型输出的分量、比例积分控制分量和LS－SVM自适应补偿器输出分量3部分构成：

式中：vSVMk为LS－SVM自适应控制器输出分量，用于补偿动态逆误差.将式（20）代入式（16），可以将每个跟踪误差分量动态特性写为如下形式：

其中

选择Kpk、Kik确保系统矩阵Ak为霍尔维茨矩阵.由式（21）可知，在理想情况下自适应控制器输出能够抵消系统逆误差，系统跟踪误差稳定收敛于零.

2.2 自适应最小二乘支持向量机的构造

采用LS－SVM在线补偿动态逆误差，其思想就是在控制中，不断地测量误差信号，并用LSSVM去逼近这个信号，然后把LS－SVM的输出引入伪线性系统的控制输入，在线消除系统的近似逆误差和LS－SVM的逼近误差，使系统性能得到改善.第k个LS－SVM自适应补偿器的结构如图2所示.

图2 最小二乘支持向量机结构Fig.2 Structure of least squares support vector machines

于是vSVM向量中第k个分量的输入输出关系为

由LS－SVM的全局逼近能力[16]可知，只要参数选择合适，LS－SVM能够一致逼近任意连续非线性函数.因此对于不确定的非线性动态逆误差及任意给定的重构误差εk＞0，存在最优的权值向量分量使得

则式（21）变为

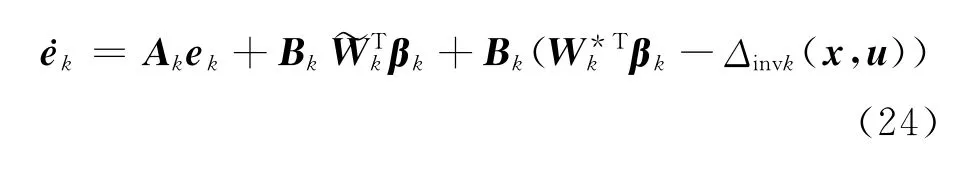
定理1 对于式（10）描述的系统，采用图1所示的自适应控制结构，其中第k个控制分量的解析表达为式（20），自适应控制器输出的第k个分量为式（22），如果选取其权值调整规律为

其中ηk＞0是自适应增益；Pk为正定对称矩阵，满足

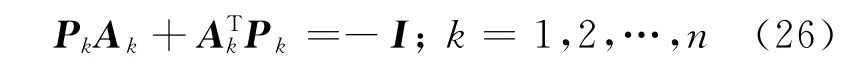
则闭环系统内所有信号保持有界.

证明 选择如下Lyapunov函数：

其中

只要矩阵Ak为霍尔维茨矩阵，矩阵Pk一定存在.式（28）中的E0k选为[17]

由式（24）～ （26）可得

由式（23）有

采用式（25）自适应律可以得到

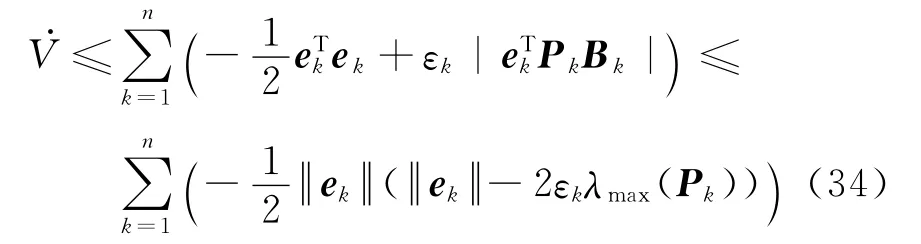
如果式（25）中的e0k满足

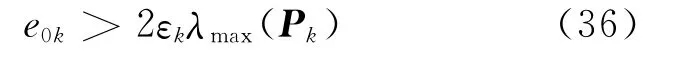
总之，Vk（k＝1，2，…，n）具有以下性质：

（1）Vk≥e0k＞0，且Vk是连续的；

基于LS－SVM动态逆的非线性系统自适应控制实现过程如下：

（1）根据非线性系统模型选取求逆模型，确定求逆模型的输入输出变量.

（2）施加均值0、方差0.01的白噪声信号，采样100组的输入输出训练数据，并等间隔取40组数据作为测试样本.对直接逆模型中的每个分量以最小化均方误差为目标，利用交叉验证方法优化得到LS－SVM的最优超参数.重新进行离线训练，得到LS－SVM的权值参数初值.

（3）投入运行直接动态逆控制器和线性控制器，采样输入向量与的状态偏差信号，对自适应LS－SVM补偿通道中每个分量进行超参数优化选择和求取支持向量.

（4）自适应LS－SVM补偿器投入在线使用，依据式（25）自适应调整权值.

3 仿真研究

考虑一个非线性系统

其中d（t）为有界干扰.设初始值x（t）＝0，令d（t）＝sint.选取Kp＝20，Ki＝20，解式（26）得

控制的目标是使输出y跟踪给定的单位阶跃信号1（t）.

分别采用LS－SVM和神经网络来构造动态逆控制器和自适应补偿器，研究非线性对象的控制效果.用于实现直接动态逆控制器的神经网络采用3－5－1结构，用于自适应补偿器的神经网络采用4－5－1结构.

由图3和4仿真结果可知，采用自适应补偿器极大地改进了系统的控制品质，表明本文提出的方法是有效的.同时，对比LS－SVM方法和神经网络方法的仿真结果可知，前一方法的控制精度更高.

图3 无自适应补偿器时，动态逆系统输出响应Fig.3 Output response of the dynamic inversion system without self－adaptive compensator

图4 有自适应补偿器时，动态逆系统输出响应Fig.4 Output response of the dynamic inversion system with self－adaptive compensator

4 结 论

本文针对一类未知且包含扰动的非线性系统，基于LS－SVM动态逆提出了一种新的自适应控制方案.该方案采用离线LS－SVM对系统中的未知非线性动态特性进行动态逆建模，构建复合的伪线性系统.对于动态逆建模和外界扰动等引起的系统误差，利用在线LS－SVM构建的自适应控制器进行补偿.基于Lyapunov理论建立了闭环系统的稳定性.仿真结果表明LS－SVM动态逆控制是一种有效的非线性控制策略.

[1] BRINKER J，WISE K.Stability and flying quality robustness of a dynamic inversion aircraft control law[J].Journal of Guidance，Control and Dynamics，1996，19（6）：1270－1278

[2] CALISE A J，RYSDYK R T.Nonlinear adaptive flight control using neural networks [J].IEEE Control Systems Magazine，1998，18（6）：14－25

[3] CALISE A J， HOVAKIMYAN N，IDAN M.Adaptive output feedback control of nonlinear systems using neural networks [J].Automatica，2001，37（8）：1201－1211

[4] SUYKENS J A K，VANDEWALLE J.Least squares support vector machine classifiers [J]. Neural Network Letters，1999，9（3）：293－300

[5] SUYKENS J A K.Nonlinear modeling and support vector machines[C]//Proceedings of the 18th IEEE on Instrumentation and Measurement Technology Conference.Budapest：IEEE Press，2001：287－294

[6] SUYKENS J A K.Support vector machines：a nonlinear modeling and control perspective [J].European Journal of Control，2001，7（2－3）：311－327

[7] 柳晓菁，易建强，赵东斌，等.基于最小二乘支持向量机的自适应逆扰动消除控制系统 [J].控制与决策，2005，20（8）：947－950

[8] SU S W，WANG L，CELLER B G，etal.Modelling and control for heart rate regulation during treadmill exercise[C]//Proceedings of the 28th IEEE EMBS Annual International Conference.New York：IEEE Press，2006：4299－4302

[9] 欧阳军，闫桂荣，王 腾.LS－SVM在随机振动在线自适应逆控制中的应用 [J].应用力学学报，2007，24（4）：531－534

[10] YUAN X F，WANG Y N.LS－SVM modeling based inverse controller with uncertainty compensation[J].Journal of Dynamic Systems，Measurement，and Control，2007，129（6）：845－850

[11] YUAN X F，WANG Y N，WU L H.Adaptive inverse control of excitation system with actuator uncertainty[J].WSEAS Transactions on Systems and Control，2007，2（8）：419－427

[12] 沈曙光，王广军，陈 红.最小支持向量机在系统逆动力学辨识与控制中的应用 [J].中国电机工程学报，2008，28（5）：96－101

[13] 程启明，杜许峰，郭瑞青，等.基于最小二乘支持向量机的多变量逆系统控制方法及应用 [J].中国电机工程学报，2008，28（5）：85－89

[14] 杨志峰，雷虎民，董飞垚，等.基于LS－SVM的导弹在线误差补偿逆控制 [J].系统工程与电子技术，2010，32（6）：1314－1317

[15] VAPNIK V.An overview of statistical learning theory[J].IEEE Transactions on Neural Networks，1999，10（5）：988－999

[16] GESTEL V T，SUYKENS J A K，BAESTAENS D E，etal.Financial time series prediction using least squares support vector machines within the evidence framework [J].IEEE Transactions on Neural Networks，2001，12（4）：809－821

[17] PETERSON B B，NARENDRA K S.Bounded error adaptive control [J]. IEEE Transactions on Automatic Control，1982，AC－27（6）：1161－1168