码分多址定位中时延配对及非视距误差抑制
邓冬虎 张 群 林永照 柏 鹏 高昭昭
(1.空军工程大学信息与导航学院,陕西 西安 710077; 2.空军工程大学综合电子信息系统研究中心,陕西 西安 710077; 3.信息综合控制重点实验室,四川 成都 610036)
引 言
无源定位是信号处理领域的一个重要研究方向[1]。随着民用移动通信的发展,基于移动通信信号的外辐射源雷达已成为当前研究的热点[2-3]。码分多址(CDMA)体制近年来取得了巨大的发展,已成为第三代移动通信标准的主流[2],在各国都得到了广泛应用。相关学者研究发现,CDMA蜂窝网具有良好的导频信号自相关特性和各基站同步工作等优点,为采用波达时间差(TDOA)定位创造了条件,展开面向CDMA蜂窝网的定位算法的研究具有重要的意义和应用前景[2,4]。但是,利用CDMA蜂窝导频信号实现对运动目标的定位也存在一些难点:
1) 时延参数的估计与配对问题。在估计时延参数时,通常采用检测该基站对应的模糊函数的峰值来得到其时延参数。但是,由于CDMA各基站的导频序列相差64个码片的整数倍,得到的既可能是该基站回波信号的时延,也可能是其他基站信号的时延。因此,如何实现各基站与时延参数的配对,成为一个需要解决的难题。虽然文献[4]结合基站与接收站之间的几何关系,提出了一种利用“簇”的算法来配对时延和基站。但是当电波在目标和小区基站之间存在非视距(NLOS)路径时[5],“簇”算法不再适用。为解决这一问题,提出了一种基于移位配准的配对方法,即构造关于峰值与各基站时延参数的映射函数,通过最大似然检测进行遍历,实现各基站与时延的配对。
2) TDOA定位中NLOS误差抑制问题。文献[6]将时延测量值通过设定的1-σ滤波器来估计测量误差,然后结合最小二乘算法得到目标位置。虽然计算方法简单,但是并没有对各基站的误差分别进行考虑,导致定位精度不高;文献[7]则利用基站与目标位置的几何图案关系来判定各基站是否为NLOS基站,实现对NLOS误差的抑制,但太过依赖于先验知识[8];文献[9-12]则采用残差函数来实现NLOS环境下目标的定位,虽然不需要过于依赖先验知识,但是没有对NLOS基站进行分类分析来提高定位精度。为了进一步提高NLOS环境下的TDOA定位性能,提出了一种基于假定NLOS基站的方差函数,并以此作为权值,利用加权平均的办法,对目标估计位置进行计算,来对目标定位。同时,对受到NLOS影响的基站进行检测,若检测到的NLOS基站数目较少,则结合泰勒(Taylor)级数展开算法,可获得更好的目标位置估计结果。
1 时延估计及与基站的配对
图1为利用CDMA基站发射的导频信号对运动目标进行探测和定位的系统示意图。从图中可以看出,接收站所接收到的信号包括各基站发射导频信号的目标回波信号和直达干扰分量,以及其他的多径干扰分量。为了准确估计出运动目标对应各基站信号的时延,就必须要消除接收信号中的干扰分量。因为接收信号中干扰分量的多普勒频移为零,而目标反射信号因为目标的运动会产生一定的多普勒频移,所以可以在多普勒域,利用级联对消的方法,消除干扰分量[4]。受于篇幅限制,假设所有干扰分量已经消除(关于干扰分量消除方法,有兴趣的读者可参阅文献[4]),接收站所接收到的信号只包括各基站所对应的目标回波信号和噪声。

图1 目标探测与定位系统示意图
由此可知,经混频、滤波后的接收信号为
(1)
式中:N为基站个数;xi(t)表示基站i发射的导频信号;ai、τi和fd,i分别表示基站i对应的回波信号的幅度、时延和多普勒频移;n(t)表示接收到的噪声。
利用确定的伪随机(PN)序列自相关函数大于一个码片时很小的特点,对采样所得到的数据进行广义相关。即
fi(τ,fd)=F-1{F(y(t))·
t∈(0,Tr)
(2)
式中:F[·]和F-1[·]分别表示傅里叶变换和逆傅里叶变换;Tr表示采样的信号长度; [·]*表示共轭。fd的取值范围由目标的最大运动速度所决定[4]。搜索fi(τ,fd)的峰值,即可得到一组峰值,而这些峰值映射在τ轴的值即为回波信号对应的时延,映射在fd轴的值则为回波信号对应的多普勒频移。然而由于CDMA各基站的导频序列与其他基站的导频序列相差64个码片的整数倍,这就导致如果两个基站间的偏移指数差小于M/(64*nc)时(其中,M为采样码片总数,nc为每个码片的采样数),直接利用模糊函数所得到的时延估计,既可能是该基站本身对应的时延,也可能是其他基站对应的时延,即不能有效地将基站与时延之间进行配对。
假设基站i的偏移指数为pi,那么利用基站i的导频信号与基站j的目标回波信号进行相干积累得到的峰值点为
τi,j=mod(τj+64·nc·(pi-pj)+M,M)
(3)
式中mod(·)表示求余数。同时,对fi(τ,fd)(i=


将向量Ψm中的第j个元素Ψm,j代替式(3)中的τj,可以得到新向量ξi,m.并且,其第j个元素为
ξi,m,j= mod(Ψm,j+64·nc·(pi-pj)+
M,M)
(4)
构造函数
(5)
基于以上分析,为了保证配对的准确性,可求得各基站对应的时延向量为
(6)
即可完成时延与基站之间的配对。
2 减小NLOS误差影响算法
2.1 定位模型分析

=Ri-Rj≜‖x-Xi‖-‖x-Xj‖
(7)
式中:Ri=‖x-Xi‖和Rj=‖x-Xj‖分别表示从目标到基站i和基站j的距离;c为电磁波在空气中的传播速度; 符号“*”表示没有噪声时的实际值。
在考虑噪声的情况下
(8)
式中,ni,1和di,1分别表示测量误差和NLOS误差。

(9)
式中:
Ψ=B(n+d)+0.5(n+d)⊗(n+d);
Ψ≈B(n+d)
(10)
利用式(6)和式(9)可得到
(11)
若不考虑NLOS误差影响,直接利用最小加权二乘(WLS)算法进行估计,得到目标位置初步估计结果:
(12)
式中,[·]-1表示矩阵的逆;
Ψ=BQB
(13)
Q为测量误差n的协方差矩阵。由WLS求解的性质,可知
(14)

(15)
(16)
式中:r=B-1h;H=B-1Ga.
(17)

(18)
(19)
同时
(20)
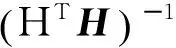
定义基于假定NLOS基站的方差函数

=E[nTRTRn]+E[(d-
(21)
(22)
分析式(22)可得到以下结论:

3) 由式(21)定义的基于假定NLOS基站的方差函数与文献[12]中定义的残差函数具有类似的效果,即估计的目标位置结果越准确,式(21)所定义的方差函数值将越小。因此,可利用加权平均办法,对于函数值大的目标位置估计结果赋予较小的权重,而函数值小的目标位置估计结果则赋予较大的权重,从而减小NLOS对定位结果的影响,获得较高的定位精度。
2.2 利用加权平均估计目标位置
按照以上三个结论,提出一种新的算法,如下:

(23)
(24)
(25)

2.3 结合Taylor级数展开
如果检测出的NLOS路径数l不大于N-3,就可利用Taylor级数展开来对NLOS误差值进行估计,并得到一个相对较好的目标位置估计值。方案如下:
利用式(25)所得值作为目标位置的初始值x(0)=[x(0),y(0)],对式(8)进行Taylor级数展开并忽略二阶以上项,可得到[14]
z=AΔ+d+n
(26)
式中:
新建一个(N-1)×l维矩阵C,并且其第i行第j列元素为
(27)
将A和C合并为一个新的矩阵D,即
D=[A|C]
(28)
设定基站集合所对应的NLOS误差矢量为dNLOS,那么式(26)可改写为
z=DΔd+n
(29)


(30)
在下次迭代中
x(0)=x(0)+Δ
(31)
仍然利用Taylor迭代的方法进行计算,直到Δx,Δy的值小于一个设定的门限:
|Δx|+|Δy|<ε
(32)
此时,停止迭代。结合Taylor级数展开算法的特性可以得知,如果检测的NLOS路径错误,那么通过计算式(30)得到的dNLOS中部分元素的值会很大。因此,若dNLOS中有元素的值大于设定的门限,则放弃式(31)所得到的结果,仍然利用加权平均的办法来实现对目标的定位。否则,式(25)计算得到的x(0)就是目标位置的估计值。
3 仿真分析
3.1 时延参数估计与基站配对
设有4个发射基站,呈正方形布站方式,坐标分别为[-9, 0] km,[0, 9] km,[9, 0] km,[0, -9]km,接收站坐标为[0, 0] km,各基站导频序列对应的偏移指数(64个码片的倍数)为0,4,8和12,各基站之间完全同步。目标位于[25, 20] km处,以300 m/s的速度沿x轴运动。基站2与目标之间存在NLOS路径。NLOS误差服从均值为500 m,均方差为500 m的高斯分布。
接收站所接收到的信号除目标回波信号之外,还包括各基站直达波信号和3条多径信号,且幅度衰落满足指数分布。每条直达波分量与噪声的干噪比为20 dB.同时,假设各基站对应的信噪比均为-14 dB,干信比均为20 dB.对接收信号进行混频滤波后,以5倍码片的速率采样,共采样5 000个数据(1 000个码片)。
结合文献[4]提出的级联对消方法,抑制接收信号中的干扰分量。然后利用基站1的导频信号与抑制后的接收信号进行广义相关,得到的模糊函数在时域的投影,如图2所示。可以看出:如果直接检测最大峰值所得到的时延,有可能是其他基站所对应的时延。所以必须要对其与基站进行配对。

图 2 基站1搜索结果在时域上的投影
为了验证所提算法的有效性,在不同的信噪比下进行1 000次蒙特卡罗仿真。并与直接检测算法、文献[4]中提出的“簇”算法检测失败概率进行了比较,如图3所示。由于文献[4]利用的是基站、目标和接收站位置之间的几何关系来自动配对时延和基站,当存在NLOS路径时,它们的几何关系将不再满足,而所提算法并不会受到几何关系的影响。因此,在NLOS环境下,所提算法能取得更优的配对性能。

图3 不同信噪比下三种检测算法的失败概率
3.2 NLOS抑制算法

噪声环境:在CDMA系统中,测量误差服从零均值的高斯分布,标准差为60 m,NLOS误差服从均值为500 m的高斯分布模型。
为了验证所提定位算法的有效性,将文献[12]提出的基于残差加权的定位算法与其进行比较。当基站2和基站3存在NLOS路径时,不同NLOS误差均方差情况下的定位均方根误差曲线如图4(a)所示。图4(b)为基站2、基站3和基站4存在NLOS路径时,不同均方差情况下的定位性能曲线。从图4(a)和图4(b)中可以看出当存在NLOS误差时,与文献[12]算法相比,利用所提算法可以取得更高的定位精度。

(a) 两个基站存在NLOS路径

(b) 三个基站存在NLOS路径图4 不同NLOS误差条件下定位性能比较
为了验证所提算法中结合Taylor级数展开情况下的定位性能,在第一种配置条件下进行了仿真,结果如图5所示。结果表明结合Taylor级数展开可以得到更高的定位精度。另外,对NLOS路径检测成功的概率如图6所示。从中可以发现,当NLOS误差的均方差较小或NLOS基站较少时,可以采用所提算法对NLOS基站进行有效检测。

图5 是否结合Taylor级数展开时,定位性能比较

图6 对NLOS路径估计成功的概率
4 结 论
研究了面向CDMA蜂窝网的运动目标定位过程中的时延配对和NLOS误差抑制问题。针对直接利用CDMA导频信号与接收信号进行广义相关得到模糊函数的峰值既可能代表相应基站的时延,也有可能代表其他基站的时延这一问题,提出了一种基于移位配准的配对办法,遍历搜索所有可能性,有效完成了对时延的估计和基站的配对。另一方面,针对定位中常见的NLOS误差抑制问题,提出了一种基于假定NLOS基站的方差函数,并结合加权平均的办法,充分利用NLOS基站的每一种可能性,可以有效减小NLOS误差的影响。另外,当根据所提方差函数检测出的NLOS基站较少时,利用检测得到的NLOS路径,结合Taylor级数展开算法,可以进一步提高对目标的定位精度。
[1] 曹轶超, 方建安, 罗贤云. 一个基于TDOA的无线定位新算法[J]. 电波科学学报, 2008, 23(5): 841-846.
CAO Yichao, FANG Jianan, LUO Xianyun. Constrained least-squares and wireless location based on TDOA measurements[J]. Chinese Journal of Radio Science, 2008, 23(5): 841-846. (in Chinese)
[2] 华树钢, 王 俊. 利用CDMA信号为照射源的雷达目标探测技术[J]. 系统工程与电子技术, 2009, 31(2): 337-341.
HUA Shugang, WANG Jun. Radar target detection using CDMA signals as illuminators[J]. Systems Engineering and Electronic, 2009, 31(2): 337-341. (in Chinese)
[3] 华 云, 龚耀寰. 利用CDMA 系统下行链路信号进行移动台定位的研究[J]. 电波科学学报, 2002, 17(5): 517-523.
HUA Yun, GONG Yaohuan. Using downlink signal to locate mobile station in CDMA systems[J]. Chinese Journal of Radio Science, 2002, 17(5): 517-523. (in Chinese)
[4] 田孝华, 廖桂生, 王洪洋. 基于CDMA蜂窝网的运动目标检测与定位技术[J]. 电波科学学报, 2005, 20(3): 336-341.
TIAN Xiaohua, LIAO Guisheng, WANG Hongyang. Moving target detection and location methods based on CDMA cellular networks[J]. Chinese Journal of Radio Science, 2005, 20(3): 336-341.(in Chinese)
[5] 柯 炜, 吴乐南. 基于非视距误差直接估计的定位跟踪算法[J]. 信号处理, 2010, 26(12): 1858-1863.
KE Wei, WU Lenan. Location tracking algorithm based on direct NLOS error estimation[J]. Signal Processing, 2010, 26(12): 1858-1863. (in Chinese)
[6] JIN I K, JANG G L, CHAN G P. A mitigation of line-of-sight by TDOA error modeling in wireless communication system[C]//International Conference on Control, Automatic and Systems 2008. Seoul, 2008: 1601-1605.
[7] WANN C D, HSUEH C S. NLOS mitigation with biased Kalman filters for range estimation in UWB systems[C]//IEEE TENCON 2007. Taipei, 2007: 1-4.
[8] JIANG Hao, XU Jie, LI Zhen. NLOS mitigation method for TDOA measurement[C]//2010 Sixth International Conference on Intelligent Information Hiding and Multimedia Signal Processing. Darmstadt, 2010: 196-199.
[9] 周康磊, 毛永毅. 基于残差加权的Taylor级数展开TDOA无线定位算法[J]. 西安邮电学院学报, 2010, 15(3): 10-13.
ZHOU Kanglei, MAO Yongyi. A TDOA location algorithm of Taylor series expansion based on rwg[J]. Journal of Xi’an University of Posts and Telecommunications, 2010, 15(3): 10-13. (in Chinese)
[10] CIURANA M, BARCELO-ARROYO F, CUGNO S. Tracking mobile targets indoors using WLAN and time-of-arrival[J]. Computer Communications, 2009, 32: 1552-1558.
[11] CHEN P C. A non-line-of-sight error mitigation algorithm in location estimation[C]//IEEE Wireless Communications Networking Conference.LA, USA 1999: 316-320.
[12] 倪建军, 李道本, 范跃祖. 一种CDMA蜂窝定位中减小NLOS误差的算法[J]. 电路与系统学报, 2005, 10(3):10-15.
NI Jianjun, LI Daoben, FAN Yuezu. A NLOS error mitigation algorithm for location in CDMA cellular networks[J]. Journal of Circuits and Systems, 2005, 10(3):10-15. (in Chinese)
[13] CHAN Y T, HO K C. A simple and efficient estimator for hyperbolic location[J]. IEEE Transactions on Signal Processing, 1994, 42(8): 1905-1915.
[14] FOY W H. Position-location solutions by Taylor-series estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 1976, 12(2): 187-194.

