运用矩阵束方法稀布优化可分离分布的平面阵

陈客松 郑美燕 刘卫东 吴宏刚 刘先攀

(1.电子科技大学电子工程学院，四川 成都 611731；2.中国民用航空局第二研究所，四川 成都 610041；电子科技大学航空航天学院，四川 成都 611731)

引 言

使用非均匀分布的平面阵来减少满足辐射方向图所需要的阵元数目一直是阵列天线系统设计的重要问题。阵元数目的减少在实际应用中有非常重要的意义，譬如卫星通信对天线的重量有限制，希望使用尽可能少的阵元。并且阵元的减少可以显著降低成本、简化天线系统。

综合平面阵列的阵元激励是一个线性问题，然而综合阵元位置和相位是一个包含多个未知量的高度非线性优化问题。传统的阵列综合技术如道尔顿-切比雪夫方法和泰勒方法[1-2]，仅可以综合均匀间隔的非均匀激励分布。它们在综合窄波束、低副瓣天线阵方面有良好的特性，但是由于均匀间距的限制，这些方法为得到所需的辐射特性可能需要更多的阵元数目。非均匀分布的阵列综合使得设计者有更大的自由度来减少阵元数目[3]。

目前已经有许多用来综合非均匀平面阵列的技术，包括优化算法(如遗传算法(GA)[4]、微分进化算法(DEA)[5]、免疫演算法[6]、解析方法[7-8]、动态规划法、粒子群优化方法(PSO))和其他综合技术等。其中，GA、DEA和PSO适合求解全局最优解，但是非常耗时；而其他许多基于迭代的方法往往难以保证找到所有变量的全局最优解。

矩阵束方法(MPM)[9-10]已成功应用于一维线性阵列的综合[11]。目前还未见将矩阵束方法应用到平面阵列综合中的报道。矩形平面阵列可分为可分离型分布平面阵和不可分离型分布平面阵。本文主要研究将矩阵束方法应用到可分离型分布的阵列中。如果一个矩形平面阵的激励分布是可分离的，则它所产生的方向图等于两个线阵方向图的乘积。首先对形成期望方向图的两个正交线阵进行均匀采样并由采样点数据构造Hankel矩阵；然后对此Hankel矩阵进行奇异值分解，在误差允许范围内求得逼近期望方向图所需的最小阵元数目；最后基于特征值分解的最小二乘准则计算两稀布线阵的阵元位置和激励，从而求得重构平面阵的阵元位置和激励。最后的仿真实验将会优化切比雪夫平面阵列(非等激励)的方向图和优化经免疫演算法[6](非均匀阵元位置和非等激励)稀布后的方向图，并将其与文献[12]的稀布约束最优化方法进行比较。

1 MPM用于稀布可分离型平面阵

1.1 阵列的最优化模型

矩形平面阵列结构如图1，其单元按矩形栅格排列在xoy平面上。此阵在沿x轴方向上M行阵元，行间距为dx，沿y轴方向上有N列阵元，列间距为dy，共有M×N个阵元，任一阵元编号为(m,n)。假设阵元均为全向辐射元。

图1 平面阵列模型

则矩形栅格平面阵的方向图可写为

(1)

式中：k=2π/λ，λ为工作波长；u=sinθcosφ，v=sinθsinφ. 0≤θ≤π，0≤φ≤2π分别表示方位角和俯仰角。dx和dy分别为第(m,n)阵元的横坐标和纵坐标。

若此阵列为可分离型分布，方向图可以表示为[13]

F(θ,φ)=Fx(θ,φ)Fy(θ,φ)

(2)

其中

(3)

(4)

式中，Rm和Rn分别为与x轴平行的列和与y轴平行的行中阵元的归一化电流。

可知在激励分布为可分离型分布的条件下，具有矩形边界的矩形栅格阵列的方向图是沿x轴排列的线阵X和沿y轴排列的线阵Y的方向图的乘积。

矩阵束方法(MPM)是在误差允许范围内，使用尽可能少的阵元形成新的可分离型平面阵列来逼近期望的方向图。最优化问题的数学描述

(5)

1.2 矩阵束方法估计最小阵元数目

对期望方向图从u=-1到u=1进行均匀采样[12]，即对XOZ面的方向图进行采样，则us=sΔ=s/S，其中s=-S,…,0,…,S,有(2S+1)个采样点。同理，对期望方向图从v=-1到v=1进行均匀采样[12]，即对YOZ面的方向图进行采样，则vt=t=t/T，其中t=-T,…,0,…,T.有(2T+1)个采样点。任一采样点(s,t)处的值为

fM,N(s,t) =fM(s)fN(t)

(6)

式中，zm=ejωmΔ=ejkmdxΔ,zn=ejωn=ejkndy.根据Nyquist采样定理，必须满足条件Δ()≤λ/2dmax,其中dmax=max{dm(dn)}.线阵X上(2S+1)、线阵Y上(2T+1)个采样点足以描述线阵X上M个、线阵Y上N个单元均匀分布的阵列的方向图。

由期望方向图的采样数据构造一种特殊的矩阵-Hankel矩阵。由线阵X上的(2S+1)个采样点数据构造Hankel矩阵，得到

(7)

式中，y(s)=fM(s-S).参数{S,L}的选择必须满足条件2S-L≥M,L+1≥M.如文献[9]、[10]所述，可以假设S=L=M，可以使用最少的采样点保持最好的方向图特性。由式(7)可以看出，虽然L的值远小于采样点数，但(2S+1)个采样点全部用到。

对矩阵Y进行奇异值分解(SVD)，表达式为

Y=UΣVH

(8)

其中：U∈C(2S-L+1)×(2S-L+1),V∈C(L+1)×(L+1)为酉矩阵，分别为YYH和YHY的特征向量； {σi}是Y的奇异值，Σ=diag{σ1,σ2,…,σM,…,σW;σ1≥σ2≥…≥σW},W=min{2M-L+1，L+1}.

Hankel矩阵Y的秩等于非零奇异值的数目，一般，由M个阵元组成的阵列则有M个非零奇异值。然而，文献[11]的结果表明，对许多要设计的天线阵列，重要奇异值的数目要远小于总的阵元数，也就是说那些不重要的阵元的贡献可以由其他阵元的组合代替。因此，可以舍弃那些不重要的奇异值来获得矩阵Y的近似低秩矩阵，这个近似矩阵对应着更少阵元组成的新阵列。通常的处理方法是将这些小的奇异值设为0.即

YQ=UΣQVH

(9)

其中,ΣQ=diag{σ1,σ2,…,σQ,0,…,0},Q≤M.对所有的秩为Q的矩阵中，YQ的Frobenius范数逼近误差最小，即

(10)

由式(10)可以看出近似误差随着阵元数目Q的增加单调地减小，当Q=M时误差为0.这说明稀布后的阵列总能很好地逼近期望方向图。

在实际的阵列综合问题中，Q的最小值可以通过下式确定

(11)

式中，ε是一个很小的正数，ε的选择取决于重构方向图和原方向图的逼近程度。

按上述方法由线阵Y上的2T+1个采样点数据可以求得优化后所需最小阵元数目P.

1.3 矩阵束方法求解稀布后两垂直线阵的阵元位置和激励

阵元位置和激励可通过求解矩阵的广义特征值确定，首先求解线阵X，由矩阵V的前Q列构造矩阵V′，

V′=[v1,v2,…,vQ]

(12)

根据式(8)，可以得到

(13)

(14)

(15)

等效于求解下列矩阵的特征值

(16)

(17)

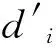
(18)

(19)

(20)

则阵元激励的计算为

(21)

式中：

(22)

(23)

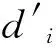
同样的方法求解线阵Y的阵元位置和激励。

2 仿真实例

例1：综合可分离型切比雪夫平面阵

假设一20×20的切比雪夫平面阵，即M=20,N=20，阵元间距dx=dy=λ/2.副瓣电平SLL=-30 dB.设计一非均匀可分离型平面阵列，使其阵元数目小于均匀切比雪夫阵列所需的阵元数目。在此例中，采样参数设置为S=M,T=N(进一步增加采样点也不会改善方向图逼近精度)。根据式(8),当ε=10-2所需的最小阵元数目为Q=12,P=12；当ε=10-3所需的最小阵元数目为Q=13,P=13.图2是Q=12,P=12的重构方向图及期望方向图，所求得的副瓣电平为SLL1=-29.037 2 dB.图3分别对比了Q=12,P=12和Q=13,P=13的重构方向图及期望方向图的切面图。由图可见，Q=13,P=13不等间距分布的阵元在精度ε=10-3下可以精确重构M=20,N=20等间距分布的阵元才能产生的切比雪夫方向图，所求得的副瓣电平为SLL2=-29.948 9 dB.此例分别节省64%和57.75%的阵元。尽管基于矩阵束的方法并未限制激励的分布形式，但在这个例子中由于方向图的对称性导致阵元激励是对称分布的。表1列出了切比雪夫阵列阵元的激励及Q=12,P=12和Q=13,P=13时阵元的位置和激励。第(m,n)个阵元的位置为(dm,dn)，激励为Rm,n=Rm×Rn.图4是均匀分布的阵元位置和稀布后阵元位置。阵元是对称分布的，因此只给出第一象限的阵元位置和激励以及阵元位置图。观察可知，重构阵列的孔径小于切比雪夫阵列的孔径。

图3 重构阵列及期望阵列方向图的切面图

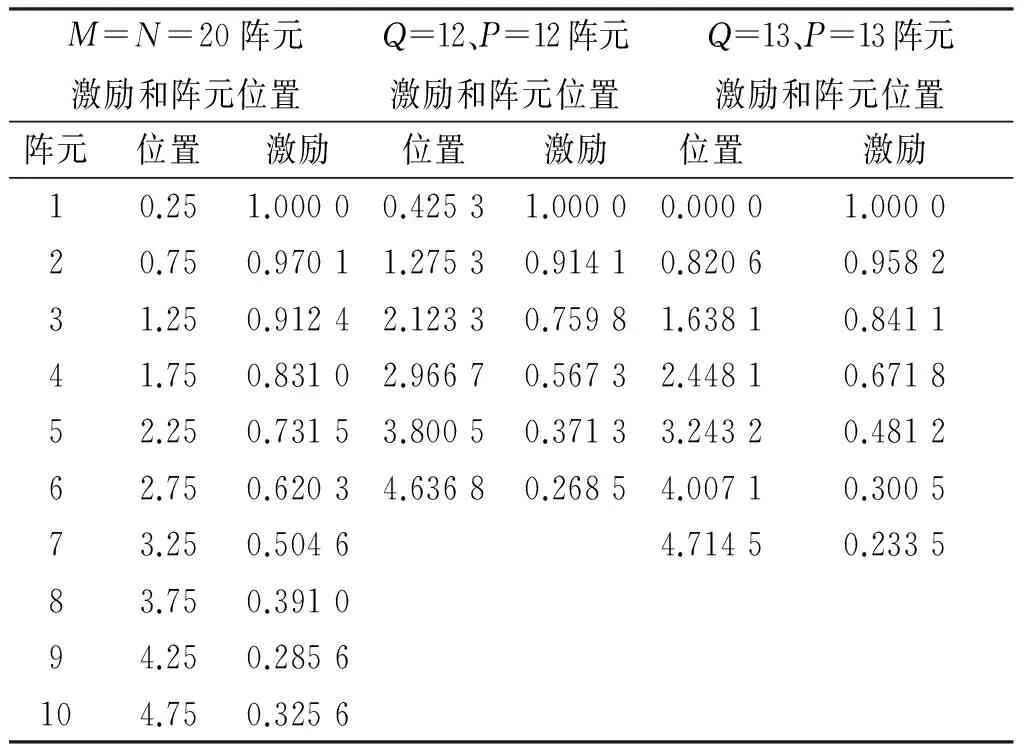
表1 均匀分布的阵元激励及重构阵列阵元激励和位置

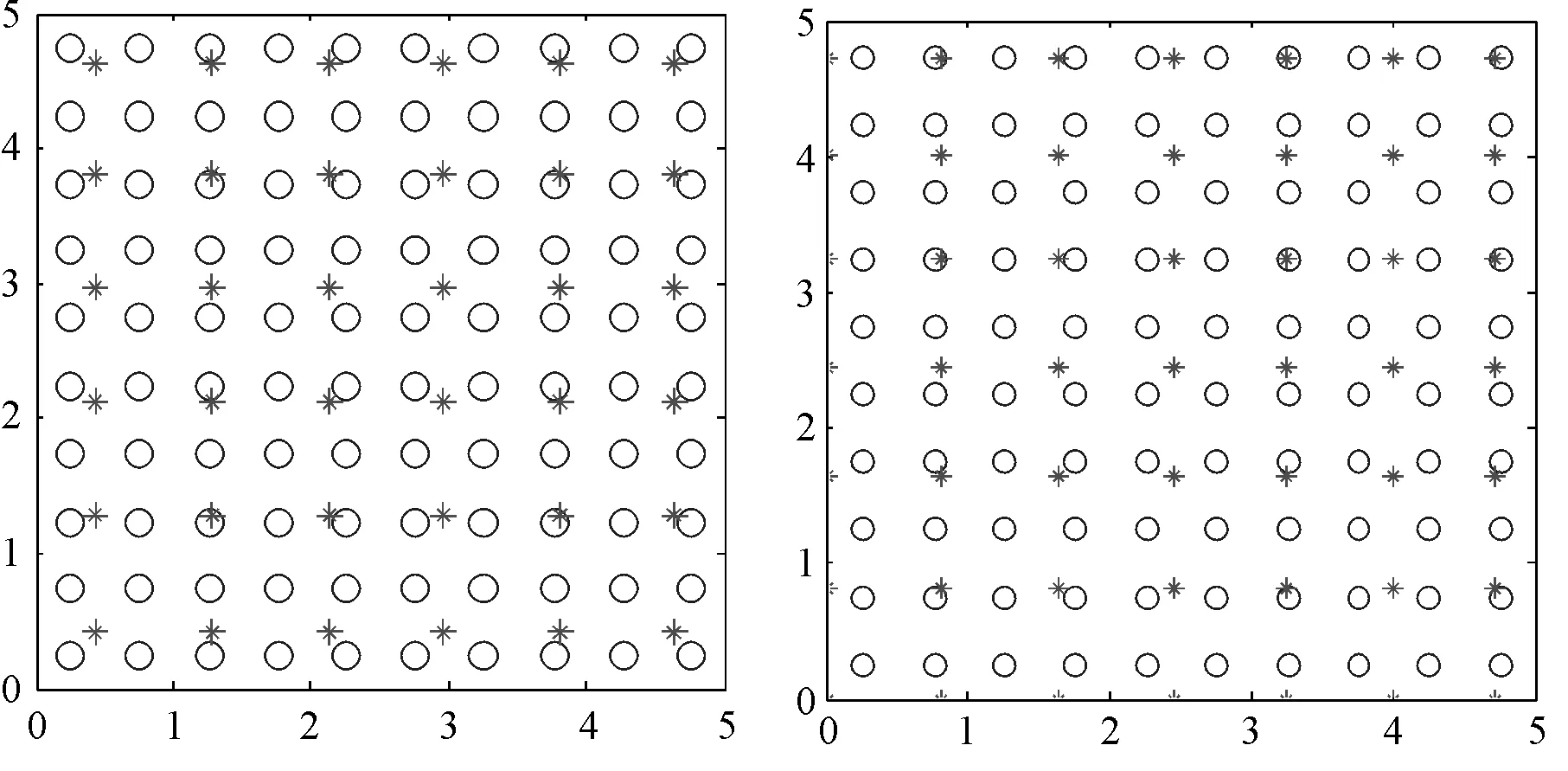
O均匀阵元*稀布后阵元O均匀阵元*稀布后阵元图4 均匀分布的阵元位置和稀布后的阵元位置

例2 ：非均匀分布的平面阵列的优化

为说明MPM的有效性，将文献[6]的数据作为输入来综合方向图。此可分离型阵列由32×32个阵元组成，即M=32,N=32，阵元位置和激励如表2所示。文献[12]采用稀疏约束优化方法对此平面阵优化，此例采用矩阵束方法对此阵列优化，并与文献[12]的结果进行比较。在本例中，采样参数设为S=M,T=N.根据式(8),当ε=10-6所需的最小阵元

数目为Q=19,P=19.图5是Q=19,P=19的重构方向及文献[6]方向图。图6对比了Q=19,P=19的重构方向图及文献[6]的方向图的切面图。由图可见，应用矩阵束方法只需Q=19,P=19个阵元，便可以精确重构应用免疫演算法需要M=32,N=32个阵元才能产生的方向图。此例节省65%阵元。应用文献[12]的疏约束优化方法采用496个阵元去逼近期望方向图，可节省51%阵元。将图6和文献[12]的图8比较可得，应用矩阵束方法的逼近精度比稀疏优化约束方法要高。可知，矩阵束方法的性能要优于文献[12]的稀疏约束优化方法。表2列出了文献[6]中的阵元位置和激励以及重构方向图的阵元位置和激励。第(m,n)个阵元的位置为(dm,dn)，激励为Rm,n=Rm×Rn.图7是文献[6]和重构方向图的阵元位置图。因阵元是对称分布的，只给出了第一象限的阵元位置和激励以及阵元位置图。

图6 文献[6]和重构阵列的切面图

图7 阵元位置图

文献[6]的阵元位置/激励稀布后的位置/激励阵元位置激励位置激励10.26041.00000.00001.000020.79951.00000.85960.978131.22480.55641.71980.906941.62610.96802.58230.799452.23620.99123.44740.665762.80050.55074.31510.519972.87900.26165.18570.376783.34710.60706.05850.249093.80410.56606.93320.1471104.29940.08207.80970.0855114.39240.5090124.89130.3156135.38750.4293146.14230.3605156.97220.2263167.82370.1362

3 结 论

提出了一种基于矩阵束方法(MPM)的可分离型分布平面阵列的稀布综合法，与基于随机优化的算法相比，基于矩阵束的方法是一种非迭代算法，它适合于要求窄波束、低副瓣的稀布阵列优化设计问题；另外，矩阵束方法不需要计算数据的相关系数矩阵，因此,计算量小。文中给出的可分离型分布阵列综合未考虑阵元之间的互耦，实际的阵元间因存在互耦，使得各单元具有不同的方向图。所以，在非互耦的情况下得到的阵列综合结果，一般可以通过对阵元激励和位置分布进行微调来解决。 如何同时进行互耦校正的可分离型平面阵列稀布综合问题，可以在参考阵列综合领域中的文献[15]的基础上，开展进一步的研究。

[1] BALANISC A.Antenna Theory:Analysis and Designed[M].3rd ed.New York:Wiley,2005.

[2] ORFANIDISS J.Electromagnetic Waves and antenna [M/OL].[2010-02-26].http://www.ece.rutgers.edu/～orfanidi/ewa/.

[3] LOY T,LEE W.A study of spaced-tapered arrays[J].IEEE Trans Antenna Propag,1966,14(1):22-30.

[4] 陈客松,何子述.平面稀布天线阵列的优化算法[J].电波科学学报,2009,24(2):193-198.

CHEN Kesong,HE Zishu.Synthesis approach for sparse plane arrays[J].Chinese Journal of Radio Science,2009,24(2):193-198.(in Chinese)

[5] KURUPD G,HIMDI M.Synthesis of uniform amplitude unequally spaced antenna arrays using the differential evolution algorithm[J].IEEE Trans on Antenna and Propagation,2003,51(9):2210-2217.

[6] YE Jianfeng,PANG Weizheng.Immune algorithm in array pattern synthesis with side lobe reduction[C]//IEEE International Conference on Microwave and Millimeter Wave Technology.Nanjing,April 21-24,2008:1127-1130.

[7] 柴焱杰,孙继银.平面波在时域有限差分法中的引入方法研究[J].电波科学学报,2011,26(2):388-392.

CAI Yanjie,SUN Jiyin.Importing methods of plane wave in the finite difference time domain method[J].Chinese Journal of Radio Science,2011,26(2):388-392.(in Chinese)

[8] KUMAR B P,BRANNER G R.Generalized analytical technique for the synthesis of unequally spaced arrays with linear,planar,cylindrical or spherical geometry[J].IEEE Trans on Antennas and Propagation,2005,53(2):621-633.

[9] SAPKAR T K,PEREIRA O.Using the matrix pencil method to estimate the parameters of a sum of complex exponentials[J].IEEE Antennas and Propagation Magazine,1995,37(1):48-54.

[10] HUA Yingbo,SAPKAR T K.Matrix pencil method for estimating parameters of exponentially damped/undamped sinusoids in noise[J].IEEE Trans on Acoustics Speech and Signal Processing,1990,38(5):814-824.

[11] LIU Yanhui,NIE Zaiping,LIU Qinghuo.Reducing the number of elements in a linear antenna array by the matrix pencil method[J].IEEE Trans on Antennas and Propagation,2008,56(9):2955-2962.

[12] ZHANG Wenji,LI Lian,LI Fang.Reducing the number of elements in linear and planar antenna arrays with sparseness constrained optimization[J].IEEE Trans on Antennas and Propagation,2011,59(8):3106-3111.

[13] 薛正辉,李伟明,任 伍.阵列天线分析与综合[M].北京:北京航空航天大学出版社,2011:261-265.

[14] MILLER E K,GOODMAN D M.A pole-zero modeling approach to linear array synthesis I:the unconstrained solution[J].Radio Science,1983,18(1):57-69.doi:10.1029/RS018i001p00057.

[15] 闫玉波,崔玉国,焦培南.基于副瓣峰值控制的天线阵方向图综合[J].电波科学学报,2009,24(2):249-253.

YAN Yubo,CUI Yuguo,JIAO Peinan.Pattern Synthesis of antenna arrays based on control of peak sidelobes[J].Chinese Journal of Radio Science,2009,24(2):249-253.(in Chinese)